Uso De La Tabla De La Distribucion Normal Z 191k17
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Uso De La Tabla De La Distribucion Normal Z as PDF for free.
More details 6z3438
- Words: 930
- Pages: 4
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE CIENCIAS QUIMICAS Y FARMACIA UNIDAD DE INFORMATICA ESTADISTICA USO DE LA TABLA PARA LA DISTRIBUCION NORMAL Si la frecuencia de ocurrencia de una variable continua se representa en un histograma, se tendría en el eje “x” los valores de dicha variable en forma de intervalos de clase, pero que representan una serie continua de valores, es decir que los intervalos están uno seguido del otro y en ese eje pueden estar infinitos valores. En el eje “y” se representan las frecuencias por medio de las barras o columnas del histograma; por lo tanto, si se tienen frecuencias relativas de ocurrencia de la variable según los intervalos de clase, ésta es una representación de una distribución de probabilidad; como por ejemplo el siguiente histograma de la frecuencia relativa de notas en un examen: .4
Fraction
.3
.2
.1
0 20
40
60 NOTA
80
100
La mayoría de variables continuas tienen un comportamiento en forma de campana más o menos simétrica cuando se representan como histogramas o diagramas de tallo y hoja; lo que se denomina una distribución “normal”. Para poder describir la distribución de probabilidad de cualquier variable continua que tenga este comportamiento, la función de densidad está dada por la fórmula:
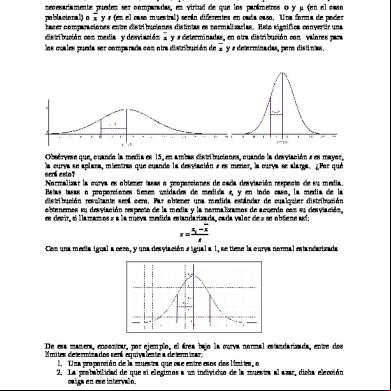
Nótese que los parámetros de la distribución corresponden a los valores que puede adquirir “y” con base a la media aritmética y la desviación estándar de la población, pero para que pueda aplicarse a cualquier variable, la distribución se calcula con base a una variable estándar denominada “Z”, cuya expresión es:
Esta variable Z, tiene como característica que su media poblacional ( ) es igual a 0, y la desviación estándar ( ) es igual a 1 y no tiene dimensionales. La distribución de densidad de la variable Z, así como la de cualquier variable continua, es infinitamente pequeña; imagínese en el histograma, la porción de área que le correspondería a la probabilidad de tener una nota exactamente igual a 61 puntos, sin contar que entre dos notas enteras hay infinitos decimales, que a su vez contribuyen con una parte de área, la cual cuando se observa el intervalo es ya considerable, pero deriva del aporte de probabilidad de cada posible valor. Es por eso, que la función que se utiliza en la práctica es la función acumulada, de acuerdo a la siguiente fórmula:
Como se puede ver, los límites van desde menos a más infinito para la variable “Z”, lo que quiere decir que la función de probabilidad acumulada de la variable describe una campana simétrica y asintótica con centro en la media aritmética 0 y área total igual a 1.0000, el área debajo de la curva se interpreta como probabilidad acumulada entre dos valores de Z. Los valores por debajo de la media son negativos (-Z) y los valores por arriba de la media son positivos (+Z).
1.
Partes de la tabla
1.1
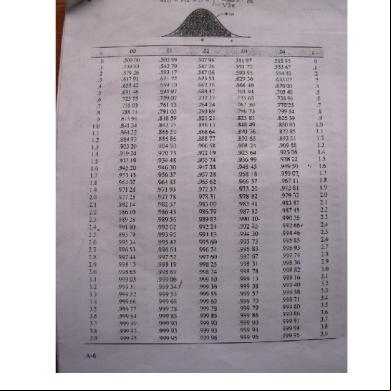
En la primera columna se encuentra el valor Z deseado con una cifra para los enteros (entre 0 y 3) y una cifra significativa para el primer decimal (entre 0.0 y 0.9).
1.2 1.3
En las siguientes columnas, se debe ubicar la cifra significativa para el segundo decimal (entre 0.00 y 0.09). En las filas se encuentra la probabilidad acumulada entre Z=0 y Z (según se esquematiza en la figura anterior).
2.
Uso de la tabla
2.1
Debe tomarse en cuenta, que la tabla proporcionada corresponde al área de la mitad de la distribución, por lo que el área entre 0 y más infinito es 0.5000. La probabilidad para valores inferiores a 0 (valores de Z negativos), es exactamente la misma que para valores superiores a 0 (valores de Z positivos), por lo que la tabla puede servir para ambos casos. Si se desea determinar un valor específico de probabilidad, debe ubicarse en la gráfica qué porción de área se pide, y aplicar las operaciones matemáticas de suma o resta, según los casos que se verán en clase. La tabla puede utilizarse a la inversa, es decir, si se tiene una probabilidad dada, se pueden establecer los valores Z que la limitan, realizando el procedimiento inverso.
2.2
2.3
2.4
3.
Estandarización de variables continuas
Como se indicó anteriormente, cualquier variable continua puede transformarse o convertirse a una variable Z y calcular diferentes probabilidades. También puede aplicarse la regla inversa del uso de la tabla y determinar qué valores de la variable delimitan cierta probabilidad. Los casos que se tienen para calcular probabilidades o valores son: 3.1
Estudio de una población En este caso, se tiene el total de datos poblacionales, se calcula su media aritmética ( ) y desviación estándar ( ), se pueden calcular las probabilidades en función de valores que pueda adquirir la variable “y” de la población:
3.2
Estudio de una muestra Cuando se tiene una muestra y se calcula su media () y su desviación estándar (s), se pueden calcular las probabilidades en función de valores que pueda adquirir la variable “y” de la muestra:
3.3
Estudio de la media aritmética obtenida de una muestra Cuando se tiene una muestra de tamaño “n” estadísticamente representativa de la población, se pueden calcular las probabilidades sobre la media aritmética de la población con base en los valores “” que podría adquirir la muestra. En este caso, se debe tener conocimiento del valor de la media poblacional ( ) y de la desviación estándar poblacional ( ), y con ésta última, se puede determinar el denominado “error estándar”, que sería la desviación estándar de la media cuando se tiene una muestra de tamaño “n”:
Fraction
.3
.2
.1
0 20
40
60 NOTA
80
100
La mayoría de variables continuas tienen un comportamiento en forma de campana más o menos simétrica cuando se representan como histogramas o diagramas de tallo y hoja; lo que se denomina una distribución “normal”. Para poder describir la distribución de probabilidad de cualquier variable continua que tenga este comportamiento, la función de densidad está dada por la fórmula:
Nótese que los parámetros de la distribución corresponden a los valores que puede adquirir “y” con base a la media aritmética y la desviación estándar de la población, pero para que pueda aplicarse a cualquier variable, la distribución se calcula con base a una variable estándar denominada “Z”, cuya expresión es:
Esta variable Z, tiene como característica que su media poblacional ( ) es igual a 0, y la desviación estándar ( ) es igual a 1 y no tiene dimensionales. La distribución de densidad de la variable Z, así como la de cualquier variable continua, es infinitamente pequeña; imagínese en el histograma, la porción de área que le correspondería a la probabilidad de tener una nota exactamente igual a 61 puntos, sin contar que entre dos notas enteras hay infinitos decimales, que a su vez contribuyen con una parte de área, la cual cuando se observa el intervalo es ya considerable, pero deriva del aporte de probabilidad de cada posible valor. Es por eso, que la función que se utiliza en la práctica es la función acumulada, de acuerdo a la siguiente fórmula:
Como se puede ver, los límites van desde menos a más infinito para la variable “Z”, lo que quiere decir que la función de probabilidad acumulada de la variable describe una campana simétrica y asintótica con centro en la media aritmética 0 y área total igual a 1.0000, el área debajo de la curva se interpreta como probabilidad acumulada entre dos valores de Z. Los valores por debajo de la media son negativos (-Z) y los valores por arriba de la media son positivos (+Z).
1.
Partes de la tabla
1.1
En la primera columna se encuentra el valor Z deseado con una cifra para los enteros (entre 0 y 3) y una cifra significativa para el primer decimal (entre 0.0 y 0.9).
1.2 1.3
En las siguientes columnas, se debe ubicar la cifra significativa para el segundo decimal (entre 0.00 y 0.09). En las filas se encuentra la probabilidad acumulada entre Z=0 y Z (según se esquematiza en la figura anterior).
2.
Uso de la tabla
2.1
Debe tomarse en cuenta, que la tabla proporcionada corresponde al área de la mitad de la distribución, por lo que el área entre 0 y más infinito es 0.5000. La probabilidad para valores inferiores a 0 (valores de Z negativos), es exactamente la misma que para valores superiores a 0 (valores de Z positivos), por lo que la tabla puede servir para ambos casos. Si se desea determinar un valor específico de probabilidad, debe ubicarse en la gráfica qué porción de área se pide, y aplicar las operaciones matemáticas de suma o resta, según los casos que se verán en clase. La tabla puede utilizarse a la inversa, es decir, si se tiene una probabilidad dada, se pueden establecer los valores Z que la limitan, realizando el procedimiento inverso.
2.2
2.3
2.4
3.
Estandarización de variables continuas
Como se indicó anteriormente, cualquier variable continua puede transformarse o convertirse a una variable Z y calcular diferentes probabilidades. También puede aplicarse la regla inversa del uso de la tabla y determinar qué valores de la variable delimitan cierta probabilidad. Los casos que se tienen para calcular probabilidades o valores son: 3.1
Estudio de una población En este caso, se tiene el total de datos poblacionales, se calcula su media aritmética ( ) y desviación estándar ( ), se pueden calcular las probabilidades en función de valores que pueda adquirir la variable “y” de la población:
3.2
Estudio de una muestra Cuando se tiene una muestra y se calcula su media () y su desviación estándar (s), se pueden calcular las probabilidades en función de valores que pueda adquirir la variable “y” de la muestra:
3.3
Estudio de la media aritmética obtenida de una muestra Cuando se tiene una muestra de tamaño “n” estadísticamente representativa de la población, se pueden calcular las probabilidades sobre la media aritmética de la población con base en los valores “” que podría adquirir la muestra. En este caso, se debe tener conocimiento del valor de la media poblacional ( ) y de la desviación estándar poblacional ( ), y con ésta última, se puede determinar el denominado “error estándar”, que sería la desviación estándar de la media cuando se tiene una muestra de tamaño “n”: