Uso De La Curva Normal 2j39f
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Uso De La Curva Normal as PDF for free.
More details 6z3438
- Words: 320
- Pages: 2
Uso de la curva normal Las distribuciones de frecuencia, aunque manifiesten un comportamiento normal, no necesariamente pueden ser comparadas, en virtud de que los parámetros σ y µ (en el caso poblacional) o x y s (en el caso muestral) serán diferentes en cada caso. Una forma de poder hacer comparaciones entre distribuciones distintas es normalizarlas. Esto significa convertir una distribución con media y desviación x y s determinadas, en otra distribución con valores para los cuales pueda ser comparada con otra distribución de x y s determinadas, pero distintas.
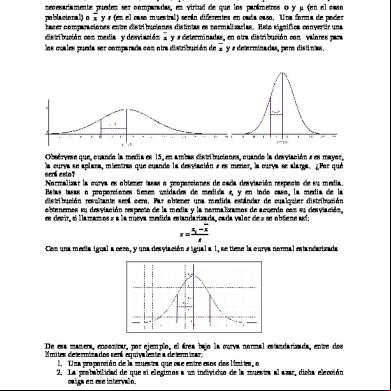
Obsérvese que, cuando la media es 15, en ambas distribuciones, cuando la desviación s es mayor, la curva se aplana, mientras que cuando la desviación s es menor, la curva se alarga. ¿Por qué será esto? Normalizar la curva es obtener tasas o proporciones de cada desviación respecto de su media. Estas tasas o proporciones tienen unidades de medida s, y en todo caso, la media de la distribución resultante será cero. Par obtener una medida estándar de cualquier distribución obtenemos su desviación respecto de la media y la normalizamos de acuerdo con su desviación, es decir, si llamamos z a la nueva medida estandarizada, cada valor de z se obtiene así: x x z i s Con una media igual a cero, y una desviación s igual a 1, se tiene la curva normal estandarizada
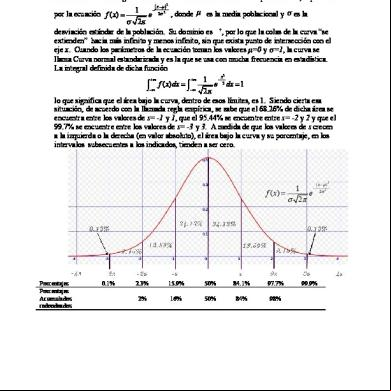
De esa manera, encontrar, por ejemplo, el área bajo la curva normal estandarizada, entre dos límites determinados será equivalente a determinar: 1. Una proporción de la muestra que cae entre esos dos límites, o 2. La probabilidad de que si elegimos a un individuo de la muestra al azar, dicha elección caiga en ese intervalo.
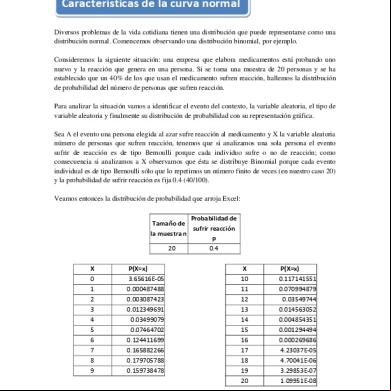
Para la determinación de esa área, no se pueden usar métodos tradicionales del cálculo integral. Por medio de métodos numéricos, existen tablas que proporcionan las tasas o proporciones correspondientes a cada valor z determinado. Luis Solórzano 01 agosto 2008
Obsérvese que, cuando la media es 15, en ambas distribuciones, cuando la desviación s es mayor, la curva se aplana, mientras que cuando la desviación s es menor, la curva se alarga. ¿Por qué será esto? Normalizar la curva es obtener tasas o proporciones de cada desviación respecto de su media. Estas tasas o proporciones tienen unidades de medida s, y en todo caso, la media de la distribución resultante será cero. Par obtener una medida estándar de cualquier distribución obtenemos su desviación respecto de la media y la normalizamos de acuerdo con su desviación, es decir, si llamamos z a la nueva medida estandarizada, cada valor de z se obtiene así: x x z i s Con una media igual a cero, y una desviación s igual a 1, se tiene la curva normal estandarizada
De esa manera, encontrar, por ejemplo, el área bajo la curva normal estandarizada, entre dos límites determinados será equivalente a determinar: 1. Una proporción de la muestra que cae entre esos dos límites, o 2. La probabilidad de que si elegimos a un individuo de la muestra al azar, dicha elección caiga en ese intervalo.
Para la determinación de esa área, no se pueden usar métodos tradicionales del cálculo integral. Por medio de métodos numéricos, existen tablas que proporcionan las tasas o proporciones correspondientes a cada valor z determinado. Luis Solórzano 01 agosto 2008