Curva Normal 40j4e

La curva normal La curva normal es la gráfica de la llamada función de densidad de probabilidad, expresada  x  2

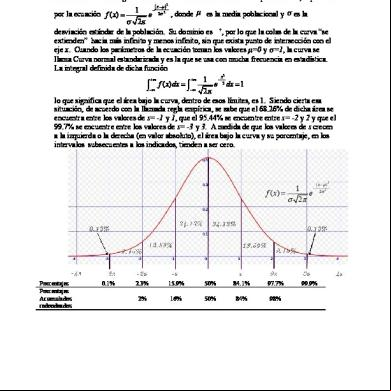
 1 2 por la ecuación f ( x)  e 2 , donde  es la media poblacional y  es la  2 desviación estándar de la población. Su dominio es +, por lo que la colas de la curva “se extienden” hacia más infinito y menos infinito, sin que exista punto de intersección con el eje x. Cuando los parámetros de la ecuación toman los valores =0 y =1, la curva se llama Curva normal estandarizada y es la que se usa con mucha frecuencia en estadística. La integral definida de dicha función 2   1  x2  f ( x)dx   2 e dx  1 lo que significa que el área bajo la curva, dentro de esos límites, es 1. Siendo cierta esa situación, de acuerdo con la llamada regla empírica, se sabe que el 68.26% de dicha área se encuentra entre los valores de s= -1 y 1, que el 95.44% se encuentre entre s= -2 y 2 y que el 99.7% se encuentre entre los valores de s= -3 y 3. A medida de que los valores de s crecen a la izquierda o la derecha (en valor absoluto), el área bajo la curva y su porcentaje, en los intervalos subsecuentes a los indicados, tienden a ser cero.

 1 f ( x)  e  2

Porcentajes Porcentajes Acumulados redondeados

0.1%

2.3%

15.9%

50%

84.1%

97.7%

2%

16%

50%

84%

98%

 x   2

99.9%

2 2