Dimensiones, Unidades Fundamentales Y Suplementarias Del Si 614b2x
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Dimensiones, Unidades Fundamentales Y Suplementarias Del Si as PDF for free.
More details 6z3438
- Words: 1,540
- Pages: 8
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” DIMENSIONES. La dimensión (del latín dimensio, "medida") es, esencialmente, el número de grados de libertad para realizar un movimiento en el espacio. Comúnmente, las dimensiones de un objeto son las medidas que definen su forma y tamaño. Medida de la longitud, ancho, o profundo; Tamaño o importancia de algo; Propiedad del espacio, extensión en alguna dirección. En las ciencias físicas y la ingeniería, del tamaño de una magnitud física es la expresión del tipo de unidades de medida en que esta cantidad se expresa. La dimensión de la velocidad, por ejemplo, resulta de dividir la longitud entre el tiempo. En el sistema SI, las dimensiones vienen dadas por siete magnitudes fundamentales relacionadas con las características físicas fundamentales. MAGNITUDES BASICAS Y DERIVADAS. La mayoría de las magnitudes físicas son magnitudes derivadas porque se derivan de otras. Directamente se derivan de aquellas en función de las cuales se definen por medio de ecuaciones matemáticas, tales como, las ecuaciones de definición de magnitudes o las que expresan leyes físicas. Por ejemplo, la densidad es una magnitud que se deriva de la masa y el volumen, como lo establece la ecuación que la define: p = m/V. La presión se deriva de la fuerza y del área sobre la cual actúa (ecuación de definición: p = F/A). La aceleración se deriva de la velocidad y el tiempo (ecuación de definición: a = dv/dt). etc. Existen, sin embargo, magnitudes que no se derivan de otras; son independientes entre sí y, por lo tanto, indefinibles en términos de otras. Son magnitudes primarias, básicas o fundamentales; y todas las magnitudes físicas se derivarían directa o indirectamente de ellas. En el Sistema Mecánico son tres: la longitud, la masa y el tiempo. En el Sistema Internacional son siete: la longitud, la masa, el tiempo, la corriente eléctrica, la temperatura termodinámica, la cantidad de substancia y la intensidad luminosa. Ver Tabla 1.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” LA DIMENSION FISICA DE UNA MAGNITUD Las magnitudes físicas pueden ser expresadas en términos de las magnitudes básicas de un sistema por medio de expresiones conocidas como dimensiones físicas, cuya importancia, en el marco de un enfoque riguroso de la ciencia, es de inapreciable valor. En este contexto, ha sido posible organizar sistemas dimensionales construidos sobre la base de un grupo de magnitudes, elegidas como magnitudes básicas o fundamentales, cuyas dimensiones serían las dimensiones básicas del sistema. En el Sistema Mecánico las dimensiones de las magnitudes básicas (dimensiones básicas), se representan por medio de las letras L, M y T para la longitud, la masa y el tiempo, respectivamente. En el Sistema Internacional, a las anteriores, se agregan las letras I, O, N y J para la corriente eléctrica, la temperatura termodinámica, la cantidad de substancia y la intensidad luminosa, respectivamente. Las dimensiones de una magnitud física Q cualquiera, en un sistema dado, quedará expresada por medio de un producto de potencias de las dimensiones básicas del sistema considerado Así, en los sistemas mecánico e internacional se tiene:
En donde los exponentes son los exponentes dimensionales cuyos valores, característicos para cada magnitud física, pueden ser mayores, iguales o menores que cero. Por ejemplo, para la energía molar se tiene:
En donde xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx considerando, que toda potencia de exponente cero es igual a 1.
y
Si todos los exponentes dimensionales de la magnitud Q fueran iguales a cero, su producto dimensional sería igual a 1:
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” En este caso, la magnitud física Q es adimensional. Ejemplos, la densidad relativa, la fracción molar, etc. La dimensión de una magnitud básica se tiene cuando el exponente dimensional de su dimensión básica es igual a 1, e igual a cero los exponentes de las otras dimensiones básicas. Por ejemplo:
Las dimensiones de las magnitudes derivadas se obtienen a partir de las ecuaciones matemáticas que las definen o de las que expresan leyes físicas. Por ejemplo:
Bibliografia: http://es.wikipedia.org/wiki/Dimensi%C3%B3n http://www.quimicabasica.cl/temas.htm
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” Puede apreciarse, que la dimensión física de una magnitud, en un sistema dado, nos informa sobre el cómo se halla relacionada o se deriva de las magnitudes básicas del sistema. Por ejemplo, la velocidad se deriva de la longitud y el tiempo, pues sus dimensiones LT-1 nos indica que es una longitud dividida por un tiempo. La fuerza se deriva de la longitud, la masa y el tiempo, pues sus dimensiones MLT-2 nos indica que es una masa por una longitud dividida por un tiempo al cuadrado. El empleo de un sistema dimensional nos permite, por una parte, identificar a las magnitudes físicas, considerando el hecho de que tienen diferentes dimensiones físicas. Por otra parte, exige que las ecuaciones entre cantidades de magnitudes físicas sean dimensionalmente homogéneas (Principio de homogeneidad dimensional), es decir, exige que el signo igual sólo iguale términos que tengan las mismas dimensiones. El análisis dimensional, permite verificar la homogeneidad de los términos de una ecuación entre magnitudes físicas y, por lo tanto, si la ecuación es o no correcta. Por ejemplo, la ecuación: p=hpg Relaciona cantidades de presión hidrostática p, altura h de una columna líquida, densidad del líquido y la aceleración de gravedad g. Dimensionalmente es homogénea, como lo demuestra el siguiente análisis dimensional:
Finalmente, un sistema dimensional permite construir un sistema coherente de unidades de medida sobre la base de las unidades de las magnitudes básicas previamente fijadas y definidas.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” UNIDADES FUNDAMENTALES DEL “S. I.” El Sistema Internacional de Unidades (nombre abreviado: SI) adoptado en el año 1960 por la 11ª Conferencia General de Pesas y Medidas (CGPM), es una sistematización de las magnitudes físicas y sus unidades de medida sobre la base de siete magnitudes y unidades básicas o fundamentales. Dichas magnitudes son: la longitud, la masa, el tiempo, la corriente eléctrica, la temperatura termodinámica, la cantidad de substancia y la intensidad luminosa; y sus unidades de medida: el metro, el kilogramo, el segundo, el ampere, el kelvin, el mol y la candela, respectivamente. El precisar, sistematizar y normalizar la terminología metrológica, permite una comunicación científica más expedita, razón por la cual, en la actualidad, prácticamente todos los países se hallan adscritos a este sistema de unidades. Unidades básicas o fundamentales son las unidades elegidas como tales para las magnitudes básicas de un sistema. Unidades derivadas coherentes de un sistema son las unidades de las magnitudes derivadas, expresadas en términos de las unidades básicas del sistema. El conjunto de unidades básicas y derivadas coherentes, constituye un Sistema Coherente de Unidades de Medida. Un sistema de unidades es coherente, cuando todas las unidades derivadas del sistema se obtienen a partir de las unidades básicas por medio de operaciones algebraicas en las cuales todos los factores numéricos involucrados son iguales a 1. El Sistema Internacional de Unidades o Unidades SI, es un sistema coherente. También lo son los sistemas cgs, mks y fps o británico, dados en la Tabla 1.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
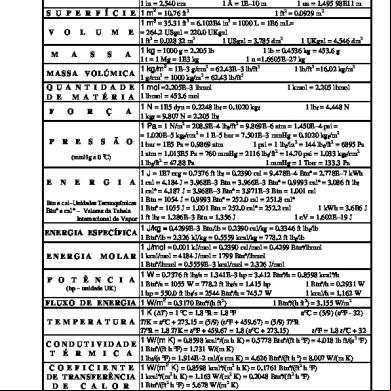
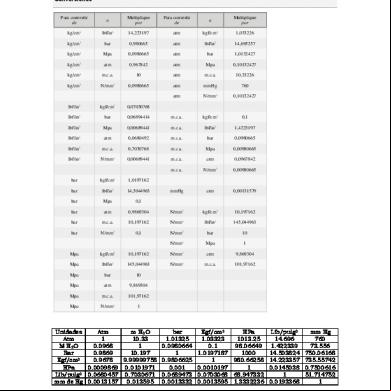
Un sistema coherente de unidades de medida se construye, definiendo primero las unidades básicas sobre la base de hechos físicos reales. Luego se definen las unidades derivadas coherentes en términos de las básicas. La Tabla 1 muestra las unidades básicas que han sido elegidas en los sistemas cgs, mks, británico e Internacional. La Tabla 2 contiene las definiciones adoptadas para las unidades básicas del Sistema Internacional.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
UNIDADES SUPLEMENTARIAS DEL “S. I.” El Sistema Internacional de Unidades, además de las magnitudes básicas y derivadas, considera una tercera clase de magnitudes físicas: las magnitudes suplementarias. Son el ángulo plano y el ángulo sólido magnitudes de naturaleza puramente geométricas. Las unidades SI, adoptadas para estas magnitudes, consideradas como unidades suplementarias, son el radián (símbolo, rad) y el estereoradián (símbolo, sr). Tabla 1. Magnitudes y Unidades SI suplementarias Magnitud
Unidad
Símbolo
Angulo plano
radián
rad
Angulo sólido
estereorradián sr
Este calificativo dejó abierta la posibilidad para que dichas magnitudes y unidades fueran consideradas y utilizadas como básicas o como derivadas. En química y en física las unidades, usualmente, son tratadas como unidades derivadas adimensionales, tratamiento reconocido por el Comité Internacional de Pesas y Medidas (CIPM) en Octubre de 1980. Sin embargo, durante la XX CGPM (1995) se decidió interpretar las unidades suplementarias radián y estereorradián como unidades derivadas adimensionales y, consecuentemente, eliminar la clase de unidades suplementarias como una clase separada del SI. DEFINICIÓN DEL RADIÁN Y ESTEREORRADIÁN Radián: es el ángulo plano entre dos radios de un círculo que cortan sobre la circunferencia un arco de longitud igual al radio (ISO 31/1-1992). Estereorradián: Es el ángulo sólido que, teniendo su vértice en el centro de una esfera, determina un área en la superficie de está igual a la de un cuadrado de lados iguales al radio de la esfera (ISO 31/1-1992).
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
BIBLIOGRAFIA
http://www.quimicabasica.cl/temas.htm http://es.wikipedia.org/wiki/Dimensi%C3%B3n http://www.google.com.mx/search? hl=es&biw=1362&bih=591&defl=es&q=define:Dimensi %C3%B3n&sa=X&ei=bC9BTaaKM5LAsAPRkPi8Cg&ved=0CBEQkAE
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” LA DIMENSION FISICA DE UNA MAGNITUD Las magnitudes físicas pueden ser expresadas en términos de las magnitudes básicas de un sistema por medio de expresiones conocidas como dimensiones físicas, cuya importancia, en el marco de un enfoque riguroso de la ciencia, es de inapreciable valor. En este contexto, ha sido posible organizar sistemas dimensionales construidos sobre la base de un grupo de magnitudes, elegidas como magnitudes básicas o fundamentales, cuyas dimensiones serían las dimensiones básicas del sistema. En el Sistema Mecánico las dimensiones de las magnitudes básicas (dimensiones básicas), se representan por medio de las letras L, M y T para la longitud, la masa y el tiempo, respectivamente. En el Sistema Internacional, a las anteriores, se agregan las letras I, O, N y J para la corriente eléctrica, la temperatura termodinámica, la cantidad de substancia y la intensidad luminosa, respectivamente. Las dimensiones de una magnitud física Q cualquiera, en un sistema dado, quedará expresada por medio de un producto de potencias de las dimensiones básicas del sistema considerado Así, en los sistemas mecánico e internacional se tiene:
En donde los exponentes son los exponentes dimensionales cuyos valores, característicos para cada magnitud física, pueden ser mayores, iguales o menores que cero. Por ejemplo, para la energía molar se tiene:
En donde xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx considerando, que toda potencia de exponente cero es igual a 1.
y
Si todos los exponentes dimensionales de la magnitud Q fueran iguales a cero, su producto dimensional sería igual a 1:
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” En este caso, la magnitud física Q es adimensional. Ejemplos, la densidad relativa, la fracción molar, etc. La dimensión de una magnitud básica se tiene cuando el exponente dimensional de su dimensión básica es igual a 1, e igual a cero los exponentes de las otras dimensiones básicas. Por ejemplo:
Las dimensiones de las magnitudes derivadas se obtienen a partir de las ecuaciones matemáticas que las definen o de las que expresan leyes físicas. Por ejemplo:
Bibliografia: http://es.wikipedia.org/wiki/Dimensi%C3%B3n http://www.quimicabasica.cl/temas.htm
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” Puede apreciarse, que la dimensión física de una magnitud, en un sistema dado, nos informa sobre el cómo se halla relacionada o se deriva de las magnitudes básicas del sistema. Por ejemplo, la velocidad se deriva de la longitud y el tiempo, pues sus dimensiones LT-1 nos indica que es una longitud dividida por un tiempo. La fuerza se deriva de la longitud, la masa y el tiempo, pues sus dimensiones MLT-2 nos indica que es una masa por una longitud dividida por un tiempo al cuadrado. El empleo de un sistema dimensional nos permite, por una parte, identificar a las magnitudes físicas, considerando el hecho de que tienen diferentes dimensiones físicas. Por otra parte, exige que las ecuaciones entre cantidades de magnitudes físicas sean dimensionalmente homogéneas (Principio de homogeneidad dimensional), es decir, exige que el signo igual sólo iguale términos que tengan las mismas dimensiones. El análisis dimensional, permite verificar la homogeneidad de los términos de una ecuación entre magnitudes físicas y, por lo tanto, si la ecuación es o no correcta. Por ejemplo, la ecuación: p=hpg Relaciona cantidades de presión hidrostática p, altura h de una columna líquida, densidad del líquido y la aceleración de gravedad g. Dimensionalmente es homogénea, como lo demuestra el siguiente análisis dimensional:
Finalmente, un sistema dimensional permite construir un sistema coherente de unidades de medida sobre la base de las unidades de las magnitudes básicas previamente fijadas y definidas.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.” UNIDADES FUNDAMENTALES DEL “S. I.” El Sistema Internacional de Unidades (nombre abreviado: SI) adoptado en el año 1960 por la 11ª Conferencia General de Pesas y Medidas (CGPM), es una sistematización de las magnitudes físicas y sus unidades de medida sobre la base de siete magnitudes y unidades básicas o fundamentales. Dichas magnitudes son: la longitud, la masa, el tiempo, la corriente eléctrica, la temperatura termodinámica, la cantidad de substancia y la intensidad luminosa; y sus unidades de medida: el metro, el kilogramo, el segundo, el ampere, el kelvin, el mol y la candela, respectivamente. El precisar, sistematizar y normalizar la terminología metrológica, permite una comunicación científica más expedita, razón por la cual, en la actualidad, prácticamente todos los países se hallan adscritos a este sistema de unidades. Unidades básicas o fundamentales son las unidades elegidas como tales para las magnitudes básicas de un sistema. Unidades derivadas coherentes de un sistema son las unidades de las magnitudes derivadas, expresadas en términos de las unidades básicas del sistema. El conjunto de unidades básicas y derivadas coherentes, constituye un Sistema Coherente de Unidades de Medida. Un sistema de unidades es coherente, cuando todas las unidades derivadas del sistema se obtienen a partir de las unidades básicas por medio de operaciones algebraicas en las cuales todos los factores numéricos involucrados son iguales a 1. El Sistema Internacional de Unidades o Unidades SI, es un sistema coherente. También lo son los sistemas cgs, mks y fps o británico, dados en la Tabla 1.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
Un sistema coherente de unidades de medida se construye, definiendo primero las unidades básicas sobre la base de hechos físicos reales. Luego se definen las unidades derivadas coherentes en términos de las básicas. La Tabla 1 muestra las unidades básicas que han sido elegidas en los sistemas cgs, mks, británico e Internacional. La Tabla 2 contiene las definiciones adoptadas para las unidades básicas del Sistema Internacional.
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
UNIDADES SUPLEMENTARIAS DEL “S. I.” El Sistema Internacional de Unidades, además de las magnitudes básicas y derivadas, considera una tercera clase de magnitudes físicas: las magnitudes suplementarias. Son el ángulo plano y el ángulo sólido magnitudes de naturaleza puramente geométricas. Las unidades SI, adoptadas para estas magnitudes, consideradas como unidades suplementarias, son el radián (símbolo, rad) y el estereoradián (símbolo, sr). Tabla 1. Magnitudes y Unidades SI suplementarias Magnitud
Unidad
Símbolo
Angulo plano
radián
rad
Angulo sólido
estereorradián sr
Este calificativo dejó abierta la posibilidad para que dichas magnitudes y unidades fueran consideradas y utilizadas como básicas o como derivadas. En química y en física las unidades, usualmente, son tratadas como unidades derivadas adimensionales, tratamiento reconocido por el Comité Internacional de Pesas y Medidas (CIPM) en Octubre de 1980. Sin embargo, durante la XX CGPM (1995) se decidió interpretar las unidades suplementarias radián y estereorradián como unidades derivadas adimensionales y, consecuentemente, eliminar la clase de unidades suplementarias como una clase separada del SI. DEFINICIÓN DEL RADIÁN Y ESTEREORRADIÁN Radián: es el ángulo plano entre dos radios de un círculo que cortan sobre la circunferencia un arco de longitud igual al radio (ISO 31/1-1992). Estereorradián: Es el ángulo sólido que, teniendo su vértice en el centro de una esfera, determina un área en la superficie de está igual a la de un cuadrado de lados iguales al radio de la esfera (ISO 31/1-1992).
UNIDAD 2 CONCEPTOS BASICOS DE METROLOGIA 2.5 DIMENSIONES, UNIDADES FUNDAMENTALES Y SUPLEMENTARIAS DEL “S.I.”
BIBLIOGRAFIA
http://www.quimicabasica.cl/temas.htm http://es.wikipedia.org/wiki/Dimensi%C3%B3n http://www.google.com.mx/search? hl=es&biw=1362&bih=591&defl=es&q=define:Dimensi %C3%B3n&sa=X&ei=bC9BTaaKM5LAsAPRkPi8Cg&ved=0CBEQkAE