Diferencia Entre Pendiente De Una Recta Tangente Y Secante. 221r3f
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Diferencia Entre Pendiente De Una Recta Tangente Y Secante. as PDF for free.
More details 6z3438
- Words: 406
- Pages: 3
Diferencia ente Pendiente de una recta tangente y secante. La pendiente de la recta secante tiende a ser la pendiente de la recta tangente en una proximidad muy cercana del punto .- Esa es la relación , su proximidad al punto .Matemáticamente esto es que si existen dos puntos cercanos (x,f(x)) y ((x+h), f(x+h)) , la pendiente será m=
(
f (x +h)−f ( x ) ) h
y corresponde a una
secante .- En la medida que exista proximidad en los dos puntos , h---->0 y pasa a ser tangente .- Por eso es muy diferente hablar de diferencia infenitesimal dx que diferencial Dx .- La diferencial Dx, la usa la secante , la infinitesimal dx, la usa la tangente .También existe otra interpretación que es muy importante. La recta tangente a una curva en un punto es una recta que sólo toca a la función en ese punto.
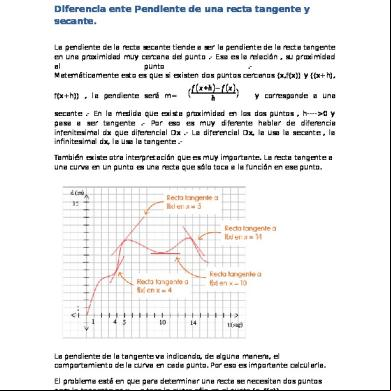
La pendiente de la tangente va indicando, de alguna manera, el comportamiento de la curva en cada punto. Por eso es importante calcularla. El problema está en que para determinar una recta se necesitan dos puntos pero la tangente en x = a toca la curva sólo en el punto (a, f(a)).
La que es fácil determinar es una recta secante, es decir que corte a la curva en dos puntos. Uno correspondiente a x = a y otro a una distancia h de éste, es decir, x = a + h. Esta recta se aproxima a la tangente en a.
Pero esa distancia h ¿cuánto vale? En realidad basta con pensar que es un valor pequeño, porque cuanto menor sea, más se aparecerá la secante a la tangente.
Es decir, tienen un punto en común y las pendientes se van pareciendo cada vez más.
Observemos que la pendiente de la secante es delta y sobre delta x, es decir la variación de la función sobre la variación de la variable independiente. Pendiente de la secante que pasa por a
Es el cociente incremental. El límite de este cociente, cuando h tiende a cero, será entonces, la pendiente de la recta tangente a la curva en ese punto.
Entonces, la derivada de una función se puede interpretar como la pendiente de la recta tangente en ese punto. Derivada de f(x) en a
Entonces, de alguna manera, la pendiente de la recta tangente en un punto y la razón instantánea de cambio, en ese punto, están vinculadas.
(
f (x +h)−f ( x ) ) h
y corresponde a una
secante .- En la medida que exista proximidad en los dos puntos , h---->0 y pasa a ser tangente .- Por eso es muy diferente hablar de diferencia infenitesimal dx que diferencial Dx .- La diferencial Dx, la usa la secante , la infinitesimal dx, la usa la tangente .También existe otra interpretación que es muy importante. La recta tangente a una curva en un punto es una recta que sólo toca a la función en ese punto.
La pendiente de la tangente va indicando, de alguna manera, el comportamiento de la curva en cada punto. Por eso es importante calcularla. El problema está en que para determinar una recta se necesitan dos puntos pero la tangente en x = a toca la curva sólo en el punto (a, f(a)).
La que es fácil determinar es una recta secante, es decir que corte a la curva en dos puntos. Uno correspondiente a x = a y otro a una distancia h de éste, es decir, x = a + h. Esta recta se aproxima a la tangente en a.
Pero esa distancia h ¿cuánto vale? En realidad basta con pensar que es un valor pequeño, porque cuanto menor sea, más se aparecerá la secante a la tangente.
Es decir, tienen un punto en común y las pendientes se van pareciendo cada vez más.
Observemos que la pendiente de la secante es delta y sobre delta x, es decir la variación de la función sobre la variación de la variable independiente. Pendiente de la secante que pasa por a
Es el cociente incremental. El límite de este cociente, cuando h tiende a cero, será entonces, la pendiente de la recta tangente a la curva en ese punto.
Entonces, la derivada de una función se puede interpretar como la pendiente de la recta tangente en ese punto. Derivada de f(x) en a
Entonces, de alguna manera, la pendiente de la recta tangente en un punto y la razón instantánea de cambio, en ese punto, están vinculadas.