Sistem Arus Bolak Balik 3 Fasa.pdf 4c3x1m
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Sistem Arus Bolak Balik 3 Fasa.pdf as PDF for free.
More details 6z3438
- Words: 2,301
- Pages: 13
RANGKAIAN LISTRIK TIGA FASA
OLEH:
IFKAR USRAH
JURUSAN TEKNIK ELEKTRO FAKULTAS TEKNIK UNIVERSITAS SILIWANGI TASIKMALAYA
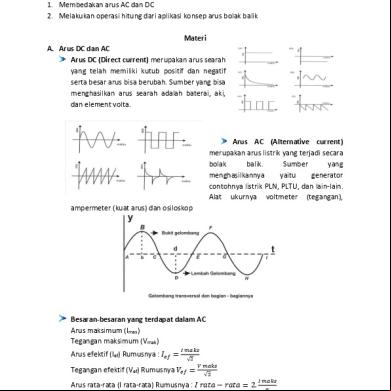
SISTEM TIGA FASA Kebanyakan sistem listrik dibangun dengan sistem tiga fasa. Hal tersebut didasarkan pada alasan-alasan ekonomi dan kestabilan aliran daya pada beban. Alasan ekonomi dikarenakan dengan sistem tiga fasa, penggunaan penghantar untuk transmisi menjadi lebih sedikit. Sedangkan alasan kestabilan dikarenakan pada sistem tiga fasa daya mengalir sebagai layaknya tiga buah sistem fasa tunggal, sehingga untuk peralatan dengan catu tiga fasa, daya sistem akan lebih stabil bila dibandingkan dengan peralatan dengan sistem satu fasa. Sistem tiga fasa atau sistem fasa banyak lainnya, secara umum akan memunculkan sistem yang lebih kompleks, akan tetapi secara prinsip untuk analisa, sistem tetap mudah dilaksanakan. Sistem tiga fasa dapat digambarkan dengan suatu sistem yang terdiri dari tiga sistem fasa tunggal, sebagai berikut : + + Vc
+ Vb Vc j
2 3
-
Vb j23
-
Va Va
-
-
-
Gambar 1 Sistem Tiga Fasa Sebagai Tiga Sistem Fasa Tunggal. Va = Vm sin t Vb = Vm sin (t - 1200) Vc = Vm sin (t + 1200) Sedangkan bentuk gelombang dari sistem tiga fasa yang merupakan fungsi waktu ditunjukkan pada gambar berikut.
Va
1
Vc
Vb
ggl
0.5 0 - 0.5 -1 90
0
180
220
380
t
Gambar 2 Bentuk Gelombang Pada Sistem Tiga Fasa Pada gambar nampak bahwa antara tegangan fasa satu dengan yang lainnya mempunyai perbedaan fase sebesar 120o atau 2/3. Pada umumnya fasa dengan sudut fasa 0o disebut dengan fasa R, fasa dengan sudut fasa 120o disebut fasa S dan fasa dengan sudut fasa 240o disebut dengan fasa T. Perbedaaan sudut fasa tersebut pada pembangkit dimulai dari adanya kumparan yang masing-masing tersebar secara terpisah dengan jarak 120o.
Sistem Y dan Sistem Y merupakan sistem sambungan pada sistem tiga fasa yang menggunakan empat Line, yaitu fasa R, S, T dan N. Sistem sambungan tersebut akan menyerupai huruf Y, yang memiliki empat titik sambungan yaitu pada ujung-ujung huruf dan pada titik pertemuan antara tiga garis pembentuk huruf. Sistem Y dapat digambarkan dengan skema berikut. R
S Z
R
Z N
Z
Z
Z T T
(A)
Z
S
(B)
Gambar 3 (A) Sistem Y (wye) dan (B) Sistem Delta
Sistem hubungan atau sambungan Y, sering juga disebut sebagai hubungan bintang. Sedangkan pada sistem yang lain yang disebut sebagai sistem Delta, hanya menggunakan fasa R, S dan T untuk hubungan dari sumber ke beban, sebagaimana gambar diatas.Tegangan efektif antar fasa umumnya adalah 380 V dan tegangan efektif fasa ke netral adalah 220 V.
Beban Seimbang Terhubung Y Analisis rangkaian tiga fasa beban seimbang hubungan bintang 4 Line sama dengan beban tidak seimbang karena ketiga impedansi beban sama maka besarnya arus sama di semua Line yang berbeda hanya sudutnya saja masing-masing berbeda 1200 Ia
A
a
ZA Z
Van In
n Vcn
Vbn
N
ZC Z
ZB Z
Ic c
C
B
Ib b
Gambar 4 Beban seimbang terhubung Y (Wye) V V 0 Ia an an IL IL A ZA Z
V V 1200 Ib bn bn IL 1200 IL 1200 A ZB Z V V 1200 Ic an an IL1200 IL1200 A ZA Z
Menghitung arus yang mengalir pada Line netral kita gunakan KCL (Kirhoff Current Low) pada titik netral adalah In -Ia -Ib -Ic 0 sehingga In = - Ia +Ib +I I 0
Daya pada beban hubungan bintang empat Line
Daya nyata Daya nyata pada fasa A : PA = Van Ia cos A VLNIL cos Vf If cos (w) Daya nyata pada fasa B : Pb = Vbn Ib cos B VLNIL cos Vf If cos (w) Daya nyata pada fasa C : PC = Vcn Ic cos C VLNIL cos Vf If cos (w) Daya nyata tiga fasa : P3fasa = PA PB PC 3.Vf If cos watt Daya reaktif : Daya reaktif pada fasa A : QA = Van Ia sin A VLNIL sin Vf If sin (VAR) Daya reaktif pada fasa B : Qb = Vbn Ib sin B VLNIL sin Vf If sin (VAR) Daya reaktif pada fasa C : QC = Vcn Ic sin C VLNIL sin Vf If sin (VAR) Daya reaktif tiga fasa : Q3fasa = QA QB QC Berdasarkan besaran fasa : Q3fasa = 3.Vf If sin var
Berdasarkan besar line atau Line : Q3fasa = 3.VLLIL sin var
Daya semu : Daya semu pada fasa A : SA = Van Ia VLNIL Vf If volt ampere (VA) Daya semu pada fasa B : SB = Vbn Ib VLNIL Vf If volt ampere (VA) Daya semu pada fasa C : SC = Vcn Ic VLNIL Vf If volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC Berdasarkan besaran fasa : S3fasa = 3.Vf If VA
Berdasarkan besaran line atau Line : S3fasa = 3.VLLIL var
VC IC φ
VA φ φ IA
IB
VB
Gambar 5 Diagram vector arus beban seimbang hubungan Y (Wye) Beban Tak Seimbang Terhubung Y Pada sistem ini masing-masing fase akan mengalirkan arus yang tak seimbang menuju Netral (pada sistem empat Line). Sedangkan pada sistem tiga Line akan mengakibatkan tegangan yang berubah cukup signifikan dan memunculkan suatu netral yang berbeda dari netral yang semestinya.
Ia
Ia
Z1 ZA
Van In
n Vcn
A I1
a
A
a
Vbn
Vab
N ZC
c
ZC
Ic C
B
c
C
ZB B
Vbc
Ib b
N
Vab
ZB
Ic
Z1 ZA
I2
Ib b
(A)
(B)
Gambar 6. (A) Beban tak seimbang terhubung bintang empat Line dan (B) Beban tak seimbang terhubung bintang tiga Line
VC
IC
VA IB
IA
VB
Gambar 6. Diagram vector arus beban Tak seimbang hubungan Y (Wye) Arus pada beban hubungan bintang empat Line Dengan metode arus lup diperoleh persamaan arus sebagi berikut ( lihat gambar.....) Ia
VAN VLN V V V V , Ib BN LN , Ic CN LN Za ZA Zb ZA Zc ZC
Arus yang mengalir pada Line netral kita gunakan KCL (Kirhoff Current Low) pada titik N, diperoleh. In +Ia +Ib +Ic 0 sehingga In = - Ia +Ib +Ic
Daya pada beban hubungan bintang empat Line Daya nyata Daya nyata pada fasa A : PA = Van Ia cos A (w) Daya nyata pada fasa B : Pb = Vbn Ib cos B (w) Daya nyata pada fasa C : PC = Vcn Ic cos C (w) Daya Aktif tiga fasa:
P3 = PA + PB + PC
Daya reaktif : Daya reaktif pada fasa A : QA = Van Ia sin A (VAR) Daya reaktif pada fasa B : Qb = Vbn Ib sin B (VAR) Daya reaktif pada fasa C : QC = Vcn Ic sin C (VAR) Daya reaktif tiga fasa
: Q3fasa = QA QB QC
Daya semu : Daya semu pada fasa A : SA = Van Ia volt ampere (VA) Daya semu pada fasa B : Sb = Vbn Ib volt ampere (VA) Daya semu pada fasa C : Sc = Vcn Ic volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC
Sedangkan pada sistem tiga Line ini titik netral beban tidak dihubungkan dengan titik netral sumber sehingga tegangan yang digunakan adalah tegangan line to line (V LL) dari sumber. Untuk menghitung arus pada setiap Line digunakan metode arus lup, sebagai berikut: Dapat digunakan dua arus lup atau tiga arus lup, misal digunakan dua buah arus lup, yaitu : 1. arus lup yang melewati a-A-N-B-b-a=I1 2. arus lup yang melewati c-C-N-A-a-c=I2 diperoleh dua persamaan 1 dan persamaan 2 diperoleh I1 dan I2, sehingga arus Line dapat dihitung dari arus lup, ( lihat gambar 3.8 ) Ia=I1-I2 ; Ib = - I1 dan Ic=I2 dimana Ia + Ib + Ic = 0
Daya pada beban hubungan bintang tiga Line :
Daya nyata Daya nyata pada fasa A : PA = VANIa cos A (w) Daya nyata pada fasa B : PB = VBNIb cos B (w) Daya nyata pada fasa C : PC = VCNIc cos C (w) Daya nyata tiga fasa : P3fasa = PA PB PC Daya reaktif : Daya reaktif pada fasa A : QA = VAN Ia sin A (VAR) Daya reaktif pada fasa B : QB = VBNIb sin B (VAR) Daya reaktif pada fasa C : QC = VCNIc sin C (VAR) Daya reaktif tiga fasa : Q3fasa = QA QB QC Daya semu : Daya semu pada fasa A : SA = VANIa volt ampere (VA) Daya semu pada fasa B : SB = VBNIb volt ampere (VA) Daya semu pada fasa C : SC = VCNIc volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC
Beban Seimbang Terhubung Delta Pada sitem delta, bila tiga buah beban dengan impedansi yang sama disambungkan pada sumber tiga fasa, maka arus di dalam ketiga impedansai akan sama besar tetapi terpisah dengan sudut sebesar 120o, dan dikenal dengan arus fasa atau arus beban. Untuk keadaan yang demikian, maka dalam rangkaian akan berlaku :
A
A Ia VAB VCA
ICA
ZAB = Z<
IAB
ZCA = Z<
IBC IB B
B
C ZBC = Z<
VBC Ic C
Gambar 7. Beban seimbang terhubung Delta Arus fasa : VAB Vab VLL00 VLL If A ZAB ZAB Z Z 0 V V V V - IBC = BC bc LL120 LL 1200 If 1200 A ZBC ZBC Z Z VCA Vca VLL1200 VLL - ICA = 1200 If 1200 A ZCA ZCA Z Z - IAB =
Arus Line : - Ia = IAB ICA If If 1200 3.If 300 A - Ib = IBC IAB If 1200 If 3.If 1200 300 A - Ic = ICA IBC If 1200 If 1200 3.If 1200 300 A
Daya pada beban : Daya semu: S3fasa SAB SBC SCA VAB IAB VBC IBC VCA ICA Daya nyata :
P3fasa PAB PBC PCA
Dimana : PAB VABIAB cos AB Vf If cos watt PBC VBCIBC cos BC Vf If cos watt PCA VCAICA cos CA Vf If cos watt
Jadi P3fasa PAB PBC PCA 3.Vf If cos watt Daya reaktif
Q3fasa QAB QBC QCA
Dimana : QAB VABIAB sin AB Vf If sin watt PBC VBCIBC sin BC Vf If sin watt PCA VCAICA sin CA Vf If sin watt
Daya semu: S3fasa SAB SBC SCA VAB IAB VBC IBC VCA ICA
S3fasa 3.Vf If VA
Karena pada beban seimbang ada hubungan Vf =VLL dan VL = IL maka rumus daya dapat 3
dituliskan sebagai berikut : Berdasarkan harga perfasa : P3fasa 3.Vf If cos watt ; Q3fasa 3.Vf If sin var dan S3fasa 3.Vf If VA
Berdasarkan harga antar Line (antara line) P3fasa 3.VLLIL cos watt ; Q3fasa 3.VLLIL sin var dan S3fasa 3.Vf If VA ..139
Ic VCA ICA - IAB - IBC
Ib
VAB
IAB
IBC
- ICA VBC Ia
Gambar 8. Diagram vector arus beban seimbang hubungan delta
Beban Tak Seimbang Terhubung Delta Beban tak seimbang yang direfresentasikan dengan tiga buah impedansi masing-masing Z1 . Z2 . Z3 yang dihubungkan delta yang dapat dicatu sumber hubungan delta maupun sumber hubungan bintang. Pada system tiga fasa hubungan delta terdapat dua macam arus, yaitu arus Line (IL) dan arus fasa (If). Arus Line yaitu arus yang mengalir pada Line penghantar terdiri dari Ia ; IB dan IC. Arus fasa yaitu arus yang mengalir didalam impedansi setiap fasa terdiri dari IAB; IBC dan IAB
A
a Ia
ICA
VCA
ZAC
VAB Ic C
c
ZAB IBC
IAB
B
ZBC VBC Ib b
Gambar 9. Beban tak seimbang terhubung Delta Untuk menghitung arus dan daya pada rangkaian 3 fasa hubungan delta digunakan metode arus lup yang akhirnya menghasilkan : Arus fasa :
IAB
VAB Vab ZAB ZAB
IBC
VBC Vbc ZBC ZBC
ICA
VCA Vca ZCA ZCA
Arus Line :
Ia IAB ICA
Ib IBC IAB
Ic ICA IBC
Daya pada Beban : Daya semu
: S3fasa = SAB + SBC + SCA = VAB(IAB)0 +VBC(IBC)0 + VCA(ICA)0
Daya nyata
: P3fasa= PAB + PBC + PCA
Dimana PAB= VABIAB cos AB PBC= VBCIBC cos BC PCA= VCAICA cos CA Daya Reaktif : Q3fasa= QAB + QBC + QCA Dimana QAB= VABIAB sin AB QBC= VBCIBC sin BC QCA= VCAICA sin CA
VCA
IC IB VAB
IA VBC
Gambar 10 Diagram vector arus beban Tak seimbang hubungan delta
OLEH:
IFKAR USRAH
JURUSAN TEKNIK ELEKTRO FAKULTAS TEKNIK UNIVERSITAS SILIWANGI TASIKMALAYA
SISTEM TIGA FASA Kebanyakan sistem listrik dibangun dengan sistem tiga fasa. Hal tersebut didasarkan pada alasan-alasan ekonomi dan kestabilan aliran daya pada beban. Alasan ekonomi dikarenakan dengan sistem tiga fasa, penggunaan penghantar untuk transmisi menjadi lebih sedikit. Sedangkan alasan kestabilan dikarenakan pada sistem tiga fasa daya mengalir sebagai layaknya tiga buah sistem fasa tunggal, sehingga untuk peralatan dengan catu tiga fasa, daya sistem akan lebih stabil bila dibandingkan dengan peralatan dengan sistem satu fasa. Sistem tiga fasa atau sistem fasa banyak lainnya, secara umum akan memunculkan sistem yang lebih kompleks, akan tetapi secara prinsip untuk analisa, sistem tetap mudah dilaksanakan. Sistem tiga fasa dapat digambarkan dengan suatu sistem yang terdiri dari tiga sistem fasa tunggal, sebagai berikut : + + Vc
+ Vb Vc j
2 3
-
Vb j23
-
Va Va
-
-
-
Gambar 1 Sistem Tiga Fasa Sebagai Tiga Sistem Fasa Tunggal. Va = Vm sin t Vb = Vm sin (t - 1200) Vc = Vm sin (t + 1200) Sedangkan bentuk gelombang dari sistem tiga fasa yang merupakan fungsi waktu ditunjukkan pada gambar berikut.
Va
1
Vc
Vb
ggl
0.5 0 - 0.5 -1 90
0
180
220
380
t
Gambar 2 Bentuk Gelombang Pada Sistem Tiga Fasa Pada gambar nampak bahwa antara tegangan fasa satu dengan yang lainnya mempunyai perbedaan fase sebesar 120o atau 2/3. Pada umumnya fasa dengan sudut fasa 0o disebut dengan fasa R, fasa dengan sudut fasa 120o disebut fasa S dan fasa dengan sudut fasa 240o disebut dengan fasa T. Perbedaaan sudut fasa tersebut pada pembangkit dimulai dari adanya kumparan yang masing-masing tersebar secara terpisah dengan jarak 120o.
Sistem Y dan Sistem Y merupakan sistem sambungan pada sistem tiga fasa yang menggunakan empat Line, yaitu fasa R, S, T dan N. Sistem sambungan tersebut akan menyerupai huruf Y, yang memiliki empat titik sambungan yaitu pada ujung-ujung huruf dan pada titik pertemuan antara tiga garis pembentuk huruf. Sistem Y dapat digambarkan dengan skema berikut. R
S Z
R
Z N
Z
Z
Z T T
(A)
Z
S
(B)
Gambar 3 (A) Sistem Y (wye) dan (B) Sistem Delta
Sistem hubungan atau sambungan Y, sering juga disebut sebagai hubungan bintang. Sedangkan pada sistem yang lain yang disebut sebagai sistem Delta, hanya menggunakan fasa R, S dan T untuk hubungan dari sumber ke beban, sebagaimana gambar diatas.Tegangan efektif antar fasa umumnya adalah 380 V dan tegangan efektif fasa ke netral adalah 220 V.
Beban Seimbang Terhubung Y Analisis rangkaian tiga fasa beban seimbang hubungan bintang 4 Line sama dengan beban tidak seimbang karena ketiga impedansi beban sama maka besarnya arus sama di semua Line yang berbeda hanya sudutnya saja masing-masing berbeda 1200 Ia
A
a
ZA Z
Van In
n Vcn
Vbn
N
ZC Z
ZB Z
Ic c
C
B
Ib b
Gambar 4 Beban seimbang terhubung Y (Wye) V V 0 Ia an an IL IL A ZA Z
V V 1200 Ib bn bn IL 1200 IL 1200 A ZB Z V V 1200 Ic an an IL1200 IL1200 A ZA Z
Menghitung arus yang mengalir pada Line netral kita gunakan KCL (Kirhoff Current Low) pada titik netral adalah In -Ia -Ib -Ic 0 sehingga In = - Ia +Ib +I I 0
Daya pada beban hubungan bintang empat Line
Daya nyata Daya nyata pada fasa A : PA = Van Ia cos A VLNIL cos Vf If cos (w) Daya nyata pada fasa B : Pb = Vbn Ib cos B VLNIL cos Vf If cos (w) Daya nyata pada fasa C : PC = Vcn Ic cos C VLNIL cos Vf If cos (w) Daya nyata tiga fasa : P3fasa = PA PB PC 3.Vf If cos watt Daya reaktif : Daya reaktif pada fasa A : QA = Van Ia sin A VLNIL sin Vf If sin (VAR) Daya reaktif pada fasa B : Qb = Vbn Ib sin B VLNIL sin Vf If sin (VAR) Daya reaktif pada fasa C : QC = Vcn Ic sin C VLNIL sin Vf If sin (VAR) Daya reaktif tiga fasa : Q3fasa = QA QB QC Berdasarkan besaran fasa : Q3fasa = 3.Vf If sin var
Berdasarkan besar line atau Line : Q3fasa = 3.VLLIL sin var
Daya semu : Daya semu pada fasa A : SA = Van Ia VLNIL Vf If volt ampere (VA) Daya semu pada fasa B : SB = Vbn Ib VLNIL Vf If volt ampere (VA) Daya semu pada fasa C : SC = Vcn Ic VLNIL Vf If volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC Berdasarkan besaran fasa : S3fasa = 3.Vf If VA
Berdasarkan besaran line atau Line : S3fasa = 3.VLLIL var
VC IC φ
VA φ φ IA
IB
VB
Gambar 5 Diagram vector arus beban seimbang hubungan Y (Wye) Beban Tak Seimbang Terhubung Y Pada sistem ini masing-masing fase akan mengalirkan arus yang tak seimbang menuju Netral (pada sistem empat Line). Sedangkan pada sistem tiga Line akan mengakibatkan tegangan yang berubah cukup signifikan dan memunculkan suatu netral yang berbeda dari netral yang semestinya.
Ia
Ia
Z1 ZA
Van In
n Vcn
A I1
a
A
a
Vbn
Vab
N ZC
c
ZC
Ic C
B
c
C
ZB B
Vbc
Ib b
N
Vab
ZB
Ic
Z1 ZA
I2
Ib b
(A)
(B)
Gambar 6. (A) Beban tak seimbang terhubung bintang empat Line dan (B) Beban tak seimbang terhubung bintang tiga Line
VC
IC
VA IB
IA
VB
Gambar 6. Diagram vector arus beban Tak seimbang hubungan Y (Wye) Arus pada beban hubungan bintang empat Line Dengan metode arus lup diperoleh persamaan arus sebagi berikut ( lihat gambar.....) Ia
VAN VLN V V V V , Ib BN LN , Ic CN LN Za ZA Zb ZA Zc ZC
Arus yang mengalir pada Line netral kita gunakan KCL (Kirhoff Current Low) pada titik N, diperoleh. In +Ia +Ib +Ic 0 sehingga In = - Ia +Ib +Ic
Daya pada beban hubungan bintang empat Line Daya nyata Daya nyata pada fasa A : PA = Van Ia cos A (w) Daya nyata pada fasa B : Pb = Vbn Ib cos B (w) Daya nyata pada fasa C : PC = Vcn Ic cos C (w) Daya Aktif tiga fasa:
P3 = PA + PB + PC
Daya reaktif : Daya reaktif pada fasa A : QA = Van Ia sin A (VAR) Daya reaktif pada fasa B : Qb = Vbn Ib sin B (VAR) Daya reaktif pada fasa C : QC = Vcn Ic sin C (VAR) Daya reaktif tiga fasa
: Q3fasa = QA QB QC
Daya semu : Daya semu pada fasa A : SA = Van Ia volt ampere (VA) Daya semu pada fasa B : Sb = Vbn Ib volt ampere (VA) Daya semu pada fasa C : Sc = Vcn Ic volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC
Sedangkan pada sistem tiga Line ini titik netral beban tidak dihubungkan dengan titik netral sumber sehingga tegangan yang digunakan adalah tegangan line to line (V LL) dari sumber. Untuk menghitung arus pada setiap Line digunakan metode arus lup, sebagai berikut: Dapat digunakan dua arus lup atau tiga arus lup, misal digunakan dua buah arus lup, yaitu : 1. arus lup yang melewati a-A-N-B-b-a=I1 2. arus lup yang melewati c-C-N-A-a-c=I2 diperoleh dua persamaan 1 dan persamaan 2 diperoleh I1 dan I2, sehingga arus Line dapat dihitung dari arus lup, ( lihat gambar 3.8 ) Ia=I1-I2 ; Ib = - I1 dan Ic=I2 dimana Ia + Ib + Ic = 0
Daya pada beban hubungan bintang tiga Line :
Daya nyata Daya nyata pada fasa A : PA = VANIa cos A (w) Daya nyata pada fasa B : PB = VBNIb cos B (w) Daya nyata pada fasa C : PC = VCNIc cos C (w) Daya nyata tiga fasa : P3fasa = PA PB PC Daya reaktif : Daya reaktif pada fasa A : QA = VAN Ia sin A (VAR) Daya reaktif pada fasa B : QB = VBNIb sin B (VAR) Daya reaktif pada fasa C : QC = VCNIc sin C (VAR) Daya reaktif tiga fasa : Q3fasa = QA QB QC Daya semu : Daya semu pada fasa A : SA = VANIa volt ampere (VA) Daya semu pada fasa B : SB = VBNIb volt ampere (VA) Daya semu pada fasa C : SC = VCNIc volt ampere (VA) Daya semu tiga fasa : S3fasa = SA SB SC
Beban Seimbang Terhubung Delta Pada sitem delta, bila tiga buah beban dengan impedansi yang sama disambungkan pada sumber tiga fasa, maka arus di dalam ketiga impedansai akan sama besar tetapi terpisah dengan sudut sebesar 120o, dan dikenal dengan arus fasa atau arus beban. Untuk keadaan yang demikian, maka dalam rangkaian akan berlaku :
A
A Ia VAB VCA
ICA
ZAB = Z<
IAB
ZCA = Z<
IBC IB B
B
C ZBC = Z<
VBC Ic C
Gambar 7. Beban seimbang terhubung Delta Arus fasa : VAB Vab VLL00 VLL If A ZAB ZAB Z Z 0 V V V V - IBC = BC bc LL120 LL 1200 If 1200 A ZBC ZBC Z Z VCA Vca VLL1200 VLL - ICA = 1200 If 1200 A ZCA ZCA Z Z - IAB =
Arus Line : - Ia = IAB ICA If If 1200 3.If 300 A - Ib = IBC IAB If 1200 If 3.If 1200 300 A - Ic = ICA IBC If 1200 If 1200 3.If 1200 300 A
Daya pada beban : Daya semu: S3fasa SAB SBC SCA VAB IAB VBC IBC VCA ICA Daya nyata :
P3fasa PAB PBC PCA
Dimana : PAB VABIAB cos AB Vf If cos watt PBC VBCIBC cos BC Vf If cos watt PCA VCAICA cos CA Vf If cos watt
Jadi P3fasa PAB PBC PCA 3.Vf If cos watt Daya reaktif
Q3fasa QAB QBC QCA
Dimana : QAB VABIAB sin AB Vf If sin watt PBC VBCIBC sin BC Vf If sin watt PCA VCAICA sin CA Vf If sin watt
Daya semu: S3fasa SAB SBC SCA VAB IAB VBC IBC VCA ICA
S3fasa 3.Vf If VA
Karena pada beban seimbang ada hubungan Vf =VLL dan VL = IL maka rumus daya dapat 3
dituliskan sebagai berikut : Berdasarkan harga perfasa : P3fasa 3.Vf If cos watt ; Q3fasa 3.Vf If sin var dan S3fasa 3.Vf If VA
Berdasarkan harga antar Line (antara line) P3fasa 3.VLLIL cos watt ; Q3fasa 3.VLLIL sin var dan S3fasa 3.Vf If VA ..139
Ic VCA ICA - IAB - IBC
Ib
VAB
IAB
IBC
- ICA VBC Ia
Gambar 8. Diagram vector arus beban seimbang hubungan delta
Beban Tak Seimbang Terhubung Delta Beban tak seimbang yang direfresentasikan dengan tiga buah impedansi masing-masing Z1 . Z2 . Z3 yang dihubungkan delta yang dapat dicatu sumber hubungan delta maupun sumber hubungan bintang. Pada system tiga fasa hubungan delta terdapat dua macam arus, yaitu arus Line (IL) dan arus fasa (If). Arus Line yaitu arus yang mengalir pada Line penghantar terdiri dari Ia ; IB dan IC. Arus fasa yaitu arus yang mengalir didalam impedansi setiap fasa terdiri dari IAB; IBC dan IAB
A
a Ia
ICA
VCA
ZAC
VAB Ic C
c
ZAB IBC
IAB
B
ZBC VBC Ib b
Gambar 9. Beban tak seimbang terhubung Delta Untuk menghitung arus dan daya pada rangkaian 3 fasa hubungan delta digunakan metode arus lup yang akhirnya menghasilkan : Arus fasa :
IAB
VAB Vab ZAB ZAB
IBC
VBC Vbc ZBC ZBC
ICA
VCA Vca ZCA ZCA
Arus Line :
Ia IAB ICA
Ib IBC IAB
Ic ICA IBC
Daya pada Beban : Daya semu
: S3fasa = SAB + SBC + SCA = VAB(IAB)0 +VBC(IBC)0 + VCA(ICA)0
Daya nyata
: P3fasa= PAB + PBC + PCA
Dimana PAB= VABIAB cos AB PBC= VBCIBC cos BC PCA= VCAICA cos CA Daya Reaktif : Q3fasa= QAB + QBC + QCA Dimana QAB= VABIAB sin AB QBC= VBCIBC sin BC QCA= VCAICA sin CA
VCA
IC IB VAB
IA VBC
Gambar 10 Diagram vector arus beban Tak seimbang hubungan delta