Structural Analysis Exam Papers 41517

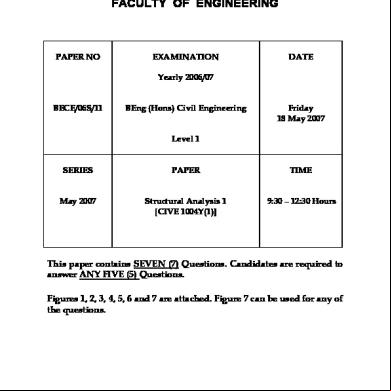
UNIVERSITY OF MAURITIUS FACULTY OF ENGINEERING

PAPER NO

EXAMINATION

DATE

Yearly 2006/07 BECE/06S/11

BEng (Hons) Civil Engineering

Friday 18 May 2007

Level 1 SERIES

PAPER

TIME

May 2007

Structural Analysis 1 [CIVE 1004Y(1)]

9:30 – 12:30 Hours

This paper contains SEVEN (7) Questions. Candidates are required to answer ANY FIVE (5) Questions. Figures 1, 2, 3, 4, 5, 6 and 7 are attached. Figure 7 can be used for any of the questions.

Question 1 A 2m long column is formed by welding together four steel plates to form a square hollow section with internal side dimensions of 250mm. The steel plates are 10mm thick. The steel hollow section is then filled with concrete. The column has to a load of 400 kN. Determine (a)

the stress in the concrete;

(b)

the stress in the steel;

(c)

the change in length of the column.

[14 marks]

[6 marks]

Modulus of elasticity of steel = 200 GN/m2 Modulus of elasticity of concrete = 20 GN/m2

Question 2 The beam ABCDE of Figure 1 is simply ed at A and D and loaded as shown. (a)

Calculate the reactions at the s A and D;

[6 marks]

(b)

Sketch the shear force and bending moment diagrams for the beam, showing the essential values. [14 marks]

Question 3 Figure 2 shows a steel post 6m high from which a 0.5m high by 1m long signboard is suspended. The post is made from a circular hollow section of external diameter = 200mm and thickness = 6mm and is fixed rigidly in the ground. The post has a shear modulus G = 80 kN/mm2. (a)

Determine the torsional stress in the post due to a wind pressure of 1kN/m2 acting normal to the signboard. [12 marks]

(b)

Estimate the rotation of the top of the post.

Page 1 of 2

[8 marks]

Question 4 Figure 3 shows a T-section which is 100mm wide and 125mm deep with a flange thickness of 25mm and web thickness of 12.5mm. (a)

Determine its Second Moment of Area about the horizontal axis through the centroid. [8 marks]

(b)

A built-in beam with the above section property spans over a length of 5m. If the maximum bending stresses of the beam are 50 MN/m2 in compression and 100 MN/m2 in tension, calculate the maximum uniformly distributed load (inclusive of the self weight of the beam) that the beam could . [12 marks]

Question 5 For the two-dimensional pin-ted frame shown in Figure 4, determine: (a)

The horizontal and vertical components of reaction at the s A and G; [6 marks]

(b)

The nature and values of axial force in each member of the frame, and indicate these on a sketch of the frame. [14 marks]

Question 6 The beam ABCDE of Figure 5 is simply ed at A and E and loaded as shown. Determine (a)

the deflection of the beam under the 20 kN load;

[10 marks]

(b)

the position and magnitude of the maximum deflection. Assume the flexural rigidity (EI) for the beam = 1.0 x 104 kNm2. [10 marks]

Question 7 The continuous beam ABC of Figure 6 carries the loads indicated. The flexural rigidity (EI) for span AB is 1 x 104 kNm2 and that for span BC is 2 x 104 kNm2. Draw the shear force diagram for the beam. [20 marks]

END OF QUESTION PAPER sg/

Page 2 of 2