Recta Imprimir 1111 t66a

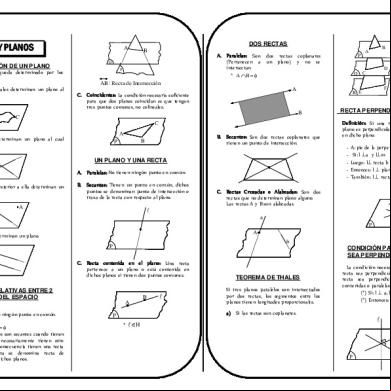
RECTAS Y PLANOS DETERMINACIÓN DE UN PLANO Un plano en el espacio queda determinado por los siguientes postulantes. 1.

Tres puntos no colineales determinan un plano al cual pertenecen. A

A

DOS RECTAS B

A. Paralelas: Son dos rectas coplanares (Pertenecen a un plano) y no se intersectan. * AB

Q S

D Q

A

C. Coincidentes: La condición necesaria suficiente para que dos planos coincidan es que tengan tres puntos comunes, no colineales.

C

C A

2. Dos rectas secantes determinan un plano al cual pertenecen.

B. Secantes: Son dos rectas coplanares que tienen un punto de intersección.

B

P

UN PLANO Y UNA RECTA A. Paralelas: No tienen ningún punto en común. B. Secantes: Tienen un punto en común, dichos puntos se denominan punto de intersección o traza de la recta con respecto al plano.

A

F

R E

B

B



B

A

AB : Recta de Intersección

C

3. Una recta y un punto exterior a ella determinan un plano.

P

AC BD  CE DF

RECTA PERPENDICULAR A UN PLANO Definición: Si una recta es perpendicular a un plano es perpendicular a todas las rectas contenidas en dicho plano. -

A: pie de la perpendicular. Si: l a y lm Luego: l recta b Entonces: l  plano P También: l  recta r

C. Rectas Cruzadas o Alabeadas: Son dos rectas que no determinan plano alguno. Las rectas A y B son alabeadas.



n

A

a

r

m

P

A

4. Dos rectas paralelas determinan un plano.

b

P

CONDICIÓN PARA QUE UNA RECTA SEA PERPENDICULAR A UN PLANO

C. Recta contenida en el plano: Una recta pertenece a un plano o está contenida en dichos planos si tienen dos puntos comunes. POSICIONES RELATIVAS ENTRE 2 FIGURAS DEL ESPACIO PLANOS A. Paralelos: No tienen ningún punto en común. * P // Q * PQ B. Secantes: Dos planos son secantes cuando tienen un punto común necesariamente tienen otro punto común, en consecuencia tienen una recta común, dicha recta se denomina recta de intersección entre dichos planos.

b

a



B A



TEOREMA DE THALES Si tres planos paralelos son intersectados por dos rectas, los segmentos entre los planos tienen longitudes proporcionales.

La condición necesaria y suficiente para que una recta sea perpendicular a un plano, es que dicha recta sea perpendicular a dos rectas secantes contenidas o paralelas a dicho plano. (*) Si: l  a; l  b (*) Entonces: l  plano P

a) Si las rectas son coplanares.

P



* H

a

P

b

PRÁCTICA DE CLASE

Teorema: Si una recta es perpendicular a dos rectas secantes contenidas en un plano; es perpendicular a todas las rectas contenidas en el plano determinado por las secantes.

 m n

b

a

1.Si por el pie de una recta perpendicular a un plano, se traza una segunda perpendicular a una recta contenida en dicho plano, el pie de la segunda perpendicular unida con cualquier punto de la recta perpendicular al plano, determina una recta perpendicular a la recta contenida en dicho plano. * l  plano P, m plano P, MN  m y Q  l

Q

* Luego: QN  m  n  m a b

* * * *

Q m ; n

MENOR DISTANCIA ENTRE DOS RECTAS ALABEADAS Es el segmento perpendicular a ambas rectas alabeadas. MN   , MN  m  MN es la menor distancia; es * decir la mínima distancia.

 m M

N

P

TEOREMA DE LAS TRES PERPENDICULARES n l Q Pie de la Penpendicular

P

m M

N

Observación: En cualquiera de los dos casos siempre x = 90°. a) * l  plano P * n  recta m *Luego: MN recta m * Es decir: x  90 b) * l  plano P * MN  recta m * Luego: n  recta m * Es decir: x  90

l

m P

xº

n

l

xº m P

M

a) Todo plano determinado por dos rectas paralelas a otro plano es siempre paralelo al otro plano. b) Si dos rectas son paralelas a un plano son siempre paralelas entre si. c) Toda recta paralela a uno de dos planos que se cortan perpendicularmente es siempre perpendicular al otro plano. d) Todo plano perpendicular a una recta situada en un plano es perpendicular al plano. e) Toda recta perpendicular a una recta contenida en un plano será perpendicular al plano.

2.- Si un plano es paralelo a una recta:

n

M N

¿Cuál de las siguientes proposiciones es verdadera?

N

a)Toda perpendicular a la recta será paralela al plano. b) Toda recta paralela al plano será paralela a la recta dada. c)Todo plano perpendicular al plano dado será paralela a la recta dada. d) Toda recta si es perpendicular al plano tendrá que ser perpendicular a la recta. e)Toda recta que es perpendicular al plano tendrá que ser paralela a la recta.

3.- .

4.-.¿Cuál de las siguientes proposiciones es falsa? a) Toda recta perpendicular a un plano perpendicular a cualquier recta contenida en el plano. b) Si una recta y un plano son perpendiculares todo plano que pasa por la recta es perpendicular al plano. c) Dos segmentos paralelos que se cortan a un plano forman con él, ángulos iguales. d) Por un punto de una recta sólo puede pasar un plano que sea perpendicular. e) N.A.

5.

¿Cuál de las siguientes proposiciones es falsa?

a) Si dos planos son paralelos las intersecciones de estos con un tercero son paralelas. b) Por una recta paralela a un plano sólo se puede trazar un plano perpendicular al primero. c) Dos planos perpendiculares a una misma recta son paralelos entre si. d) Toda recta paralela a un plano es paralelo a cualquier recta contenida en dicho plano. e) Si una recta M y un plano P son perpendiculares a una recta L la recta M y el plano P son paralelas entre si.

6.- ¿Cuál de las siguientes proposiciones es falsa? ¿Cuál de las siguientes afirmaciones es falsa?

a)Una recta y un plano perpendicular a una misma recta son paralelas. b) Es imposible trazar desde un punto dos perpendiculares distintas a un mismo plano. c) Una recta que es paralela a dos planos que se cortan es paralela a su intersección. d) Una recta que forman ángulos iguales con otras tres que se pasan por su pie en un plano es paralela a dicho plano. e) Si una recta es paralela a un plano entonces será paralela a todos los planos paralelos al plano dado.

a) Todos los planos paralelos a un plano dado son paralelos entre si. b) Todos los planos paralelos a una recta son paralelos entre si. c) Si un plano corta a una de tres rectas paralelas también corta a las otras dos. d) Si una recta es paralela a un plano la paralela trazada a dicha recta por un punto del plano estará contenida en el plano. e) Si un plano es paralelo a una recta toda paralela a la recta será paralela al plano.