P01 Besaran, Satuan Dan Vektor 6z173l

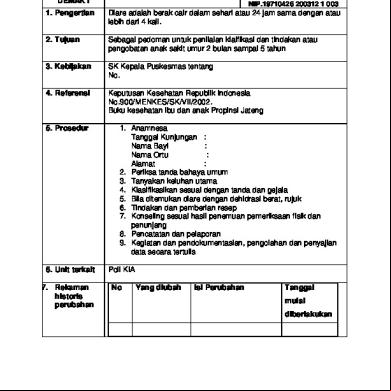
Fisika Dasar Session 1: Besaran, Satuan dan Vektor

(Untuk Teknik Sipil, Fakultas Teknik) Dr. Eng. Elin Yusibani Jurusan Fisika Universitas Syiah Kuala Last updated: September 2016

Kontrak perkuliahan Ujian Tengah Semester Ujian Akhir Semester Quiz Tugas

Materi Perkuliahan Besaran, satuan, vektor Kinematika gerak Dinamika gerak Energi dan Momentum Fluida Getaran dan Gelombang • Suhu dan Kalor • • • • • •

30 % 35 % 25 % 10 %

Referensi • Giancoli. D.C., 1995. Physics. Principles and Applications. 4th edition , Prentice Hall, New Jersey • Tipler, P.A., 1991, Fisika untuk Sains dan Teknik, Jilid 1, Penerbit Erlangga, Jakarta. • Serway/Faughn, College Physics, 7th editions • Halliday Resnick, Physics, 3rd editions (terjemahan) dll.

BESARAN DAN SATUAN Salah satu hal yang sangat penting dalam pengukuran di dalam fisika adalah satuan. Besaran: Sesuatu yang dapat diukur  dinyatakan dengan angka (kuantitatif) Contoh : panjang, massa, waktu, suhu, dll.

Satuan : Ukuran dari suatu besaran ditetapkan sebagai satuan. Contoh :  meter, kilometer  satuan panjang  detik, menit, jam  satuan waktu  gram, kilogram  satuan massa  dll. 3

Sistem satuan : ada 2 macam

1. Sistem Metrik : a. mks (meter, kilogram, sekon) b. cgs (centimeter, gram, sekon) 2. Sistem Non metrik (sistem British)

Sistem Internasional (SI)

Sistem satuan mks yang telah disempurnakan  yang paling banyak dipakai sekarang ini. Dalam SI : Ada 7 besaran pokok berdimensi dan 2 besaran pokok tak berdimensi

Satuan Pengukuran Satuan Pengukuran Sistem SI

CGS

BE

Panjang

m

cm

foot

Massa

kg

g

slug

Waktu

s

s

s

Konseptual

Besaran Pokok : besaran yang ditetapkan dengan suatu standar ukuran Besaran Turunan : Besaran yang dirumuskan dari besaran-besaran pokok

Besaran Fisika

Besaran Skalar : hanya memiliki nilai Matematis Besaran Vektor : memiliki nilai dan arah

7 Besaran Pokok dalam Sistem internasional (SI) NO

Besaran Pokok

Satuan

Singkatan

Dimensi

1

Panjang

Meter

m

L

2

Massa

Kilogram

kg

M

3

Waktu

Sekon

s

T

4

Arus Listrik

Ampere

A

I

5

Suhu

Kelvin

K

θ

6

Intensitas Cahaya

Candela

cd

j

7

Jumlah Zat

Mole

mol

N

Besaran Pokok Tak Berdimensi NO

Besaran Pokok

Satuan

Singkatan

Dimensi

1

Sudut Datar

Radian

rad

-

2

Sudut Ruang

Steradian

sr

-

Definisi standar besaran pokok Panjang - meter : Satu meter adalah panjang lintasan di dalam ruang hampa yang dilalui oleh cahaya dalam selang waktu 1/299,792,458 sekon.. sekon

Massa - kilogram : Satu kilogram adalah massa silinder platinum iridium dengan tinggi 39 mm dan diameter 39 mm.

Waktu - sekon Satu sekon adalah 9,192,631,770 kali periode (getaran getaran)) radiasi yang dipancarkan oleh atom cesiumcesium-133 dalam transisi antara dua tingkat energi (hyperfine level) yang terdapat pada tingkat dasar (ground state).

Besaran Turunan Besaran yang diturunkan dari besaran pokok. Contoh : a. Tidak menggunakan nama khusus NO

Besaran

Satuan

1

Kecepatan

meter/detik

2

Luas

meter 2

b. Mempunyai nama khusus NO

Besaran

Satuan

Lambang

1 Gaya

Newton

N

2 Energi

Joule

J

3 Daya

Watt

W

4 Frekuensi

Hertz

Hz

 Dimensi Cara besaran itu tersusun oleh besaran pokok. - Guna Dimensi : 1. Untuk menurunkan satuan dari suatu besaran 2. Untuk meneliti kebenaran suatu rumus atau persamaan - Metode penjabaran dimensi : 1. Dimensi ruas kanan = dimensi ruas kiri 2. Setiap suku berdimensi sama  Analisa Dimensi  

Suatu besaran dapat dijumlahkan atau dikurangkan apabila memiliki dimensi yang sama sama.. Setiap suku dalam persamaan fisika harus memiliki dimensi yang sama sama..

Besaran Turunan dan Dimensi NO

Besaran Pokok

Rumus

Dimensi

1

Luas

panjang x lebar

[L]2

2

Volume

panjang x lebar x tinggi

[L]3

3

Massa Jenis

massa volume

[m] [L]-3 [L] [T]-1

4

Kecepatan

perpindahan waktu

5

Percepatan

kecepatan waktu

6

Gaya

massa x percepatan

[M] [L] [T]-2

7

Usaha dan Energi

gaya x perpindahan

[M] [L]2 [T]-2

8

Impuls dan Momentum

gaya x waktu

[M] [L] [T]-1

[L] [T]-2

Faktor Penggali dalam SI Faktor Awalan Simbol

Faktor Awalan Simbol

1018

exa-

E

10-1

desi-

d

1015

peta-

P

10-2

senti-

c

1012

tera-

T

10-3

mili-

m

109

giga-

G

10-6

mikro-

µ

106

mega-

M

10-9

nano-

n

103

kilo-

k

10-12

piko-

p

102

hekto-

h

10-15

femto-

f

101

deka-

da

10-18

ato-

a

13

Unit dalam Tekanan

14

Besaran Skalar Besaran skalar adalah suatu besaran yang dapat digambarkan dengan satu angka yang mencirikan besar atau nilainya saja. Contoh: massa, panjang, waktu, rapat massa (density), tenaga (energi), dan suhu (temperatur) Perhitungan dengan skalar dapat dilakukan dengan menggunakan aturan aljabar biasa

Besaran Vektor Besaran vektor adalah suatu besaran yang selain memiliki nilai juga harus memiliki arah. Dengan suatu konvensi, panjangnya suatu gambar panah vektor sebanding dengan besarnya vektor tersebut. contoh: kecepatan, percepatan, jarak

Penjumlahan Vektor, metode Geometris Panjang anak panah dipilih sebanding dengan besar (magnitude) vektor dan arah anak-panah, yang ditunjukkan oleh arah ujungnya (kepalanya), menyatakan arah vektor Dalam penulisan vektor : A  Huruf tebal  A  Anak panah diatas A  Besar vektor

b a

a b

    a b  b a Sifat komutatif vektor

Aturan: Pada diagram yang telah disesuaikan skalanya, mula-mula diletakkan vektor pergeseran a; kemudian gambarkan vektor b dengan pangkalnya terletak pada ujung a, dan akhirnya kita tarik gars dari pangkal a ke ujung b yang menyatakan vektor hasil penjumlahan (a+b) Simbol + memiliki arti yang sama sekali berbeda dengan arti penjumlahan dalam ilmu aljabar skalar biasa, operasi ini merupakan operasi vektor 18

      d  (e  f )  ( d  e )  f     d e  f

e f

d

Sifat asosiatif vektor Kedua hukum (komutatif dan asosiatif) bagaimanapun urutan ataupun pengelompokkan vektor dalam penjumlahan, hasilnya tidak akan berbeda, dalam hal ini penjumlahan vektor dan skalar memenuhi aturan yang sama 19

Pengurangan Vektor b -b

    C  B  C  ( B) Operasi pengurangan vektor dapat dimasukkan ke dalam aljabar dengan mendefiniikannegatif suatu vektor sebagai sebuah vektor lain yang besarnya sama, tetapi arahnya berlawanan

Penjumlahan Vektor, metode Analitik y

a

φ

x

a  a x ˆi  a y ˆj a x  a cos  a y  a sin  a  a x2  a y2 I,j dan k adalah vektor satuan a

Untuk penjumlahan vektor dalam dua dimensi, metode geometris cukup memadai, tetapi untuk kasus tiga-dimensi seringkali kurang menguntungkan, cara lain adalah menggunakan metode analitik, termasuk disini penguraian vektor kedalam komponen-komponennya dalam suatu sistem koordinat tertentu Untuk mencari komponennya tidak perlu pangkal vektor terletak pada titik asal sistem koordinat, asal sudutnya terhadap sumbu koordinat dijaga tetap, komponennya tidak akan berubah

Perkalian Vektor Perkalian dot produk (hasil skalar)

A  iˆAx  ˆjAy  kˆAz ; B  iˆBx  ˆjB y  kˆBz A  B  Ax Bx  Ay B y  Az Bz A  B  AB cos  Perkalian cross Product (hasil vektor)

B  iˆBx ; C  iˆC x  ˆjC y

 

 

Aturan tangan kanan (sekrup)



B  C  iˆ  iˆ Bx C x  iˆ  ˆj Bx C y  0 Bx C x  kˆ Bx C y  kˆBx C y B  C  BC sin  22

Strategi Menangani Penjumlahan Vektor dengan menggunakan komponennya • Untuk setiap vektor yang akan dijumlahkan, tentukan dulu komponen-komponennya relatif terhadap koordinat yang digunakan. • Berilah tanda positif maupun negatif, untuk arah vektor berdasarkan sumbu positif maupun negatif koordinat yang digunakan. • Jumlahkan secara aljabar masing-masing komponen. • Gunakan komponen-komponennya secara Phytagoras untuk mencari besar vektornya. • Gunakan inversi sin, cos, atau tan untuk menentukan arah dari vektor tersebut.

Diferensiasi Vektor

A  iAx  jAy  kAz Bila A adalah fungsi dari t , maka diferensiasi dari A adalah dAy dAx dA dA i j k z dt dt dt dt d aA  da A  a dA dt dt dt d  A  B   A  dB  dA  B dt dt dt d  A  B   A  dB  dA  B dt dt dt Dalam kasus mekanika kita ketahui bahwa

posisi : r  ix  jy  kz dr dx dy dz i  j k dt dt dt dt dv d 2x d2y d 2z percepatan : a  i 2  j 2 k 2 dt dt dt dt kecepatan : v 

25