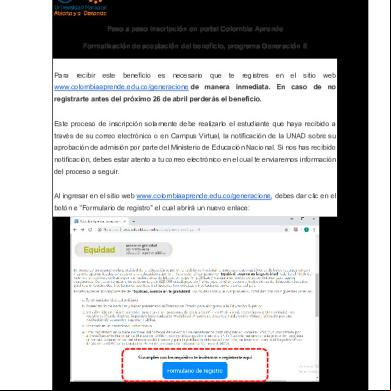
Paraboloide Elíptico 6z341z

PARABOLOIDE ELÍPTICO Es la superficie que se ha creado al deslizar una parábola vertical con la concavidad hacia abajo, a lo largo de la otra, perpendicular a la primera; las secciones horizontales son elipses mientras que las verticales son parábolas.

Definición Se denomina Paraboloide Elíptico a la superficie que en un sistema de coordenadas cartesianas se determina por la ecuación:

Las secciones de la cual son parabólicas o elípticas. El caso de revolución se obtiene haciendo girar una parábola alrededor de su eje de simetría y resulta ser el lugar geométrico de los centros de las esferas que pasan por un punto y son tangentes a un plano. Características El punto que coincide con el origen de coordenadas se llama vértice del paráboloide. Si la figura no coincide con el origen de coordenadas en el vértice entonce la ecuación es:

Las secciones que se obtienen al cortar la figura por planos con el eje Oz son parabolas. Las secciones que se obtiene al corta la figura por planos con el eje Oz son elipses.

Cuando a= b es el paraboloide elíptico es un Paraboloide en Revolución.

Aplicación Tiene la forma de las llamadas antenas parabólicas. Entre otros usos de origen cotidiano. Tiene la propiedad de reflejar (en caso de tener una superficie reflectante) la luz hacia un punto.

La ecuación implícita del paraboloide de sección circular de vértice (0,0,0) a lo largo del eje z es:

Como se deduce a partir de la ecuación para representar un paraboloide de sección circular a lo largo del eje z tomamos la ecuación de un cilindro con radio variable igual a \sqrt{z} (en vez de radio r fijo). Para que el paraboloide tenga sección elíptica tomamos la ecuación de un cilindro elíptico, es decir:

En este caso, a y b son los semiejes de la sección elíptica del paraboloide y c hace que el paraboloide sea más ancho o más estrecho. Para representar el paraboloide elíptico con vértice (x_0,y_0,z_0) restamos cada una de las coordenadas del centro a x,y y z respectivamente. La ecuación queda así:

Si queremos representar el paraboloide a lo largo de otro eje simplemente jugamos con los cuadrados. En la ecuación deben aparecer dos términos al cuadrado y uno elevado a uno y la ecuación debe estar igualada a cero. La variable que no está elevada al cuadrado es la que nos dice el eje del paraboloide. Además controlamos si el paraboloide aumenta de radio en el sentido positivo del eje o en el sentido negativo poniendo un más o un menos delante de la variable que no lleva el cuadrado. Por ejemplo, esta es la representación del paraboloide elíptico de ecuación