Ejercicios De Prueba De Independencia 6f434j
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Ejercicios De Prueba De Independencia as PDF for free.
More details 6z3438
- Words: 594
- Pages: 4
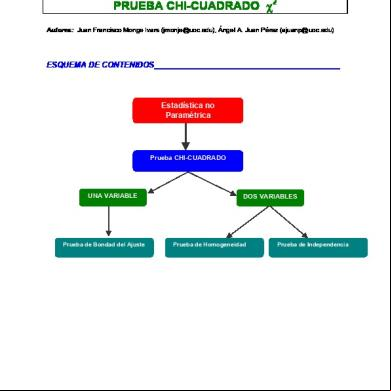
Prueba de independencia
Ejercicios de prueba de Independencia. Tabla de Contingencia En una encuesta pre-electoral realizada a 500 personas se obtuvo la siguiente Distribución en función de sus edades y de su intención de voto: Edad 18 – 35
35 – 50
50 o más
40 70 60 30
60 90 35 15
Partido A B C D
10 15 45 30
Compruebe la hipótesis a un nivel de confianza del 95% Solución: Paso 1. Redactar las hipótesis (Nula y Alternativa) La hipótesis Nula siempre se redacta en términos de independencia: H0: La intención de voto es Independiente de la edad de las personas. H1: La intención de voto depende de la edad de las personas. Paso 2. Determinar los grados de libertad G.L. = (Filas -1)*(Columnas -1)
Las Filas son horizontales y las Columnas verticales. Sólo se cuentan las celdas internas donde están los datos.
G.L.= (4-1)*(3-1) = 6 Paso 3. Determinar el punto Crítico Χ2 (GL;α) Buscamos en la tabla de la distribución Chi-cuadrado con 6 grados de libertad por el lateral y en la parte superior de la tabla el nivel de significación de 0,05. (α=1-0,95 = 0,05) encontramos que el valor crítico es. Χ2 (6; 0,05) = 12,592
Χ2 (6; 0,05) = 12,592
Prueba de independencia
Paso 4. Calcular las Esperanzas
Edad 18 – 35
35 – 50
50 o más
40 70 60 30 200
60 90 35 15 200
Total
Partido
A B C D Total
10 15 45 30 100
O
E
10 15 45 30 40 70 60 30 60 90 35 15 500
22 35 28 15 44 70 56 30 44 70 56 30 500
6,55 11,43 10,32 15,00 0,36 0 0,29 0 5,82 5,71 7,88 7,50 70,26
110 175 140 75 500
Supera al punto crítico (70,26 > 12,592)
Paso 5. Tomar la decisión. Como el valor del estadístico es mayor que el valor crítico se rechaza la hipótesis nula con un 95% de confianza o un 5% de significación.
Prueba de independencia
Ejercicio de Bondad de Ajuste La distribución del número de entrevistas conseguidas por los 56 alumnos que participaron en el proyecto fue la siguiente: No. De Entrevistas 0 1 2 3 4
No. De Alumnos 6 16 23 9 2
Compruebe la hipótesis a un nivel de significación del 95% Solución: Paso 1. Redactar las hipótesis (Nula y Alternativa) La hipótesis Nula siempre se redacta como una afirmación del patrón esperado: H0: Todos los estudiantes tienen la misma probabilidad de conseguir el mismo número de entrevistas. H1: No Todos los estudiantes tienen la misma probabilidad de conseguir el mismo número de entrevistas. Paso 2. Determinar los grados de libertad G.L.= Clasificaciones -1 G.L.= No. De entrevistas -1 G.L.= 5-1 = 4 Paso 3. Determinar el punto Crítico Χ2 (GL;α) Buscamos en la tabla de la distribución Chi-cuadrado con 4 grados de libertad por el lateral y en la parte superior de la tabla el nivel de significación de 0,05. Encontramos que el valor crítico es 9,49
Prueba de independencia
Paso 4. Calcular las Esperanzas Como el patrón esperado es que todos los estudiantes realicen el mismo número de entrevistas se calcula un promedio entre las observaciones y el número de entrevistas.
No. De Entrevistas
0 1 2 3 4
O
E
6 16 23 9 2 56
11,2 11,2 11,2 11,2 11,2 56
2,41 2,06 12,43
Paso 5. Tomar la decisión Se rechaza la hipótesis nula con un 5% de significación.
La sumatoria hasta aquí ya demuestra que sobrepasa el punto crítico lo que indica que se rechaza la H0
Ejercicios de prueba de Independencia. Tabla de Contingencia En una encuesta pre-electoral realizada a 500 personas se obtuvo la siguiente Distribución en función de sus edades y de su intención de voto: Edad 18 – 35
35 – 50
50 o más
40 70 60 30
60 90 35 15
Partido A B C D
10 15 45 30
Compruebe la hipótesis a un nivel de confianza del 95% Solución: Paso 1. Redactar las hipótesis (Nula y Alternativa) La hipótesis Nula siempre se redacta en términos de independencia: H0: La intención de voto es Independiente de la edad de las personas. H1: La intención de voto depende de la edad de las personas. Paso 2. Determinar los grados de libertad G.L. = (Filas -1)*(Columnas -1)
Las Filas son horizontales y las Columnas verticales. Sólo se cuentan las celdas internas donde están los datos.
G.L.= (4-1)*(3-1) = 6 Paso 3. Determinar el punto Crítico Χ2 (GL;α) Buscamos en la tabla de la distribución Chi-cuadrado con 6 grados de libertad por el lateral y en la parte superior de la tabla el nivel de significación de 0,05. (α=1-0,95 = 0,05) encontramos que el valor crítico es. Χ2 (6; 0,05) = 12,592
Χ2 (6; 0,05) = 12,592
Prueba de independencia
Paso 4. Calcular las Esperanzas
Edad 18 – 35
35 – 50
50 o más
40 70 60 30 200
60 90 35 15 200
Total
Partido
A B C D Total
10 15 45 30 100
O
E
10 15 45 30 40 70 60 30 60 90 35 15 500
22 35 28 15 44 70 56 30 44 70 56 30 500
6,55 11,43 10,32 15,00 0,36 0 0,29 0 5,82 5,71 7,88 7,50 70,26
110 175 140 75 500
Supera al punto crítico (70,26 > 12,592)
Paso 5. Tomar la decisión. Como el valor del estadístico es mayor que el valor crítico se rechaza la hipótesis nula con un 95% de confianza o un 5% de significación.
Prueba de independencia
Ejercicio de Bondad de Ajuste La distribución del número de entrevistas conseguidas por los 56 alumnos que participaron en el proyecto fue la siguiente: No. De Entrevistas 0 1 2 3 4
No. De Alumnos 6 16 23 9 2
Compruebe la hipótesis a un nivel de significación del 95% Solución: Paso 1. Redactar las hipótesis (Nula y Alternativa) La hipótesis Nula siempre se redacta como una afirmación del patrón esperado: H0: Todos los estudiantes tienen la misma probabilidad de conseguir el mismo número de entrevistas. H1: No Todos los estudiantes tienen la misma probabilidad de conseguir el mismo número de entrevistas. Paso 2. Determinar los grados de libertad G.L.= Clasificaciones -1 G.L.= No. De entrevistas -1 G.L.= 5-1 = 4 Paso 3. Determinar el punto Crítico Χ2 (GL;α) Buscamos en la tabla de la distribución Chi-cuadrado con 4 grados de libertad por el lateral y en la parte superior de la tabla el nivel de significación de 0,05. Encontramos que el valor crítico es 9,49
Prueba de independencia
Paso 4. Calcular las Esperanzas Como el patrón esperado es que todos los estudiantes realicen el mismo número de entrevistas se calcula un promedio entre las observaciones y el número de entrevistas.
No. De Entrevistas
0 1 2 3 4
O
E
6 16 23 9 2 56
11,2 11,2 11,2 11,2 11,2 56
2,41 2,06 12,43
Paso 5. Tomar la decisión Se rechaza la hipótesis nula con un 5% de significación.
La sumatoria hasta aquí ya demuestra que sobrepasa el punto crítico lo que indica que se rechaza la H0