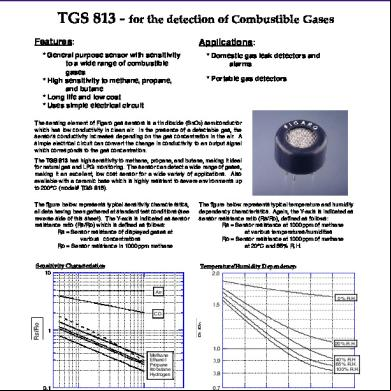
Cours Gaz 2r5529

‫بسم هللا الرحمان الرحيم‬

‫‪1‬‬

M. BELLAHCENE UFR: Gas, Refining & Petrochemistry

2

Séances Régulières

-Lundi : -Mardi :

13:30 - 16:30 13:30 - 16:30

Lieu : Amphi 5ème Etage

3

Contrôle 02 Examens:

01 mid term 40% 01 examen de synthèse 60%

4

Estimation Des Propriétés Physiques Des Hydrocarbures

5

Références T. H. Ahmed, ‘Hydrocarbon Phase Behavior’ , Contribution in Petroleum Geology & Engineering Vol. 7, Gulf Publishing Company, Huston, 1989.

T. H. Ahmed, ‘Hydrocarbon Phase Behavior’ , Contribution in Petroleum Geology & Engineering Vol. 5, Gulf Publishing Company, Huston, 1989. R. C. Reid, ‘The Properties of Gases and Liquids’ , Third Edition, McGraw Hill, New York, 1977.

J. M. Smith, ‘Introduction to Chemical Engineering Thermodynamics’ , Third Edition, McGraw Hill, New York, 1975. D. L. Katz et al., ‘Handbook of Natural Gas Engineering’ , McGraw Hill, New York, 1959. R. W. Gallant, C. L. Yaws, ‘Physical Properties of Hydrocarbons’ , V.1, Second Edition, Gulf Publishing Company, 1992. Gas Processors Suppliers Association, ‘Engineering Data Book’ , GPSA, 1974. C. U. Ikoku, ‘Natural Gas Engineering’ , PennWell Books, 1980 6

Introduction - Thermodynamique : systèmes fermés / ouverts. - Evolution des Propriétés : due à l’échange avec l’environnement.

- Description d’Etat : en déterminant ses propriétés (T, P, V, yi) - Compilation de données expérimentales de plusieurs espèces -Valeurs de propriétés indisponibles : Théorie, méthode d’estimation ou combination des deux - Equations Empiriques - Parfois inclure l’empiricisme dans des équations existantes telles

a   PV  nRT   P  2  V  b   RT V  

7

Types de Méthodes d’Estimations Une méthode d’estimation Idéal

1 – Donner des résultats physiques et thermodynamiques acceptables pour substances pures et mélanges pour toutes conditions 2 – Indiquer l’état 3 – Requiert peu d’information d’entrée 4 – Précise 5 – Temps de calcul court Methodes d’estimation : pas idéales mais donnent des résulats acceptables. Utiliser méthodes simples lorsque les valeurs approximatives sont acceptées. Preférence de données expérimentales.

8

Loi des Etats Correspondants D’aprés van der Waals

- Les propriétés dépendant des forces intermoléculaires sont liées aux propriétés critiques de la même manière pour tous les composés (Not perfect) - Deux substances sont dites dans des états correspondants quand leurs propriétées réduites sont les mêmes.s mêmes. - La déviation d’un gaz réel par rapport à la loi des gaz parfaits est la même pour différents gaz aux mêmes conditions correspondants de P et T . r

r

- C’est une base importante pour le développement de correlations et méthodes d’estimation. - Plus correcte/précise pour les substances physicochimiquement similaires. 9

AC : Liquide saturé BC : Vapeur saturée

Critical Po int C

Pr essure Liquid 

Liquid

Gas

Vapour

T1

A B

T2

Volume Comportement volumétrique d’une substance pure tel que prédit par l’Equation d’Etat (EE) de van der Waals

10

La loi des états correspondants telle qu’appliquée aux propriétés du méthane et l’azote. Valeurs experimentales : ○ Méthane, ● Azote.

11

Courbes d’Equilibre Liquide-Vapeur

12

Propriétés Physiques de Substances Pures

13

Constante des Gaz Parfaits R  8.314 J / ( g  mole) K  1.987 cal /( g  mole) K

 83.14 cm 3 . bar  / ( g  mole) K  82.05 (cm 3 . atm) /( g  mole) K  0.7302 (atm . ft 3 ) /(lb  mole)  R  10.73 ( psia . ft 3 ) / lb  mole)  R  1545 ( ft . lb f ) / (lb  mole)  R  1.987 Btu / (lb  mole)  R

14

Comportement de Gaz Parfaits Volume des molécules négligeable devant le volume du milieu où elles sont confinées, et pas de forces d’attraction ou de répulsion entre elles.

1. Gaz Purs Loi des gaz parfaits

ou

PV  n R T

 m  PV    RT  MW 

m P MW g   V RT 15

2. Mélanges de gaz parfaits

Pm Vm  R Tm

Décrits par la loi des gaz parfaits

(m  mélange)

Le comportement des mélanges est plus intéressant que celui des corps purs puisque en pratique les gaz existent et/ou sont utilisés le plus souvent sous forme de mélanges de composants d’ydrocarbures.

- fraction molaire

yi 

ni n



ni

n

i

i

- fraction massique

wi 

mi m



wi 

mi

m

ou i

i

- fraction volumique

Vi v  V

yi MWi  yi MWi i

yi 

wi / MWi 

 (w / MW ) i

i

i

Vi  Vi i

16

Exercice 1 Déterminer la composition en fraction massique

Composant

Fraction Molaire y i

C1

0.65

C2

0.10

C3

0.10

C4

0.10

C5

0.05

Exercice 2 Déterminer la composition en fraction molaire

Composant

Fraction Massique wi

C1

0.40

C2

0.10

C3

0.20

C4

0.20

C5

0.10

17

Propriétés de Mélanges Gazeux Parfaits Poids moléculaire Apparent

MWa   yi MWi i 1

Volume Standard

(1) R Tsc Vsc  Psc

1 mole PSC  14.7 psia (1 atm) TSC  60  F

(15.6 C )

R  10.73 psia . ft 3 . (lb  mole) 1 .  R 1





1 x 10.73 psia. ft 3 .(lb  mole) 1 .R 1 x (60  460) R Vsc  14.7  psia  VSC  379.4 scf ( s tan dard cubic fet )  379.4 ft 3 /(lb  mole18)

Masse Volumique

P MWa g  RT

Volume Spécifique

 

Densité (Specific gravity)

V RT 1   m p MWa  g

g 

g densité du gaz à temperature T et pression P  densité de l ' air à temperature T et pression P  air

Si l’air et un autre gaz se comportement idéalement, la densité du gaz est

 p MWa    R T   MWa  MWa g    p MWair  MWair 28.96   R T   19

Exercice Considérer un mélange gazeux idéal avec la composition suivante, à 1000 psia et 100 °F. Calculer a) le poids moléculaire apparent, b) la densité, c) la masse volumique, et d) le volume spécifique

Composant

yi

C1

0.75

C2

0.07

C3

0.05

C4

0.04

C5

0.04

C6

0.03

C7 a. 26.14 lbm/lb-mole b. γ = (26.14/28.96) = 0.903 c. ρ = [(1000x26.14)/(10.73x460)] = 4.35 lbm/ft3

0.02 20

Comportement de Gaz Réels Composants Purs Ce qui a été considéré pour les gaz parfaits (volume négligeable des molécules et pas d’attraction ou repulsion entre elles) n’est pas vrai pour les gaz réels, et c’est ce qui les fait dévier de la loi des gaz parfaits. Plusieurs équations d’états (EDE) ont été développées afin de corréler les variables P, V , T avec les mesures expérimentales, et d’exprimer une meilleure relation entre ces variables. P, V , T Un facteur de correction appelé Facteur de Compressibilité ou Facteur Z a été introduit dans l’équation des gaz parfaits

PV  ZnRT Compressibility factor

Va actual gas volume Z   Vi ideal gas volume

Gaz Parfait : Z 1; Z peut être sup érieur ou égale à 1 pour les gaz réels , dependant de T 21 , P , yi

Z Peut être déterminé expérimentallement : - Measurer volume à T et P - Résoudre l’EDE pour Z

PV  ZnRT

Z

Beaucoup de travaux expérimentaux ont conduit à l'établissement d'un rapport entre le facteur de compressibilité et la pression et température (voir figures ci dessous). Donc, actuellement, y a aucun besoin de travail expérimental puisque beaucoup d'information existent sur le changement de Z avec P, et T pour des corrélations basées sur la loi des états correspondants. La loi des états correspondants propose que tous les gaz auront le même comportement quand ils sont analysés en termes de pression réduite, volume réduit, et température réduite, ou autrement dit la déviation par rapport à la loi idéale de n'importe quel gaz réel est proportionnellement la même pour différents gaz quand ils sont dans les mêmes conditions correspondantes (conditions réduites). Propriétés réduites

P Pr  PC

Tr 

T TC

V Vr  VC

22

Méthane

Ethane

Diagramme de facteur de compressibilité 23

Propane

Diagramme de facteur de compressibilité

24

Exercice Calculer le facteur de compressibilité du Méthane, Ethane, et Propane, à pression et température réduites de 2 , et 1.6 respectivement. Solution Utiliser les tables de propriétés physiques pour trouver tout d’abord les propriétés critiques des gaz pour ensuite déterminer les pression et température absolues. Méthane

P  Pr .  PC  (2)(667.8)  1335.6 psia T  Tr  TC  (1.6)(116.63  460)  549.392 R

Ethane

A l’aide de P, T et la figure appropriée

Z  0.88

Propane

P  Pr .  PC  (2)(707.8)  1415.6 psia

P  Pr .  PC  (2)(616.3)  1232.6 psia

T  Tr  TC  (1.6)(90.09  460)  880.166 R

T  Tr  TC  (1.6)(206.01  460)  1065.616 R

Z  0.882

Z  0.886

Noter la similarité des facteurs Z

Efficacité du principe des états correspondants 25

Mélanges de gaz L’application du principe des états correspondants est basée sur l’observation stipulant que la compressibilité est une fonction universelle des pression et températures réduites. Pour les mélanges de gaz, Kay a introduit le concept de pseudo propriétés critiques à la place des propriétés critiques réelles.

Règle de mélange de Kay

y

PPC 

i

PC i



TPC 

i

yi TC i

i

And the reduced properties are called pseudo reduced properties

PP r 

 i

P P   yi PCi  PPC

TP r 



T T   yi TCi  TPC

i

26

Le facteur de compressibilité peut être généralisée avec suffisament d’exactitudes pour la plus part des besoins en intrduisant le concept des pseudo pression et temperatures réduites. Standing et Katz ont presenté en 1942 un facteur de compressibilité généralisé comme montré sur la figure.

- Fiable pour les gaz naturels doux ayant une teneur faible de composants non hydrocarbonés (CNH). - Corrélations les plus largement ises - Bon pour des mélanges de gaz de MW < 40 - Ne peut pas être appliqué pour des gaz ou des vapeurs avec plus de 2% d'H2S et/ou CO2 ou plus de 20 % de N2 (d'autres méthodes sont employées)

Diagramme de Standing et Katz Facteur de compressibilité des gaz naturels

27

Si la composition n’est pas connue : PPC , TPC peuvent être prédits à l’aide



Brown et al. ont d éveloppée une méthode graphique donnant une approximation satisfaisante des pseudo pression et température critiques de gas quand uniquement la densité du gaz est connue

Mathematical correlation Mélanges de gaz naturels

TPC R  168  325  g  12.5  g2 PPC  psia   677 15.0  g  37.5  g2 Mélanges de condensats (liquide)

TPC R  187  330  g  71.5  g2

PPC  psia   706  51.7  g  11.1 g2 28 Corrélation graphique des pseudo propriétés critiques des gaz naturels

Exercice Déterminer la masse volumique du mélange gazeux suivant. Considérer le mélange parfait at 1000 psia et 100 °F.

Composant

yi

C1

0.75

C2

0.07

C3

0.05

C4

0.04

C5

0.04

C6

0.03

C7

0.02 29

Solution Composant

yi

MWi

y i MWi

TC i  R 

y i TC i

C1

0.75

16.04

12.030

343.5

257.6

673

504.7

C2

0.07

30.07

2.105

550.1

38.5

708

49.6

C3

0.05

44.10

2.205

666.2

33.3

617

30.9

C4

0.04

58.12

2.325

765.6

30.6

551

22.0

C5

0.04

72.15

2.886

847.0

33.9

485

19.4

C6

0.03

86.18

2.585

914.6

27.4

434

13.0

C7

0.02

100.21

2.004

972.8

19.5

397

7 .9

MWa  26.14  m   RT PV  ZnRT  Z  MW a  

Ensuite, calculer

PPr 

TPC  440.8

 

V ZRT  m P MWa

P 1000   1.54 PPC 647.5

Figure ci dessus : Z = f(propriétés réduites)

Finalement :

PC i  psia 

et

PPC  647.5

g 

TPr 

y i PCi

1





P MWa ZRT

T (100  460)   1.27 TPC 440.8

Z  0.725

1000 x 26.14 g   6.00 lb / ft 3 0.725 x 10.73 x 560

30

Exercice Recalculer la masse volumique, de l’exercice précédent, en estimant les pseudo propriétés réduites.

Solution 1. Calculer la densité du mélange gazeux

g 

MWa 26.14   0.903 29.96 29.96

2. Déterminer les pseudo propriétés critiques





TPC  168  325 x 0.903  12.5 x 0.9032  451  R





PPC  677  15.0 x 0.903  37.5 x 0.903 2  660 psia 3. Trouver les propriétés pseudo réduites

TPr 

560  1.24 451

PPr 

1000  1.52 660

4. Déterminer Z à partir de la figure utilisée précédement

Z  0.69

5. Finalement, calculer la masse volumique

g 

1000 x 26.14  6.30 lb / ft 3 0.69 x10.73 x 560

31

Effet de composants non hydrocarbonés (CNH) sur Z Les gaz naturels contiennent souvent des CNH notamment: CO2 , N2 , et H2S. Les gaz hydrocarbonéssont classés comme suit: - doux : pas de sulphide d’hydrogène - acides : si [H2S] = 1 grain / 100 ft3

[NHC] ≤ 5% : la précision n’est pas sérieusement affectée [NHC] > 5% : jusqu’à 10 % Z peut être érroné, donc des corrections sont obligatoires.

32

Correction pour CNH Les CNH ont un net effet sur les propriétés des gaz puisque leur facteur de compressibilité a un comportement différent de celui des gaz doux. D’après Wichert et Aziz Ont développé une méthode précise pour le calcul de Z des gaz acides contenant jusqu’à 85% de composants acidiques, et ceci à l’aide de diagrammes standard du facteur de compressibilité des gaz. Ont défini un pseudo facteur d’ajustement de température critique  pour ajuster (corriger) les pseudo propriétés critiques du mélange gazeux acide.

  f ( CO2 , H 2 S )

' PC

T

 TPC  

and

PPC'

PPC TPC'  TPC  B(1 B) 

  120 ( A0.9  A1.6 )  15 ( B 0.5  B 4.0 ) [R]

A  yH 2 S  yCO 2

A : sum of mole fractions of CO2 and H2S in mixture 33 B : mole fraction of H2S

Les étapes de calcul et d’introduction de



dans les calcul du facteur Z

Etape 1: Calculer les pseudo propriétés critiques du mélange de gaz Etape 2: Déterminer le facteur de correction  (à partir du diagramme ci dessous ou le calculer à l’aide des équations ci dessus) Etape 3: Corriger PPC et

TPC (calculés à l’étape 1)

Etape 4: Calculer les pseudo propriétés réduites Etape 5: Lire le facteur de compressibilité à partir de la figure de Standing et Katz.

34

 Facteur de correction de la pseudo température critique, in °R.

35

Exercice Déterminer la masse volumique d’un mélange gazeux acide, à 1000 psia et 110 °F , ayant la composition ci dessous et considéré idéal.

a. Sans correction due à la présence des CNH b. En utilisant la méthode de correction de Wichert-Aziz c. Que concluez-vous?

Composant

yi

CO2

0.10

H2 S

0.20

N2

0.05

C1

0.63

C2

0.02 36

Solution yi

MWi

yi MWi

PC i  psia  yi PC i

TC i  R 

yi TC i

CO2

0.10

44.01

4.401

1071

107.1

547.57

54.757

H2 S

0.20

34.08

6.816

1306

261.2

672 .37

134 .474

N2

0.05

28.01

1.401

493

24.65

227.29

11.365

C1

0.63

16.04

10.105

667

420 .714

343.06

216 .128

C2

0.02

30.07

0.601

707.8

14.156

549.78

11.00

Composant

MWa  23.324

827.82

427.72

Calculer la densité

23.324 g   0.8054 28.96 Ensuite, déterminer à partir de la table ci dessus

PPC  827.82 psia TPC  427.72 R 37

1. La masse volumique sans corrections

PPr 

1000  1.208 827.82

TPr 

570  1.333 427.72

A l’aide des pseudo propriétés réduites ci-dessus et la figure de Standing-Katz, le facteur Z est Z  0.820

Ensuite, calculer la masse volumique à l’aide de l’équation

g 

1000 x 23.324  4.651 lb / ft 3 0.82 x10.73 x 570

1. La masse volumique avec corrections

B  yH 2 S  0.2

A  yCO2  yH 2 S  0.1  0.20  0.30

Déterminer le facteur de correction

  120 ( 0.30 0.9  0.301.6 )  15 ( 0.20 0.5  0.20 4.0 )  29.86R ensuite, corriger la pseudo température critique

TPC'  427.72  29.86  397.86  R Après cela, calculer la pseudo pression critique corrigée

PPC' 

827.82 x 397.86  727.07 psia 427.72  0.2 x (1 02) x 29.86

38

la pseudo pression reduite est alors égale à

P 1000   1.375 ' PPC 727.07

PPr 

Et la pseudo température reduite

TPr 

T 570   1.433 TPC' 397.86

finalement, à l’aide des pseudo properties reduites ci-dessus et la figure de Standing-Katz, Le nouveau facteur de compressibilité est

Z  0.837 Et la masse volumique correspondante est

g 

1000 x 23.324  4.56 lb / ft 3 0.837 x10.73 x 570

Il y a environ 2 % d’erreur entre les valeurs corrigée et non corrigée. 39

-Carr, Kobayashi, et Burrows ont proposé une procédure simplifiée pour corriger les pseudo propriétés critiques des gaz naturels contenants des CNH. -La méthode est avantageuse lorsque la composition du mélange de gaz est inconnue. -Connaissant la densité du mélange gazeux, déterminer les pseudo température et pression critiques à l’aide de la dernière figure. Ensuite, ajuster, à l’aide des équations suivantes, les pseudo propriétés critiques estimées.

TPC' R  TPC  80 yCO2  130 y H 2S  250 y N2 PPC'  psia   PPC  440 yCO2  600 y H 2S  170 y N2

40

Correction pour les gaz à MW élevé Aucun mélange de MW > 40 n’a été considéré dans la réalisation du diagramme, donc la figure ne peut être applicable aux mélange gazeux de MW > 40 .

Sutton à observé que les déviations sont associés aux mélanges ayant des concentrations élevées d’ heptanes-plus (C7+) , et proposa que les déviations peuvent être minimisées en utilisant les règles de mélange développées par Stuart et al., et des facteurs empiriques de correction liés à la présence de concentration d’heptanes-plus dans le mélange gazeux.

Diagramme de Standing-Katz facteur de compressibilité

41

Approche de correction proposée 1. Calculer les paramètres 0.5  TC   2   TC   1 J   yi      yi    3  i  PC  i  3  i  PC  i 

 K    yi i  

2

 TC    0.5    PC i 

Paramètre de corrélation de Stewart-Burkhardt-Voo

Paramètre de corrélation de Stewart-Burkhardt-Voo

 R / psia

R / psia  0.5

2. Déterminer les paramètres de correction

 J  0.6081FJ  1.1325 FJ 2  14.004 FJ yC  64.434 FJ yC2 7

7

2

0.5 1   TC  2   TC   FJ   y     y    3   PC  C 3   PC     C7  7

 T 

 K   C0.5  (0.3129 yC  4.8156 yC2  27.3751 yC3 )  PC C 7

7

7

7

Température en [° R] , et Pression en [psia]

3. Corriger les paramètres J and K

K  K  K '

J '  J  J 42

4. Déterminer les pseudo température et pression critiques ajustées

 K  

' 2

TPC

J

T

'

PPC

TPC  ' J

P

5. Utiliser PC et PC calculées et suivre la procédure normale de Standing et Katz pour déterminer le facteur de compressibilité.

43

Analyse Mathématique du Diagramme de Standing-Katz du Facteur de Compressibilité Parfois il est plus pratique d’utiliser des équations mathématiques simples pour des calculs directs du facteur de compressibilité. Méthode de Papay - empirique - 4.8 % erreur

P Z  1  Pr TPr

  PPr  0 . 36748758  0 . 04188423    TPr

  

Il existe d’autres méthodes plus compliquées nécissitant des solutions numériques.

44

La Compressibilité des gaz naturels - Indispensable dans les problèmes de reservoir engineering - Plus importante que celle des liquides - Pour un liquide elle est suffisament faible pour être négligée.

La compressibilité isotherme d’un gaz est le changement de volume par unité de volume par unité de changement de la pression

1  V  Cg     V  P T

n RT Z V  P Cg 

in

1/ unit pressure 

Differentiating

1  V     nRT   P T P

 Z  Z     2  P  P 

1 1  Z     P Z  P T

Gasz Idéal Z = 1 :

Cg 

1 P

45

En termes de pseudo propriétés

Cg 

Multiplier l’équation par

 1 1 Z    PPr PPC Z   PPr PPC  T Pr

PPC

C g PPC  Cr 

1 1  Z     PPr Z   PPr  T Pr

Qui est la pseudo compressibilité reduite isotherme et définie comme

Cr  C g PPC (Z / PPr )TPr peuvent être calculées à partir de la pente de l’isotherme TPr Les valeurs de du diagramme de Standing-Katz du facteur de compressibilité à la valeur d’intérêt.

46

Exercice Déterminer la compressibilité isotherme d’un mélange gazeux (composition ci dessous) à 1000 psia et 100°F, en considérant a. Un comportement idéal (parfait) b. Un comportement de gaz réel

Composant

yi

C1

0.75

C2

0.07

C3

0.05

n  C4

0.04

n  C5

0.04

C6

0.03

C7

0.02

47

Solution 1.

Comportement idéal Utiliser dirctement l’équation de Cg

2.

Cg 

1 1   10 3 psia 1 P 1000

Gaz réel

a. Calculer

PPC  647.5 psia

b. Ensuite

PPr 

1000  1.54 647.5

TPC  440.8 R TPr 

(100  460)  1.27 440.8

c. A l’aide de la figure de Standing-Katz on obtient Z  0.725

et la pente

 Z     0.17    P Pr TPr 1.27  d. Déterminer la pseudo compressibilité reduite isotherme

Cr 

1  1    ( 0.17)  0.8808 1.54  0.725 

e. Finallement, calculater la compressibilité du gaz

Cg 

Cr 0.8808   1.361 x10 3 psia 1 PPC 647.5

48

L’exemple peut être résolu à l’aide du diagramme de Trube

Cr  0.90 Cg 

Cr 0.90   1.390 x10 3 psia 1 PPC 647.5

Il existe d’autres méthode plus compliquée telle que la méthode de Mattar-Brar-Aziz (n’est pas donnée ici)

Pseudo compressibilité reduite des gaz naturels Diagramme de Trube

49

Facteur Acentrique Un troisième paramètre  , le facteur acentrique développé par K. S. Pitzer en 1955, comme paramètre de corrélation pour caractériser la non sphéricité d'une molécule. Il a été largement accepté et considéré afin de surmonter certaine limites du principe des états correspondant. Définition du facteur acentrique

   log 10 Prsat T

r

Prsat  

Dépendence approximative de T = f(pression de vapeur)

Facteur acentrique moyen d’un mélange

 0.7

1

Pv PC

est zéro pour l’argon, krypton, et xenon

D’après la théorie de Pitzer (états correspondants basés sur les 3 paramètres) tous les fluides ayant la même valeur  ont la même valeur du facteur Z une fois comparés aux mêmes Pr et Tr .

m   yi i 50

Pression de vapeur

(sera discutée en détails)

La pression de vapeur d’une substance est la pression exercée par sa phase vapeur en equilibre avec sa phase liquide ou solide à une température donnée.

Po int Critique C

P Pr ession P

Liquide 

Liquide

Gas

Vapeur

T1

A

B

T2

T Correlation

Volume

T   T  ln PV  19 1  b   8.5 ln  b  T  T 

51

52

Pression de vapeur à basse température d’hydrocarbures légers

Pr ession de Vapeur [ psia ]

Temperature 53 F  Pression de vapeur de composants d’hydrcarbures

Viscosité Résistance à l’écouement, égale au rapport de la contrainte de cisaillemnt (force tangentielle/unité de surface) sur le taux de cisaillement (gradient de vitesse local):

 

Fonction de la forme

 

 g   g ( P, T , yi )

Procédure de calcul Carr, Kobayashi, et Burrows ont développé des corrélations graphiques pour estimer la viscosité des gazs naturels en fonction de la pression, temperature et densité du gaz.

1. Chercher PPC et MWa , et corriger les si [NHC] > 5 moles pour cent 2. Utiliser la figure ci dessous pour déterminer la viscosité du gaz naturel à 1 atm et temperature d’intérêt. Cette viscosité, nommée  1 , doit être corrigée à cause de la présence des CNH (à l’aide des médaillons des figures). Les fractions des CNH tendent à augmenter la viscosité de la phase gazeuze, mathématiquement

 1   1 u   CO   H S   N 2

3. Déterminer les pseudo pression et temperature reduites

2

2

54

4. Déterminer



g

/  1

à l’aide des pseudo propriétés reduites

 g = viscosité du gaz aux conditions désirées.

Corrélation de rapport de viscosité de Carr 5. Finalement, calculater  g à l’aide de

g

g  1 1

55

Corrélation de viscosité atmosphérique du gaz de Carr 56

. . .

G: specific gravity

Correction de viscosité due à la présence de H2S

57

Correction de viscosité due à la présence de CO2

58

Correction de viscosité due à la présence de N2

59

60

Viscosité de gaz en fonction de différentes variables

61

Viscosité de gaz en fonction de différentes variables

Herning et Zipperer ont proposé l’équation ci dessous pour estimer la viscosité de mélanges gazeux n

m 

 i 1 n

yi MWi

i

y i 1

i

MWi

62

Exercice Déterminer la viscosité du mélange gazeux à 3500 psia et 200 °F.

Composant

yi

N2

0.05

CO2

0.05

H2S

0.02

C1

0.80

C2

0.05

C3

0.03

63

Solution Dans ce cas il y a une correction à effectuer due à la présence des CNH.

1. Calculer :

MWa

g

MWa 

 y MW i

PPC i

TPC

 19.97

i

g 

g density of gas at temperature T and pressure P 19.97    0.689 density of air at temperature T and pressure P  air 28.96

TPC  168  325  g  12.5  g2  380.43 R

PPC  677 15.0  g  37.5  g2  665.11 psia 2. Corriger les pseudo propriétés critiques calculer en 1. (à cause de la présence des CNH)

TPC'  TPC  80 yCO2  130 y H 2S  250 y N2 

TPC'  380.43  80 x 0.05  130 x 0.02  250 x 0.05  366.53  R

PPC'  PPC  440 yCO2  600 yH 2 S  170 yN 2 PPC'  665.11  440 x 0.05  600 x 0.02  170 x 0.05  690.61 64 psia

3. A l’aide de la dernière figure de Carr, estimer la viscosité non corrigée à 1 atm et 200 °R

 

1 u

 0.0123

4. Utiliser les figures médaillons (Carr) pour estimer

  N

2

 0.00042

  CO

2

 0.00026

  H S  0.00005 2

5. Déterminer la viscosité corrigée du gaz à pression atmospherique température du système

 1  0.0123  0.00042  0.00025  0.00005  0.01303 6. Déterminer

TPr 

660  1.80 366.53

PPr 

3500  5.07 690.61

7. A l’aide de la correlation graphique du rapport des viscosités de Carr estimer

g  1.52 1 Finalement, déterminer la viscosité du mélange gazeux

g   1

g

   1  1.52 x 0.01303  0.01981  

65

Exercice Calculer la viscosité d’un gaz naturel de densité 0.702 à 195 ° F et 1815 psia

66

Solution 1. Estimer les propriétés pseudo critiques à l’aide de la densité  g 2. Chercher les propriétés réduites PR = (1815 / 669) = 2.72

;

TR = (195 + 460) / 390 = 1.68

3. Lire à partir des figures ci-dessus

g  1.28 1  1  0.012 Finalement

g g    1 

   1  1.28 x 0.012  0.0154   67

Exercice Déterminer le facteur de compressibilité du mélange gazeux acide ci dessous, à 2000 psia et 150 °F.

a. Sans correction due aux CNH b. Avec correction due aux CNH Que concluez vous? Expliquer.

Composant N2 CO2 H2S Méthane Ethane Pr opane i  bu tan e n  bu tan e i  pen tan e n  pen tan e n  hexane n  hep tan e n  oc tan e n  nonane n  décane

fraction molaire 0.0345 0.0130 0.0000 0.8470 0.0586 0.0220 0.0035 0.0058 0.0027 0.0025 0.0028 0.0028 0.0015 0.0018 0.0015 68

Solution Sans correction MWa  19.91 ;  m 

19.91  0.686 29

PPC  663.3 psia

TPC  374.1  R

PPr 

2000  3.02 663.3

TTr 

(150  460) 610   1.63 374.1 374.1

Z  0.83 Avec correction Trouver le factor d ' ajustement de la T   120( A 0.9  A1.6 )  15( B 0.5  B 4.0 )



120 0.0130  0.0000

0. 9



 0.0130  0.0000 1. 6  0  2.29  R

TPC'  TPC    374.1  2.29  371.81  R PPC' 

PPC TPC' 663.3 x 371.81   659.24 psia TPC  B(1  B) 374.1  0

PPr 

2000  3.03 659.24

Donc , Z  0.84

TPr 

150  460  1.64 371.81

69

Standing a proposé une autre méthode mathématique pour estimer la viscosité à pression atmosphérique et température du système :

 1   1 u   CO   H S   N 2

 

1 u

2

2

 [1.709 x105  2.062 x106  g ] ( T  460 )  8.188 x103  6.15 x103 log  g

   

T = température du système en °R

1 u

  N

2

 CO



 y N 2 8.48 x10  3 log (  g )  9.59 x10  3

 8.49 x10

3 3  y 9 . 08 x 10 log (  )  6 . 24 x 10 CO2 g 2

  H S  y H S 2

2

3



 

log (  g )  3.73 x10  3

Lee, Gonzalez, et Eakin ont proposé une expression semi empirique en termes de température du système et Mwa pour estimer la viscosité du gaz

  g  Y     g  10 K exp  X  62 . 4     4

 g : en lb / ft à P et T du système 3

T : température du système MWa : MW apparent du mélange gazeux

X  3.5  K 



,

986  0.01 MWa T

9.4  0.02 MWa  T 1. 5 209  19 MWa  T

Y  2.4  0.2 X

70

Dean et Stiel ont proposé une autre méthode mathématique pour estimer la viscosité du gaz naturel à pression atmosphérique et température du réservoir. 8/9   T  1  34 x 10  5 Pr

for TPr 1.5

m

1  m

166.8 x10  5 ( 0.1338 TPr  0.0932) 5 / 9

m

for TPr  1.5

Est une paramètre de viscosité défini comme suit:

1/ 6 TPC  m  5.4402 2/3 MWa0. 5 PPC

Ils ont aussi préconisé

 g  1  r 





10.8 x10 5 exp  1.439  r   exp  1.111 r1.888

0.27 PPr Z TPr



m

 g : en à P et T du système 1 : en à 1 atm et T du système 71  r : masse volumique réduite du gaz

Viscosité de différents gaz à 1 atm

72

Densité

D e n s i t é

D e n s i t é

Viscosité de gaz d’hydrocarbures

73

Conductivité Thermique  dT  q  k    dx 

Flux de chaleur du à la conduction

[ BTU / hr ft 2 ]

La conductivité thermique, pour des mélanges de gaz naturels à pression élevée, peut être estimée à partir d'une valeur atmosphérique et d'une correction de pression.

Example Déterminer la conductivité thermique d’un gaz naturel de MW = 25 à 700 psia et 300 °F.

Solution 1. Chercher les propriétés critiques

TC  440 R

PC  660 psia

2. Calculer les propriétés réduites

Tr 

(300  460) 1.73 440

700 Pr   1.06 660 74

3. A l’aide de la figure ci-dessous déterminer la conductivité thermique kA à 1 atm

Conductivité thermique de gaz naturels et d'hydrocarbures at 1atm

k A  0.0248 Btu /[( hr . ft 2 .F ) / ft] or 0.0248 Btu . hr  1. ft  1.F  1

75

4. Déterminer le rapport

k  1.15 kA 5. Finalement, déterminer la k du gaz

k  k    k A  1.15 x 0.0248  0.0285 Btu hr  1 ft  1 F  1  kA 

MELANGES Méthode de Stiel et Thodos : Lire, à partir des diagrammes, k de chaque composant à la T désirée. km est estimée à l’aide de la Règle Racine Cubique applicable aux mélanges se composant de gaz simples et pas de CO2.

km

 yk    y i

i

i 3

3

MWi

MWi





Rapport de conductivité thermiques de gaz 76

Rapport de conductivité thermique

k kA

77

Exercice 12.1 A l’aide de la méthode Stiel-Thodos, chercher la conductivité thermique du mélange gazeux à 200 °F et 1 atm.

Composant

yi

N2

0.05

CH 4

0.80

C2 H 6

0.15

78

Propriétés Thermodynamiques - Enthalpie • gaz parfaits • gaz réels

- Entropie - Chaleur spécifique

79

Correlation Enthalpique Définition

H  U  PV

dH  dU  d (PV ) Forme différentielle U, P, et V sont des fonctions d’états

H  U  (PV ) H : fonction d’état

-Apparait fréquement dans les écoulements -Le changement de l’enthalpie avec T et P est complexe -La procédure de prédiction de ΔH de substances pures ou de mélanges est basée uniquement sur des données expérimentales, donc, les diagrammes P- H sont très recommandés et utilisés.

80

Effet de pression sur l’enthalpie d’écoulement de gaz naturels

Gaz Réels L’enthalpie de mélanges de gaz réels et des liquides peut être estimée à l’aide de calculs manuels. Ceux recommandés pour l'usage sont basés sur une extension du principe des états correspondants et sont donnés dans les figures ci-dessous.

La correlation applicable aux mélanges gazeux et liquides se compose de deux parties: Changement d’enthalpie avec la pression pour un fluide simple (fluide avec facteur acentrique zéro),

Correction pour la déviation d'un fluide réel par rapport au changement enthalpique avec la pression d'un fluide idéal.

Effet de pression sur l’enthalpie (fluide Simple)

81

Effet de pression sur l’enthalpie (Correction pour fluides réels)

Enthalpies d’états idéaux (parfaits) Les enthalpies de beaucoup de substances gazeuzes pures sont aisément corrélées en série de puissance de la température. Les figures ci-dessous montrent des valeurs typiques d’enthalpie de composants de gaz naturel.

82

Enthalpie idéale (correspondant à l’état idéal) de composants purs

Mélanges La référence d’enthalpie choisie est l’enthalpie zéro à pression et température absolues nulles, c’est la même référence utilisée dans API Project 44.1. Le choix de la référence est arbitraire et représente un moyen de convenance. La valeur absolue de l’enthalpie ne présente pas d’intérêt ; seules, ses variations entre deux états sont recherchées, puisqu’elles fournissent la quantité de chaleur à fournir ou à extraire. Les différences d’enthalpie qui sont les valeurs d’intérêt, ne sont pas altérées par le choix de la référence. Cependant, la même enthalpie de référence doit être utilisée pour tous les composants dans tous les calculs. La variation d'enthalpie de mélanges de gaz réels est calculé à l'aide d'une corrélation préparée à partir de mesures expérimentales d'enthalpie d'une variété de mélanges.



 

H TP  H 00  H T0  H 00  H T0  H TP

H TP



BTU / lb  mole

: l’enthalpie à pression et température d’intérêt

H

0 T

 H 00

 : l’enthalpie idéale au dessus de la référence H

H

0 T

 H TP

de l’enthalpie avec la pression, donné par la différence d’enthalpie entre l’enthalpie idéale  :etChangement l’enthalpie à la pression désirée; les deux quantitée sont à la température.

0

, à la température d’intérêt

H 00  0 à la référence choisie, température absolute zéro ou



HH  H H 0

0



H : enthalpie à T d ' int érêt 0

H : enthalpie idéale



HTP  HT0  HT0  HTP 83



Méthode de Calcul

H

0

H



calculée à partir de





0 (') 0 0       H  H H  H   0 H  H  R TC         R T R T C C       



H

0

 H / R TC

H

0

 H / R TC









0

( ')



Variation d’enthalpie avec la pression d’un fluide simple (donné par fig. cidessus) Correction due à la déviation d'un fluide réel par rapport à la variation de l'enthalpie idéale avec la pression, donnée par les figures ci-dessus.

Pour pouvoir utiliser les figures de gaz réels ci-dessus : - La composition du mélange doit être connue - Les pseudo T et P critiques du mélange sont calculées à l’aide de la règle de Kay - L’enthalpie moyenne du mélange

H m0   yi Hi0 H i0   enthalpie idéale de composant pur i  x MWi  84

Enthalpie de formation de différents gaz

85

Exemple Calculer l’enthalpie du mélange gazeux à 1010 psia et 120 °F.

Composant

yi

Méthane CO2

0.9010 0.0106

Ethane

0.0449

Pr opane i  Bu tan e

0.0187 0.0065

n  Bu tan e i  Pen tan e

0.0045 0.0017

n  Pen tan e Hexane

0.0019 0.0052

86

Solution. yi

MWi

TC  R 

PC  psia 

i

Méthane CO2

0.9010 0.0106

16.04 44.01

343.0 547.5

667.8 1071.0

0.0108 0.2667

292 100

Ethane

0.0449

30.07

549.8

707.8

0.0972

189

Pr opane i  Bu tan e n  Bu tan e

0.0187 0.0065 0.0045

44.10 58.12 58.12

665.7 734.6 765.3

616.3 529.1 550.7

0.1515 0.1852 0.1981

162 151 162

i  Pen tan e n  Pen tan e

0.0017 0.0019

72.15 72.15

828.7 845.3

490.4 488.6

0.2286 0.2510

151 158

Hexane

0.0052

86.18

912.0

470.0

0.2990

139

Composant

H i0 BTU / lb 

 m  0.0243

H 0  4857.31 BTU / lb  mole

H i0  enthalpie idéale du composant i ( figure : ideal enthalpy of pure components)

87

1. Déterminer les pseudo température et pression critiques du mélange

PPC  666.47 psia

TPC  367.96 R

Présence de CNH (CO2 ), donc correction des pseudo paramètres critiques (c< 5% donc on peut ignorer la correction)

  120 (0.01060.9  0.01061.6 )  1.92

TPC'  367.96  1.92  366.04  R PPC' 

666.47 x 366.04  662.99 psia 367.96

2. Déterminer les paramètres réduits

PPr 

1010  1.52 662.99

TPr 

(120  460)  1.59 366.04 88

3. Calculer





0

 H0  H     0.68 R T C  





 H0  H    R T C  

( ')

 0.015

et

  0.0243





0 ( ') 0 0       H  H H  H   0 H  H m  R TC         R T R T C C         1.987 x 366.04 x 0.68  (0.0243 x 0.015)  494.87 BTU / lb  mole 





4. Finalement, l’enthalpie du mélange est égale à l’enthalpie idéale moins l’enthalpie correspondant à la déviation par rapport à l’état idéal

H 0  H m  494.87 BTU / lb  mole  H m  H 0  494.87 H m  4857.31  494.87  4362.44 BTU / lb  mole 89

Correlation d’Entropie - Dépend des états initial et final, donc fonction d’état. - D’un point de vue microscopique: une augmentation d’entropie est associée à une augmentation de désordre (ou réduction d ‘ordre) au niveau moléculaire. - L'entropie est plus employée comme guide pour interpréter le comportement des gaz et des liquides dans les procédés de compression et d'expansion - Le changement de l'entropie de n'importe quel système subissant un processus réversible est égal à

dS 

dQR T

or

S 



dQR T

dQ : var iation d ' energie int erne L’entropie d’un mélange à multicomposants peut être évaluée en combinant l’entropie idéale (correspondant à l’état idéal) de API 44 avec les valeurs de variation de l’entropie avec la pression données par les tables de Curl et Pitzer. Il n’existe pas d’équations d’entropie pour les mélanges indéfinis (pseudo composants) mais, pour la plus part des cas où les pseudo composants sont présents en petite concentration, ils peuvent être approximés d'une manière satisfaisante par la paraffine hydrocarbonnée ayant le poids moléculaire le plus proche. 90

Méthode de calcul Similaire à celle de la correlation d’enthalpie 1. Calculer l’entropie idéale pour une phase fluide (gaz ou liquide) à une température donnée

Sm0   yi Si 0  R  yi ln yi

S i 0 : entropie idéale de i donnée par la figure

91

Entropie idéale de composants purs

2. L’effet de la pression (pour une T donnée) est calculée à l’aide dela correlation de Pitzer:

S

0

S



m

  S 0  S 0     R     R 

S0 S   R  

( ')

  Ln P [atm] 

S 0 S    R 

0

S 0 S    R 

( ')

92

Effet de pression sur l’entropie pour un fluide simple

Effet de pression sur l’entropie (Correction pour fluide réel)

Example Calculer l’entropie du mélange gazeux 1010 psia et 120 °F, (exemple précédent) yi

MWi

TC  R 

PC  psia 

i

Methane CO2

0.9010 0.0106

16.04 44.01

343.0 547.5

667.8 1071.0

0.0108 0.2667

3.150 1.176

Ethane

0.0449

30.07

549.8

707.8

0.0972

2.036

Pr opana i  Bu tan e n  Bu tan e

0.0187 0.0065 0.0045

44.10 58.12 58.12

665.7 734.6 765.3

616.3 529.1 550.7

0.1515 0.1852 0.1981

1.624 1.400 1.338

i  Pen tan e n  Pen tan e

0.0017 0.0019

72.15 72.15

828.7 845.3

490.4 488.6

0.2286 0.2510

1.260 1.245

Hexane

0.0052

86.18

912.0

470.0

0.2990

1.198

Component

 m  0.0243

S i 0 BTU / lb  R 

S 0  51.9016 BTU / lb  mole  R

S i0  Entropie idéale de i ( figure ideal entropy of pure components) 93

1. Determiner les pseudo temperature et pression critiques du mélange

PPC  666.47 psia

TPC  367.96 R

Presence de NHCs (CO2 ), donc correction (c< 5% donc on peut ignorer la correction)

  120 (0.0106 0.9  0.01061.6 )  1.92R

TPC'  367.96  1.92  366.04  R PPC' 

666.47 x 366.04  662.99 psia 367.96

2. Déterminer les paramètres réduits

PPr 

1010  1.52 662.99

TPr 

(120  460)  1.59 366.04 94

3. A l’aide des deux dernières figures









 S0  S     R 

0

 S0  S     0.345 R  

( ')

 0.065

4. Facteur acentrique apparent du mélange

  0.0243 5. Déterminer la différence d’entropie entre les états idéal et reel

S

0

S



m

( ')   S 0  S 0  S 0 S       Ln P   R     R    R    1010   1.987 0.345  0.0243 0.065  ln    14.7    9.093 BTU / lb  mole  R

6. Trouver l’entropie idéale pour le mélange

Sm0   yi Si 0  R  yi ln yi

(Note the Napierian logarithm)

S m0  51.9016  ( 0.920)  52.8216 BTU / lb  mole  R 7. Finalement, l’entropie du mélange est égale à l’entropie idéale moins l’entropie correspondant à la déviation de l’état idéal , ou bien utiliser l’équation



S m at P , T  S m0  S 0  S



m

 S m  52.8216  9.093

 43.7286 BTU / lb  mole R

95

Chaleur Spécifique Quantité de chaleur nécessaire pour augmenter la température de un degré d’une masse donnée d’un matériau.

dQ  n C dT

or

Chaleur spécifique molaire

dQ  m C dT Chaleur spécifique massique, Chaleur Spécifique

Définie pour seulement deux chemins différents : pression constante et volume constant :



mesurée à pression constante

CV

mesurée à volume constant

96

- Substance Homogène : Chaleur spécifique = f ( P,T ) -Chaleurs spécifiques idéales sont de bonnes approximations pour les chaleurs -spécifiques de gaz réels à faibles pressions. -Chaleurs spécifiques idéales sont fonction de la température seulement -(indépendentes de la pression)

'     T   T 2

(A) ( ' ) : idéal

'  a  b T  c T

C C R ' P

' V

2

(B)

Connaissant la dépendence de la température de l’une on trouvera celle de l’autre

97

Relation - CV

 dH  dU  R dT  dU  CV dT at cst V   C P  CV  R dH  C p dT at cst P 

98

Equation (A)

BTU /lb  mole F 

or

 cal /g  mole C

Constants for the molar heat capacity equation of organic gases in the ideal gas state

99

Equation (B)

BTU /lb  mole F 

or

 cal /g  mole C

Constants for the molar heat capacity equationof inorganic gases in the ideal gas state

100

Frequently asked to evaluate T

' ' C dT  C P mean T  T0   P T0

T

' C  P dT

C P' mean 

T0

T

 T0 

The base temperature is taken at a constant value such as 25°C and mean is determined as a function of the upper limit of integration .

' mean

is on next figures

e.g. : for CO2 : 12.1 BTU/lb-mole °F read at 2000 °F is the mean value between 77 and 2000 °F.

Gas Mixtures

C P' , m 

 i

yi C P' , i 101

Mean molar heat capacities of gases in the ideal gas state

Base temperature = 77 °F

102

Mean molar heat capacities of gases in the ideal gas state

Base temperature = 77 °F

103

104

Specific heat of hydrocarbon gases

Specific heat of hydrocarbon liquids

105

Exercise 15.1 Write the methane equation given below in of the following temperature units: a. °C, b. °R, c. °F. The molar heat capacity of methane in the zero-pressure state is given by the equation

'  3.381  18.044 x10 3 T  4.300 x10 6 T 2 Hint : T ( K ) = T( °R ) / 1.8 T ( K ) = [T( °F ) + 460] / 1.8 T ( K ) = T ( °C ) + 273

Answer a. C P'  7.99  15.70 x 10  3 T  4.300 x 10  6 T 2 b . C P'  3.381  10.03 x 10 3 T  1.327 x 10 6 T 2 c . C P'  7.79  8.81 x 10 3 T  1.327 x 10 6 T 2

106

Mid Term Exam Ex. 01 a. Expliquer brièvement et clairement ce qu’un point critique d’un gaz. b. When can it be said that two systems are in corresponding states. Explain using an example. c. Expliquer brièvement l’importance du facteur acentrique par rapport au principe des états correspondants..

Ex.02 Calculate the density of the following gas mixture at 1000 psia and 120 °F

Component

yi

CO2

0.10

H2S

0.15

C1

0.63

C2

0.02

C3

0.05

C4

0.05

Ex.03 Use the equations given below to calculate the heat required in to raise the temperature of ethane from 500 to 1000 °F in a flow process at a pressure of approximately 1 atm.

Q  H 

T2

' C  P dT T1

107

Mid Term Exam Correction Ex.01 Component CO2 H 2S C1 C2 C3 n  C4

yi

MWi

yi MWi

TCi  R 

yi TC i

PC i  psia 

yi PC i

0.10 0.15

44.01 34.08

4.401 5.112

547.91 672.45

54.791 100.868

1071 1300

107.100 195.000

0.63 16.043 0.02 30.07

10.107 0.601

343.33 549.92

216.298 10.998

666.4 706.5

419.832 14.130

0.05 44.097 0.05 58.123

2.205 666.06 33.303 2.906 765.62 38.281 MWa  25.336 TPC  454.539  R

616.0 550.6 PPC

30.800 27.530  794.392 psia

B  yH 2 S  0.15 A  yH 2 S  yCO2  0.15  0.1  0.25 1. Adjustment factor

  120 ( A0.9  A1.6 )  15 ( B 0.5  B 4.0 )   120 ( 0.250.9  0.251.6 )  15 ( 0.150.5  0.15 4.0 )  27.205 R 2. Corrected pseudo critical properties TPC'  454.539  27.205  427.334 R ' PC

P



TPC

PPC TPC' 794.392 x 427.334   741.190 psia  B (1  B )  454.539  0.15 (1  0.15 ) x 27.205

108

3. Reduced properties

PPr 

(120  460) 1000  1.349 ; TPr   1.357 741.190 427.334

4. Find compressibility factor fro Standing-Katz chart

Z  0.81 5. Finally calculate the density

g 

P MWa 1000 x 25.336   5.026 lb / ft 3 Z RT 0.81 x10.73 x (120  460)

with

psia . ft 3 R  10.73 lb  mole.R

109

Ex.02

ETHANE C P'  2.247  38.201 x10  3 T  11.049 x10  6 T 2

T  K

The required heat to raise temperature from T1 to T2

Q  H 

T2

' C  P dT T1

Q  H 

T2



(2.247  38.201 x 10 3 T 11.049 x 10 6 T 2 ) dT

T1

811

2 3  3 T 6 T  Q  H  2.247 T  38.201 x 10 11.049 x 10  2 3   533

Q  H  6354.35 cal /  g  mole  110