Ch6 Ans 361l6s
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 2z6p3t
Overview 5o1f4z
& View Ch6 Ans as PDF for free.
More details 6z3438
- Words: 30,832
- Pages: 96
Name
Class
Date
Additional Vocabulary
6-1
Roots and Radical Expressions
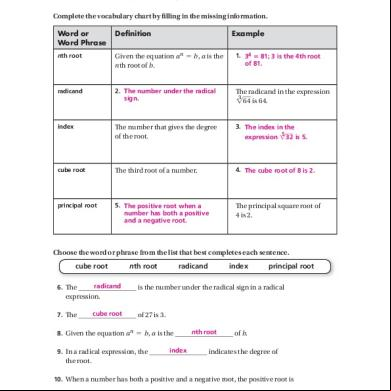
Complete the vocabulary chart by filling in the missing information. Word or Word Phrase
Definition
Example
nth root
Given the equation an 5 b, a is the nth root of b.
1. 34 5 81; 3 is the 4th root of 81.
radicand
2. The number under the radical sign.
The radicand in the expression 3 ! 64 is 64.
index
The number that gives the degree of the root.
3. The index in the
cube root
The third root of a number.
4. The cube root of 8 is 2.
principal root
5. The positive root when a number has both a positive and a negative root.
The principal square root of 4 is 2.
5
expression !32 is 5.
Choose the word or phrase from the list that best completes each sentence. cube root 6. The
nth root
radicand
radicand
index
principal root
is the number under the radical sign in a radical
expression. 7. The
cube root
of 27 is 3.
8. Given the equation an 5 b, a is the 9. In a radical expression, the
nth root
index
of b.
indicates the degree of
the root. 10. When a number has both a positive and a negative root, the positive root is
considered the
principal root
.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
1
Name
6-1
Class
Date
Think About a Plan Roots and Radical Expressions
Boat Building Boat builders share an old rule of thumb for sailboats. The maximum speed K in knots is 1.35 times the square root of the length L in feet of the boat’s waterline. a. A customer is planning to order a sailboat with a maximum speed of 12 knots. How long should the waterline be? b. How much longer would the waterline have to be to achieve a maximum speed of 15 knots? 1. Write an equation to relate the maximum speed K in knots to the length L in feet of a boat’s waterline. K 5 1.35!L
2. How can you find the length of a sailboat’s waterline if you know its maximum
speed? Substitute the maximum speed for K and solve the resulting equation for L
.
3. A customer is planning to order a sailboat with a maximum speed of 12 knots. How long should the waterline be? about 79 ft
4. How can you find how much longer the waterline would have to be to achieve
a maximum speed of 15 knots, compared to a maximum speed of 12 knots? Subtract the waterline length needed for a 12-knot maximum speed from the waterline length needed for a 15-knot maximum speed
5. If a customer wants a sailboat with a maximum speed of 15 knots, how long should the waterline be? about 123 ft
6. How much longer would the waterline have to be to achieve a maximum speed of 15 knots? about 44 ft
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
2
.
Name
Class
Date
Practice
6-1
Form G
Roots and Radical Expressions
Find all the real square roots of each number. 1. 400 220, 20
2. 2196 no real 3. 10,000 2100, 100 square roots
4. 0.0625 20.25, 0.25
Find all the real cube roots of each number. 5. 216 6
6. 2343 27
1000 8. 27 10 3
7. 20.064 20.4
Find all the real fourth roots of each number. 9. 281 no real fourth roots
12. 625 25, 5
10. 256 24, 4
11. 0.0001 20.1, 0.1
14. 2!25 25
15. !20.01 not a real 16. !0.001 0.1 number
Find each real root. 13. !144 12 4
17. !0.0081 0.3
3
3
3
18. !27 3
19. !227 23
20. !0.09 0.3
Simplify each radical expression. Use absolute value symbols when needed. 21. "81x4 9x2
22. "121y10 11 »y5…
3
5
3
23. " 8g6 2g2
3
24. " 125x9 5x3
25. " 243x5y15 3xy3
26. " (x 2 9)3
27. "25(x 1 2)4 5(x 1 2)2
3 3 64x9 28. %343 4x7
29. !20.008
31. "36x2y6 6»x…y3
4 32. " (m 2 n)4 »m 2 n…
4 x4
30. % 81
»x… 3
3
x29
20.2
33. A cube has volume V 5 s3 , where s is the length of a side. Find the side length for a cube with volume 8000 cm3. 20 cm
34. The temperature T in degrees Celsius (8C) of a liquid t minutes after heating is given by the formula T 5 8 !t . When is the temperature 488C? 36 min
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
3
Name
6-1
Class
Date
Practice (continued)
Form G
Roots and Radical Expressions
Find the two real solutions of each equation. 35. x2 5 4 22, 2
36. x4 5 81 23, 3
37. x2 5 0.16 20.4, 0.4
4 4 16 38. x2 5 49 27, 7
2 2 16 39. x4 5 625 25, 5
121 11 11 40. x2 5 625 225, 25
41. x2 5 0.000009 20.003, 0.003
42. x4 5 0.0001 20.1, 0.1
43. The number of new customers n that visit a dry cleaning shop in one year
is directly related to the amount a (in dollars) spent on advertising. This relationship is represented by n3 5 13,824a. To attract 480 new customers, how much should the owners spend on advertising during the year? $8000 44. Geometry The volume V of a sphere with radius r is given by the formula
V 5 43 pr3 . a. What is the radius of a sphere with volume 36p cubic inches? 3 in. b. If the volume increases by a factor of 8, what is the new radius? 6 in.
45. A clothing manufacturer finds the number of defective blouses d is a function
of the total number of blouses n produced at her factory. This function is d 5 0.000005n2 . a. What is the total number of blouses produced if 45 are defective? 3000 b. If the number of defective blouses increases by a factor of 9, how does the total number of blouses change? It has tripled. 46. The velocity of a falling object can be found using the formula v2 5 64h,
where v is the velocity (in feet per second) and h is the distance the object has already fallen. a. What is the velocity of the object after a 10-foot fall? about 25.30 ft/sec b. How much does the velocity increase if the object falls 20 feet rather than 10 feet? about 10.48 ft/sec
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
4
Name
6-1
Class
Date
Practice
Form K
Roots and Radical Expressions
Find all the real square roots of each number. 1. 625 625
2. 21.44 no real roots
16 3. 81 6 49
Find all the real cube roots of each number. 1 5. 64
4. 2216 26
6. 0.027 0.3
1 4
Find all the real fourth roots of each number. 7. 0.2401 60.7
8. 1 61
9. 21296 no real fourth roots
Find each real root. To start, find a number whose square, cube, or fourth is equal to the radicand. 4
10. !400
3
12. !2729 29
11. 2!256 24
5 "(20)2 20
Simplify each radical expression. Use absolute value symbols when needed. To start, write the factors of the radicand as perfect squares, cubes, or fourths. 3
13. "25x6
5 "(5)2(x3)2 5»x 3…
14. " 343x9y12 7x 3y 4
4
15. " 16x16y20 2x 4»y 5…
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
5
Name
6-1
Class
Date
Practice (continued)
Form K
Roots and Radical Expressions
4 16. The formula for the volume of a sphere is V 5 3 pr3 . Solving for r, the radius of 3 3V a sphere is r 5 Å 4p . If the volume of a sphere is 20 ft3, what is the radius of the sphere to the nearest hundredth? 1.68 ft
Find the two real solutions of each equation. 17. x4 5 81 63
2401 19. x4 5 625 w 75
18. x2 5 144 6 12
20. Writing Explain how you know whether or not to include the absolute value
symbol on your root. If the index is odd, then you do not use the absolute value symbol on your root. If the index is even, then you need the absolute value symbol on those variable with an odd power. 3
3
6
21. Arrange the numbers !264, 2!264, !64, and !64, in order from least to 3 3 6 , !64, 2 !264 , !64 greatest. !264
22. Open-Ended Write a radical that has no real values. Answers may vary. Sample: any even index radical with a negative radicand
23. Reasoning There are no real nth roots of a number b. What can you conclude
about the index n and the number b? The index n is even and the number b is negative.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
6
Name
Class
6-1
Date
Standardized Test Prep Roots and Radical Expressions
Multiple Choice For Exercises 1−6, choose the correct letter. 1. What is the real square root of 0.0064? B
0.4
0.04
0.08
no real square root
2. What is the real cube root of 264? G
4
28
24
no real cube root
16 3. What is the real fourth root of 281 ? D 2 3
249
223
no real fourth root 3
4. What is the value of !20.027? F
20.3
0.3
20.03
0.03
5. What is the simplified form of the expression "4x2y4 ? B
2xy2
2 u x uy2
4xy2
2 u xy u
6. What are the real solutions of the equation x4 5 81? H
29, 9
3
23, 3
23
Short Response 7. The volume V of a cube with side length s is V 5 s3. A cubical storage bin has
volume 5832 cubic inches. What is the length of the side of the cube? Show your work. 3
[2] V 5 s3, 5832 5 s3, s 5 !5832 5 18; 18 in. [1] incorrect side length OR no work shown [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
7
Name
Class
6-1
Date
Enrichment Roots and Radical Expressions
Rounding Roots and Radicals Computers treat radicals such as !2 as if they were rounded to a preassigned number of decimal places. Most computers round numbers according to an algorithm that uses the largest integer less than or equal to a given number. This function is called the greatest integer function and is written as y 5 fxg. As you can see, the graph of the greatest integer function is not continuous. The open circles indicate that the endpoint is not included as part of the graph. The command INT in most popular spreadsheet programs serves the same purpose as the greatest integer function. For instance, INT(3.84) 5 3; INT(21.99) 5 22; INT(7) 5 7. To round a number x to r decimal places, a computer performs the following procedure: y
Step 1
Multiply x by 10r.
Step 2
Add 0.5 to the result.
Step 3
Find INT of the result.
Step 4
Multiply the result by 102r.
2 x ⫺2
O
2
Fill in the table below to see how this procedure works. x
r
Step 1
Step 2
Step 3
Step 4
11.4825
3
11482.5
11483
11483
11.483
132.718
2
13271.8
13272.3
13272
132.72
34.999
1
349.99
350.49
350
35.0
A computer that rounds numbers after each operation may introduce rounding errors into calculations. To see the effects of rounding errors, perform each of the following computations for x 5 2 and different r values. First find the given root and write the answer to r 1 1 digits after the decimal. Carry out the four steps to get the answer and then raise the result to the given power. Write the answer again to r 1 1 digits after the decimal and carry out the four steps to get the final answer. 2
3
Q !x R
3
x
r
Q !x R
2
6
2.000001
2.000000
2
3
1.999
2.000
2
1
2.0
2.2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
8
Name
Class
6-1
Date
Reteaching Roots and Radical Expressions
For any real numbers a and b and any positive integer n, if a raised to the nth power equals b, then a is an nth root of b. Use the radical sign to write a root. The following expressions are equivalent: index
power an 5 b
g
radicand n
!b ! b5a
radical sign Problem
What are the real-number roots of each radical expression? 3
a. !343
b.
4 1 Å625
3
Because (7)3 5 343, 7 is a third (cube) root of 343. 3 Therefore, !343 5 7. (Notice that (27)3 5 2343, so 27 is not a cube root of 343.)
1 1 1 Because Q 15 R 4 5 625 and Q 215 R 4 5 625 , both 15 and 215 are real-number fourth roots of 625 .
c. !20.064
Because (20.4)3 5 20.064,20.4 is a cube root of 20.064 and is, in fact, the only one. 3 So, !20.064 5 20.4.
d. !225
Because (5)2 5 (25)2 5 25, neither 5 nor 25 are second (square) roots of 225. There are no real-number square roots of 225.
Exercises Find the real-number roots of each radical expression. 3
1. !169 213, 13 4. 7.
3
4
2. !729 9
218 212
5.
4 225 no real sq root
8. !0.1296 20.6, 0.6
Å
Å
4
10. !20.0001 no real 4th root
4
3. !0.0016 20.2, 0.2
Å121
2 2 211 , 11
4
11.
5 1 1 Å 243 3
6.
3 125 5 Å 216 6
3
9. !20.343 20.7 12.
3 8 Å 125
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
9
2 5
Name
Class
6-1
Date
Reteaching (continued) Roots and Radical Expressions n
You cannot assume that "an 5 a. For example, "(26)2 5 !36 5 6, not 26. This leads to the following property for any real number a: n
If n is odd
"an 5 a
If n is even
"an 5 u a u
n
Problem
What is the simplified form of each radical expression? 3
a. " 1000x3y9 3 3 " 1000x3y9 5 " 103x3(y3)3
Write each factor as a cube.
3 5" (10xy3)3
Write as the cube of a product.
5 10xy3
Simplify.
8
256g b. 4 4 16 Åh k
4
256g8
Å h4k16
5
4
44(g2)4
Å h4(k4)4
Write each factor as a power of 4.
2 4
4g 5 4 a 4b Å hk 5
4g2 u hu k4
Write as the fourth power of a quotient. Simplify.
The absolute value symbols are needed to ensure the root is positive when h is negative. Note that 4g2 and k4 are never negative.
Exercises Simplify each radical expression. Use absolute value symbols when needed. 3
13. "36x2 6»x… 16.
"x20 "y8
14. " 216y3 6y (x 1 3)3 17. 3 Å (x 2 4)6
x10 y4
27z3 19. 3 Å (z 1 12)6 (y 2 4)8 22. 4 Å (z 1 9)4
3z (z 1 12)2 (y 2 4)2 »z 1 9…
15. x 1 3 (x 2 4)2
4 20. " 2401x12 7»x3… 6 6
a b 23. 3 3 Å c
a 2b 2 c
1 Å 100x2
5 18. " x10y15z5 x2y3z
1331 21. 3 Å x3
11 x
3 24. " 2x3y6 2xy2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
10
1 10»x…
Name
Class
Date
Additional Vocabulary
6-2
Multiplying and Dividing Radical Expressions
Combining Radicals: Products n
n
n
n
n
If !a and !b are real numbers, then !a ? !b 5 !ab. Sample
3 3 3 3 !8 ? !27 5 !8 ? 27 5 !216 5 6
Solve. 3
3
1. !16 ? !4 5
3
3
!16 ? 4 5 !64 5 4
2. Which of the following products can be simplified? Circle the correct answer. 3 ! 12 ? !6
4 4 ! 16 ? ! 24
4 3 ! 35 ? ! 10
3
3. Write the radical expression !32x 4 in simplest form.
3 2x !4x
4. Which of the following products cannot be simplified? Circle the correct answer. 4 4 ! 15 ? ! 4
4 3 ! 10 ? ! 5
!4 ? !12
5. "4x2y3 ? "27x2y2 5
6x2y2"3y
Combining Radicals: Quotients n
n
n
If !a and !b are real numbers and b 2 0, then Sample
!8 5 !2
8 Å2
!a a 5 nÅb . n !b
5 !4 5 2
Solve. 6. Which of the following quotients can be simplified? Circle the correct answer. 3
3
!12
4
!6
3 !4
!20 3 !15
"3
"64x4 l4xl in simplest form. "4x2 8. Rewriting an expression so that there are no radicals in any denominator and no rationalizing the denominator denominators in any radical is called . 7. Write the radical expression
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
11
Name
6-2
Class
Date
Think About a Plan Multiplying and Dividing Radical Expressions
Satellites The circular velocity v, in miles per hour of a satellite orbiting Earth is 12
given by the formula v 5 Å1.24 3r 10 , where r is the distance in miles from the satellite to the center of the Earth. How much greater is the velocity of a satellite orbiting at an altitude of 100 mi than the velocity of a satellite orbiting at an altitude of 200 mi? (The radius of the Earth is 3950 mi.) Know
z
z
mi . 1. The first satellite orbits at an altitude of 100
z
z
mi . 2. The second satellite orbits at an altitude of 200
z
z
mi . 3. The distance from the surface of the Earth to its center is 3950
Need 4. To solve the problem I need to find: the difference in the velocities of a satellite orbiting at an altitude of 100 mi and one orbiting at an altitude of 200 mi
Plan 5. Rewrite the formula for the circular velocity of a satellite using a for the
altitude of the satellite. v 5 1.24 3 1012 Å a 1 3950 6. Use your formula to find the velocity of a satellite orbiting at an altitude of 100 mi. about 17,498 mi/h 7. Use your formula to find the velocity of a satellite orbiting at an altitude of 200 mi. about 17,286 mi/h 8. How much greater is the velocity of a satellite orbiting at an altitude of 100 mi than one orbiting at an altitude of 200 mi? about 212 mi/h
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
12
.
Name
Class
Date
Practice
6-2
Form G
Multiplying and Dividing Radical Expressions
Multiply, if possible. Then simplify. 1. !4 ? !25 10 3
3
4. " 45 ? " 75 15
3
2. !81 ? !36 54
3. !3 ? !27 9
5. !18 ? !50 30
6. !216 ? !4 24
3
3
Simplify. Assume that all variables are positive. 7. "36x3 6x !x
3 3 8. " 125y2z4 5z"y2z
3
3
10. " 216a12 22a4 !2 3
3 13. " 216x4y3 6xy "x
9. "18k6 3k3"2 4
4
11. "x2y10z xy5"z
12. " 256s7t12 4st3 "s3
14. "75r3 5r"3r
4 4 15. " 625u5v8 5uv2 !u
Multiply and simplify. Assume that all variables are positive. 3
16. !4 ? !6 2 "6
2 17. "9x2 ? "9y5 9xy !y
3 3 2 2 18. " 50x2z5 ? " 15y3z 5yz "6x
19. 4 !2x ? 3 !8x 48x
20. !xy ? !4xy 2xy
21. 9 !2 ? 3 !y 27 !2y
22. "12x2y ? " 3xy4
23. "29x2y4 ? " 12xy
24. 7"3y2 ? 2"6x3y
3
42xy"2xy
3
3
23xy "4y2
6xy2"xy
Divide and simplify. Assume that all variables are positive. 25.
"75 5 "3
26.
28.
"6x "2 "3x
29.
"(2x)2
2x 31. "(5y)4 25y2
"63xy3 "7y
3y !x
3
"4x2 3 "4x 3 "x 3
3 "18y2 " 12y 32. 3 2 "12y
27.
"54x5y3 3xy !3x "2x2y
3 4 243k 3 30. Ä 7
3k
162a
33. Ä 3 6a
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
13
k
3"3 a
Name
Class
6-2
Date
Practice (continued)
Form G
Multiplying and Dividing Radical Expressions
Rationalize the denominator of each expression. Assume that all variables are positive. 34.
!y "5y !5
35.
5
37.
9x 3"2x 2 2
38.
Å
"18x2y "2y3
41.
"4x2
!xy "3y !3x 3
4
!2x 4 "54x3 40. 4 "3x2 3x
3
"7xy2
36. 3
3x y
3 2 2 3 x2 " 9x y 39. Ä 3y 3y
x "2xy
Å8y
3
"14x2y2 2x
3 3a 42. Ä 2
3
"6abc2 4b c 2bc
4y
43. What is the area of a rectangle with length !175 in. and width !63 in.? 105 in.2 44. The area of a rectangle is 30 m2. If the length is !75 m, what is the width? 2"3 m
1 45. The volume of a right circular cone is V 5 3pr2h, where r is the radius of the base and h is the height of the cone. Solve the formula for r. Rationalize the denominator. r 5 "3πhV πh 4 46. The volume of a sphere of radius r isV 5 3pr3 . 3 3 "6π2V a. Use the formula to find r in of V. Rationalize the denominator. r 5 "3V; r 5 2π 4π b. Use your answer to part (a) to find the radius of a sphere with volume 100 cubic inches. Round to the nearest hundredth. 2.88 in.
Simplify each expression. Rationalize all denominators. Assume that all variables are positive. 47. !14 ? !21 7"6 50.
6 !2x 2"6x 5 5 !3
3
3
3
48. !150 ? !20 10 "3
8 3 4 "4x 2 x "2x
51. 3
49. !3 Q !12 2 !6 R 6 2 3"2 3
5 !xy4 3 2 52. 3 "5y "25xy2
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
14
Name
Class
Date
Practice
6-2
Form K
Multiplying and Dividing Radical Expressions
Multiply, if possible. Then simplify. To start, identify the index of each radical. 3
3
1. !4 ? !6
index of both radicals is 3
3
2. !5 ? !8 2 !10
4
3. !6 ? !9 The indexes are different, so you cannot multiply.
3 !4 ? 6 2 !3 3
Simplify. Assume all variables are positive. To start, change the radicand to factors with the necessary exponent. 3
4. " 27x6 3 3 5" 3 ? (x2)3 3x 2
5
5. "48x3y4 4xy 2 !3x
6. " 128x2y25 5
2y 5 "4x 2
Multiply and simplify. Assume all variables are positive. 4
4
3
8. " 7x6 ? " 32x2
7. !12 ? !3 6
3
9. 2" 6x4y ? 3" 9x5y2
4
3 18x 3y !2
2x 2 !14
Simplify each expression. Assume all variables are positive. 3
3
3 10. !4 ? !80 4 !5
11. 5"2xy6 ? 2"2x3y 20x 2y 3 !y
12. !5 Q !5 1 !15 R 5 1 5 !3
3
13. Error Analysis Your classmate simplified "5x3 ? " 5xy2 to 5x2y. What mistake did she make? What is the correct answer? She thought the indexes were the same. They are different, so you cannot multiply the radicands.
3 3 14. A square rug has sides measuring ! 16 ft by ! 16 ft. What is the area of the rug? 3 2 4 !4 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
15
Name
Class
6-2
Date
Practice (continued)
Form K
Multiplying and Dividing Radical Expressions
Divide and simplify. Assume all variables are positive. To start, write the quotient of roots as a root of a quotient. 15.
4
"36x6 "9x4
16.
"405x8y2 4
"5x3y2
3
17.
4
6 5 Å36x4 2x
3
"25x4 3
3x !x
9x
"75x7y2 x "3y 2
Rationalize the denominator of each quotient. Assume all variables are positive. To start, multiply the numerator and denominator by the appropriate radical expression to eliminate the radical. 3 "7x4y !26 ! x 18.
19. 3 !2
!3
5
20.
!26 !3 !78 ? !3 !3 3
!5xy
x !35x 5
3
!4x 2
21. Einstein’s famous formula E 5 mc2 relates energy E, mass m, and the speed of
light c. Solve the formula for c. Rationalize the denominator. !Em
E c 5 Åm ;c5 m
22. The formula h 5 16t2 is used to measure the time t it takes for an object to free fall from
height h. If an object falls from a height of h 5 18a5 ft, how long did it take for the object 2 to fall in of a? 3a !2a seconds 4
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
16
Name
Class
6-2
Date
Standardized Test Prep Multiplying and Dividing Radical Expressions
Multiple Choice For Exercises 1−5, choose the correct letter. Assume that all variables are positive. 3 3 1. What is the simplest form of ! 249x ? " 7x2 ?
7x !7x
B
27x
7x
3 2 27" x
4"5x7y6
4x3y3 !5x
3 15xy! y
5xy !15x
5x !x 2y
5x2y 2
2. What is the simplest form of "80x7y6 ? I
2x3y3 !20x
4x6y6"5x3 3
3
3. What is the simplest form of " 25xy2 ? " 15x2 ? A 3 5x" 3y2
3 5x ! 3y
4. What is the simplest form of
5"3x4 2"3y2
"75x5 ? G "12xy2
5x2 2y 3
2"x2y 5. What is the simplest form of 3 ? C "4xy2 3
"x2y 2y
3
3
"2xy2 y
x !2y y
3
!2y xy
Short Response 6. The volume V of a wooden beam is V 5 ls2, where l is the length of the beam
and s is the length of one side of its square cross section. If the volume of the beam is 1200 in.3 and its length is 96 in., what is the side length? Show your work. [2] V 5 ls2; s 5 ÅVl 5 Å1200 96 5 !12.5 N 3.5 in. [1] appropriate methods but with computational errors OR correct answer without work shown [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
17
Name
6-2
Class
Date
Enrichment Multiplying and Dividing Radical Expressions n
To simplify the radical !a, you look for a perfect nth power among the factors of the radicand a. When this factor is not obvious, it is helpful to factor the number into primes. Prime numbers are important in many aspects of mathematics. Several mathematicians throughout history have unsuccessfully tried to find a pattern that would generate the nth prime number. Other mathematicians have offered conjectures about primes that remain unresolved. 1. Goldbach’s Conjecture states that every even number n . 2 can be written as
the sum of two primes. For example, 4 5 2 1 2 and 10 5 3 1 7. Choose three even numbers larger than 50 and write them as a sum of two primes. Answers may vary. Sample: 52 5 47 1 5. 2. The Odd Goldbach’s Conjecture states that every odd number n . 5 can be
written as the sum of three primes. For example, 7 5 2 1 2 1 3. Choose three odd numbers larger than 50 and write them as the sum of three primes. Answers may vary. Sample: 51 5 37 1 11 1 3. 3. Another interesting pattern emerges when you examine a subset of the prime
numbers. Make a list of the primes less than 50. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 4. Make this list smaller by eliminating 2 and all primes that are 1 less than a
multiple of 4. 5, 13, 17, 29, 37, 41 5. The remaining primes in the list above are related in an interesting way. You
can write each prime as the sum of two squares. Express each of these primes as a sum of two squares. 5 5 1 1 4, 13 5 4 1 9, 17 5 1 1 16, 29 5 4 1 25, 37 5 1 1 36, 41 5 16 1 25 6. A Cullen number, named after an Irish mathematician James Cullen, is a
natural number of the form n 3 2n 1 1. Determine the first four Cullen numbers. That is, let n 5 1, 2, 3, 4. 3, 9, 25, 65 7. What is the smallest Cullen number that is a prime number? (The next Cullen
number that is a prime occurs when n 5 141!) 3 when n 5 1 8. A palindrome is a number that reads the same forward and backward. For
example, 121 is a palindromic number. List the seven palindromic primes that are less than 140. 2, 3, 5, 7, 11, 101, 131
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
18
Name
Class
6-2
Date
Reteaching Multiplying and Dividing Radical Expressions
You can simplify a radical if the radicand has a factor that is a perfect nth power and n is the index of the radical. For example: n
n
!xynz 5 y !xz Problem
What is the simplest form of each product? 3 3 a. ! 12 ? ! 10 n
n n Use !a ? !b 5 !ab.
3 3 3 ! 12 ? ! 10 5 ! 12 ? 10 3 5 "22 ? 3 ? 2 ? 5
Write as a product of factors.
3 3 5" 2 ?3?5
Find perfect third powers.
3 3 5 "23 ? "3 ? 5
n Use !ab 5 !a ? !b.
3 5 2! 15
Use "an 5 a to simplify.
n
n
n
b. "7xy3 ? "21xy2 n n n Use !a ? !b 5 !ab.
"7xy3 ? "21xy2 5 "7xy3 ? 21xy2 5 "7xy2y ? 3 ? 7xy2
Write as a product of factors.
5 "72x2(y2)2 ? 3y
Find perfect second powers.
5 7xy2"3y
Use !an 5 a to simplify.
n
Exercises Simplify each product. 3
3
1. !15x ? !35x 5x"21
2. " 50y2 ? " 20y 10y
4. 5"7x3y ? "28y2
5. 2" 9x5y2 ? " 2x2y5
70xy"xy
3
3
3 2x2y2 !18xy
3
6. !3 Q !12 2 !21 R 6 2 3"7
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
19
3
3
3. " 36x2y5 ? " 26x2y 26xy2 !x
Name
Class
Date
Reteaching (continued)
6-2
Multiplying and Dividing Radical Expressions
Rationalizing the denominator means that you are rewriting the expression so that no radicals appear in the denominator and there are no fractions inside the radical. Problem
What is the simplest form of
!9y !2x
?
Rationalize the denominator and simplify. Assume that all variables are positive. !9y !2x
5
9y Å 2x
Rewrite as a square root of a fraction.
5
9y ? 2x Å 2x ? 2x
Make the denominator a perfect square.
5
18xy Å 4x2
Simplify.
5
!18xy
Write the denominator as a product of perfect squares.
"22 ? x2
5
"18xy 2x
Simplify the denominator.
5
"32 ? 2 ? x ? y 2x
Simplify the numerator.
5
3"2xy 2x
Use !an 5 a to simplify.
n
Exercises Rationalize the denominator of each expression. Assume that all variables are positive. 3
"6ab2 8. 3 "2a4b
!5 "5x 7. x !x 3
11.
4"k9 3
16"k5
3
k "k 4
12.
4
4 "9y " 9x3y 9. 4 x "x
3
"3b a
4
"10 13. 4 "z2
3x5 x2"15xy Ä 5y 5y
4
"10z2 z
10.
3 19a2b " 19ac2 14. 3 4 c2 Ä abc
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
20
"10xy3 "30xy 6 "12y2
Name
6-3
Class
Date
Additional Vocabulary Binomial Radical Expressions
The column on the left shows the steps used to rationalize a denominator. Use the column on the left to answer each question in the column on the right. Problem
1. What does it mean to rationalize a
Rationalizing the Denominator
Write the expression
4 !3 !7 1 !3
denominator? Sample answer: It means to write
with a
an expression so that there are no
rationalized denominator.
radicals in any denominators and no denominators in any radicals. Multiply the numerator and the denominator by the conjugate of the denominator. 4 !3 !7 2 !3 ? !7 1 !3 !7 2 !3
2. What are conjugates? Conjugates are expressions that differ only in the signs of the first or second .
The radicals in the denominator cancel out. 4 !3A !7 2 !3B 723
3. Write and solve an equation to show
why the radicals in the denominator cancel out. (!7 1 !3)(!7 2 !3) 5 (!7 ? !7) 2 (!7 ? !3) 1 (!7 ? !3) 2 (!3 ? !3) 5 7 2 3
Distribute !3 in the numerator. 4( !3 ? !7 2 !3 ? !3) 723
4. What property allows you to distribute
Simplify. 4( !21 2 3) 4
5. Why do the fours in the numerator
the !3? The Distributive Property
and the denominator cancel out? Sample answer: Because 4 divided by 4 equals 1. 6. What number multiplied by !21
Simplify. !21 2 3
would produce a product of 21? !21
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
21
Name
Class
6-3
Date
Think About a Plan Binomial Radical Expressions
Geometry Show that the right triangle with legs of length !2 2 1 and !2 1 1 is similar to the right triangle with legs of length 6 2 !32 and 2. Understanding the Problem 1. What is the length of the shortest leg of the first triangle? Explain. !2 2 1 ; because !2 5 !2, !2 2 1 must be less than !2 1 1
2. What is the length of the shortest leg of the second triangle? Explain. 6 2 !32; because !32 is between 5 and 6, 6 2 !32 must be between 0 and 1, which is less than 2.
3. Which legs in the two triangles are corresponding legs? The smaller leg in the first triangle corresponds to the smaller leg in the second triangle. The larger leg in the first triangle corresponds to the larger leg in the second triangle.
Planning the Solution 4. Write a proportion that can be used to show that the two triangles are similar. !2 2 1 0 6 2 !32 !2 1 1
Getting an Answer 5. Simplify your proportion to show that the two triangles are similar. !2 2 1 !2 1 1
0 6 2 2!32
2(!2 2 1) 0 (!2 1 1)(6 2 !32) 2 !2 2 2 0 6 !2 2 !64 1 6 2 !32 2 !2 2 2 0 6 !2 2 8 1 6 2 4 !2 2 !2 2 2 5 2 !2 2 2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
22
2
Name
Class
Date
Practice
6-3
Form G
Binomial Radical Expressions
Add or subtract if possible. 1. 9 !3 1 2 !3
2. 5 !2 1 2 !3
11 !3
5 !2 1 2 !3
3
3
3
3
3 !7 2 7 !x
3
6. 5 !xy 1 !xy 3 6 !xy
3
9. 7 !x 1 x !7
4. 14 !xy 2 3 !xy 3 11 !xy
5. 8 !x 1 2 !y 3 3 8 !x 1 2 !y
7. !3x 2 2 !3x
8. 6 !2 2 5 !2 3
6 !2 2 5 !2
2!3x
3
3. 3 !7 2 7!x
3
3
7 !x 1 x !7
Simplify. 10. 3 !32 1 2 !50 22 !2 4
4
13. 2 !48 1 3 !243 4
13 !3
3
3
3
12. !81 2 3 !3 0
14. 3 !75 1 2 !12 19 !3
15. !250 2 !54
4
16. !28 2 !63 2!7
3
11. !200 2 !72 4 !2
4
3
2 !2
17. 3 !32 2 2 !162 0
18. !125 2 2 !20 !5
20. A1 1 4 !10B A2 2 !10B
21. A1 2 3 !7B A4 2 3 !7B
Multiply. 19. A1 2 !5B A2 2 !5B
238 1 7"10
7 2 3 !5 22. (4 2 2 !3)2
23. (!2 1 !7)2
24. A2 !3 2 3 !2B 2
9 1 2 !14
30 2 12 !6
28 2 16 !3 25. A4 2 !3B A2 1 !3B 5 1 2 !3
67 2 15 !7
26. A3 1 !11B A4 2 !11B 1 1 !11
27. A3 !2 2 2 !3B 2 30 2 12 !6
Multiply each pair of conjugates. 28. (3 !2 2 9)(3 !2 1 9) 263
29. (1 2 !7)(1 1 !7) 26
30. (5 !3 1 !2)(5 !3 2 !2) 73
31. (3 !2 2 2 !3)(3 !2 1 2 !3) 6
32. (!11 1 5)(!11 2 5) 214
33. (2 !7 1 3 !3)(2 !7 2 3 !3) 1
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
23
Name
Class
6-3
Date
Practice (continued)
Form G
Binomial Radical Expressions
Rationalize each denominator. Simplify the answer. 34.
3 2 !10 !5 2 2 !2 3 !5 2 !2
35.
3
2 1 !14 !2 !7 1 !2
36.
2 1 !x 3 !x
3
x 1 2 "x2 x
Simplify. Assume that all the variables are positive. 37. !28 1 4 !63 2 2 !7 12 !7
38. 6 !40 2 2 !90 2 3 !160 26 !10
39. 3 !12 1 7 !75 2 !54 41 !3 2 3 !6
3 3 40. 4 !81 1 2 !72 2 3 !24 6 !3 1 4 !9
41. 3 !225x 1 5 !144x 105 !x
42. 6"45y2 1 4"20y2 26y !5
43. A3 !y 2 !5B A2 !y 1 5 !5B 6y 1 13 !5y 2 25
44. A !x 2 !3B A !x 1 !3B
3
3
3
x23
300 ft
300 V3 ft
600 ft
sidewalk
45. A park in the shape of a triangle has a sidewalk dividing it into two parts.
300 V6 ft
300 V3 ft
a. If a man walks around the perimeter of the park, how far will he walk? (900 1 300 !3 1 300 !6) ft or about 2154 ft b. What is the area of the park? 270,000 1 90,000 !3 2
ft2 or about 212,942 ft2
46. The area of a rectangle is 10 in.2. The length is A2 1 !2B in. What is the width? 5(2 2 !2) in. 47. One solution to the equation x2 1 2x 2 2 5 0 is 21 1 !3. To show this,
let x 5 21 1 !3 and answer each of the following questions.
a. What is x2? 4 2 2 !3 b. What is 2x? 22 1 2 !3 c. Using your answers to parts (a) and (b), what is the sum x2 1 2x 2 2? 0
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
24
Name
6-3
Class
Date
Practice
Form K
Binomial Radical Expressions
Simplify if possible. To start, determine if the expressions contain like radicals. 3
1. 3 !5 1 4 !5
both radicals 7 !5
3
2. 8 !4 2 6 !4 3 2 !4
3. 2 !xy 1 2 !y no; cannot simplify
4. A floor tile is made up of smaller squares. Each square measures 3 in. on each side. Find the perimeter of the floor tile. 24 !2 in.
Simplify. To start, factor each radicand. 4
5. !18 1 !32
4
6. !324 2 !2500 4
22 !4 or 22 !2
5 !9 ? 2 1 !16 ? 2 7 !2
3
3
7. !192 1 !24 3
6 !3
Multiply. 8. A3 2 !6B A2 2 !6B 12 2 5 !6
9. A5 1 !5B A1 2 !5B 24 !5
10. A4 1 !7B 2 23 1 8"7
Multiply each pair of conjugates. 11. A7 2 !2B A7 1 !2B 47
12. A1 1 3 !3B A1 2 3 !3B 226
13. A6 1 4 !7B A6 2 4 !7B 276
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
25
Name
Class
6-3
Date
Practice (continued)
Form K
Binomial Radical Expressions
Rationalize each denominator. Simplify the answer. 14.
3 2 1 !6
5
15.
2 2 !6 3 ? 2 1 !6 2 2 !6
7 1 !5 6 2 !5
16.
47 1 13 !5 31
1 2 2 !10 4 1 !10 4 2 32 !10
23 1 32 !6
17. A section of mosaic tile wall has the design shown at the
right. The design is made up of equilateral triangles. Each side of the large triangle is 4 in. and each side of a small triangle is 2 in. Find the total area of the design to the nearest tenth of an inch. A N 17.3 in.2
Simplify. Assume that all variables are positive. 18. !45 2 !80 1 !245 6 !5
19. A2 2 !98B A3 1 !18B 236 2 15 !2
21. Error Analysis A classmate simplified the 1 using the steps shown. expression 1 2 !2
What mistake did your classmate make?
20. 6"192xy2 1 4"3xy2 52y !3x
1 2 !2 1 ? 1 2 !2 1 2 !2 1 2 !2
5 122 5
1 2 !2 5 21 1 !2 21
What is the correct answer? The student multiplied the denominator by itself instead of by its conjugate; 21 2 !2
22. Writing Explain the first step in simplifying !405 1 !80 2 !5. First, factor each radicand so you can combine like radicals.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
26
Name
Class
6-3
Date
Standardized Test Prep Binomial Radical Expressions
Multiple Choice For Exercises 1−5, choose the correct letter. 1. What is the simplest form of 2!72 2 3 !32? D
2 !72 2 3 !32
24 !2
22 !2
0
2. What is the simplest form of A2 2 !7B A1 1 2 !7B? F
212 1 3 !7
16 1 5 !7
212 2 3 !7
3 1 !7
3. What is the simplest form of A !2 1 !7B A !2 2 !7B? C
9 1 2 !14
9 2 2 !14
4. What is the simplest form of
214 1 7 !5
25
7 ? F 2 1 !5
9
214 2 7 !5
14 1 7 !5
14 2 7 !5 3
3
3
5. What is the simplest form of 8!5 2 !40 2 2 !135? D 3 16 ! 5
3 12 ! 5
3 4! 5
0
Short Response 6. A hiker drops a rock from the rim of the Grand Canyon. The distance it falls d
in feet after t seconds is given by the function d 5 16t2 . How far has the rock fallen after (3 1 !2) seconds? Show your work. [2] d 5 16t2 5 16(3 1 !2)2 5 16(11 1 6 !2) 5 176 1 96 !2 ft [1] appropriate method but with computational errors [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
27
Name
Class
6-3
Date
Enrichment Binomial Radical Expressions
Consider how you might use a calculator to find the square of negative three. If you enter the expression 232, your calculator produces an answer of 29. However, the square of negative three is (23)2 5 (23)(23) 5 9. Calculators follow the order of operations. Therefore, a calculator will compute 232 as the opposite of 32. The correct input is (23)2 , which is correctly evaluated as 9. Be sure to follow the order of operations when expanding binomial radical expressions. 1. Consider the algebraic expression (a 1 b)2 . Is (a 1 b)2 equivalent to a2 1 b2 ?
If yes, explain. If not, explain why it is not mathematically logical and give a counterexample. Answer may vary. Sample: (a 1 b)2 means (a 1 b)(a 1 b) which, when expanded, is a2 1 2ab 1 b2 , which is not equivalent to a2 1 b2 .
2. Are there values of a and b for which (a 1 b)2 5 a2 1 b2 ? Answers may vary. Sample: a 5 1, b 5 0
Consider each pair of expressions below for nonnegative values of the variables. State whether they are equivalent expressions. If yes, explain. If not, give a counterexample. 3. "x2 1 y2, "x2 1 "y2 Answers may vary. Sample: These expressions are not equivalent. Let x 5 2 and y 5 3 then "22 1 32 5 "13 u "4 1 "9 "a
a
4. b , Åb Answers may vary. Sample: These expressions are not equivalent. Let a = 6 and !6
b 5 2 then 2 N 1.22 and Å62 5 !3 N 1.73 5. Q !a R 2, a Answers may vary. Sample: These expressions are equivalent. A !aB 2 5 A !aB A !aB 5 "a2 5 a for all a L 0. 2
6. Q "x2 1 y2 R , x 1 y Answers may vary. Sample: These expressions are not equivalent. Q "x2 1 y2 R Q "x2 1 y2 R 5 "(x2 1 y2)2 5 x2 1 y2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
28
Name
Class
Date
Reteaching
6-3
Binomial Radical Expressions
Two radical expressions are like radicals if they have the same index and the same radicand. Compare radical expressions to the in a polynomial expression. Like :
4x3
11x3
Unlike :
4y3
11x3
Like radicals:
4!6
3
3 11 ! 6
Unlike radicals:
4!5
3
3 11 ! 6
The power and the variable are the same 4y2
Either the power or the variable are not the same. The index and the radicand are the same
2
4 "6
Either the index or the radicand are not the same.
When adding or subtracting radical expressions, simplify each radical so that you can find like radicals. Problem
What is the sum? !63 1 !28 !63 1 !28 5 !9 ? 7 1 !4 ? 7
Factor each radicand.
5 "3 2 ? 7 1 "2 2 ? 7
Find perfect squares.
5 "3 2 "7 1 "2 2 "7
n n n Use !ab 5 !a ? !b.
5 3 !7 1 2 !7
Use "an 5 a to simplify.
5 5 !7
Add like radicals.
n
The sum is 5!7.
Exercises Simplify. 1. !150 2 !24 3 !6 3
3
3
4. 5 !2 2 !54 2 !2
3
3
3
2. !135 1 !40 5 !5
3. 6 !3 2 !75 !3 3
3
3
5. 2!48 1 !147 2 !27 0 6. 8 !3x 2 !24x 1 !192x 3
10 !3x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
29
Name
Class
Date
Reteaching (continued)
6-3
Binomial Radical Expressions
• Conjugates, such as !a 1 !b and !a 2 !b, differ only in the sign of the second term. If a and b are rational numbers, then the product of conjugates produce a rational number: 2
2
Q !a 1 !b R Q !a 2 !b R 5 Q !a R 2 Q !b R 5 a 2 b.
• You can use the conjugate of a radical denominator to rationalize the denominator. Problem
What is the product? Q 2 !7 2 !5 R Q 2 !7 1 !5 R Q 2 !7 2 !5 R Q 2 !7 1 !5 R These are conjugates. 2
5 Q 2 !7 R 2 Q !5 R
2
Use the difference of squares formula.
5 28 2 5 5 23
Simplify.
Problem
How can you write the expression with a rationalized denominator?
4 !2 1 1 !3
4 !2 1 1 !3
5
4 !2 1 2 !3 ? 1 1 !3 1 2 !3
Use the conjugate of 1 1 !3 to rationalize the denominator.
5
4 !2 2 4 !6 123
Multiply.
5
A4 !2 2 4 !6B 4 !2 2 4 !6 5 2 22 2
Simplify.
5
24 !2 1 4 !6 5 22 !2 1 2 !6 2
Exercises Simplify. Rationalize all denominators. 7. A3 1 !6B A3 2 !6B 3 10.
2 2 !7 2 1 !7 211 1 4"7 3
8.
2 !3 1 1 "3 1 1 2 5 2 !3
11. A2 !8 2 6B A !8 2 4B 40 2 28 !2
9. Q 4 !6 2 1 R Q !6 1 4 R 12.
!5 2 1 !3 2 !5 2 !15
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
30
20 1 15 !6
Name
Class
Date
Additional Vocabulary
6-4
Rational Exponents
Choose the word or phrase from the list that best matches each sentence. rational exponent
radical form
4
1. The expression " y3 is written in rational exponent
2. A
exponential form
radical form
.
is an exponent written in fractional form.
3
3. The expression x 5 is written in
exponential form
.
Write each expression in exponential form. 7
4
4. " y7 5
y4 4
3
x3
5
a5
5. (!x)4 5
3
6. (!a)3 5 8
7. !r 5
1
r8
Write each expression in radical form. 3
4 " w3
8. w4 5 5
"b5
1
"h
9. b2 5 10. h2 5 3
7 3 11. g 7 5 "g
Multiple Choice 6 4 " y
12. What is 3 1
y2
!y
in simplest ? B 3 ! y
3 4 " y
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
31
2
y3
Name
Class
Date
Think About a Plan
6-4
Rational Exponents
Science A desktop world globe has a volume of about 1386 cubic inches. The radius of the Earth is approximately equal to the radius of the globe raised to the 10th power. Find the radius of the Earth. (Hint: Use the formula V 5 43pr3 for the volume of a sphere.) Know
z
z
1386 in.3 . 1. The volume of the globe is
2. The radius of the Earth is equal to the radius of the globe raised to the 10th power
.
Need 3. To solve the problem I need to find the radius of the Earth
Plan 4. Write an equation relating the radius of the globe rG to the radius of the
Earth rE. rE 5 rG 10
5. How can you represent the radius of the globe in of the radius of the
Earth? 1
rG 5 rE 10 6. Write an equation to represent the volume of the globe. 1386 5 43πrG3
7. Use your previous equation and your equation from Exercise 5 to write an
equation to find the radius of the Earth. 1
1386 5 43 π ¢ rE10 ≤
3
8. Solve your equation to find the radius of the Earth. about 251,000,000 in. or 3961 mi
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
32
.
Name
Class
Date
Practice
6-4
Form G
Rational Exponents
Simplify each expression. 1
1
1. 1253 5 1
1
2. 642 8
1
1
4. 72 ? 72 7 1
1
1
1
3. 325 2 1
1
5. (25)3 ? (25)3 ? (25)3 25 1
7. 113 ? 113 ? 113 11 10. 122 ? 272 18
1
1
8. 72 ? 282 14 1
1
1
1
1
1
6. 32 ? 752 15 9. 84 ? 324 4
1
11. 123 ? 453 ? 503 30
1
1
12. 182 ? 982 42
Write each expression in radical form. 4 3 13. x3 " x4
1 3 14. (2y)3 " 2y
15. a1.5 "a3
1 5 16. b5 !b
2 3 2 17. z3 " z
1 4 18. (ab)4 !ab
5 12 19. m2.4 " m
2 20. t27
21. a21.6
1 7 "t2
1 5 "a8
Write each expression in exponential form. 3
3
1
3
22. "x3 x 2
1
23. !m m3 1 2
24. !5y (5y)2 3
4
25. " 2y2 23y 3
26. Q !b R 3 b4
28. "(6a)4 36a2
29. " n4 n5
5
4
1
27. !26 (26)2 4
3
30. " (5ab)3 (5ab)4
31. The rate of inflation i that raises the cost of an item from the present value P to F 1t the future value F over t years is found using the formula i 5 Q P R 2 1. Round
your answers to the nearest tenth of a percent.
a. What is the rate of inflation for which a television set costing $1000 today will become one costing $1500 in 3 years? 14.5% b. What is the rate of inflation that will result in the price P doubling (that is, F 5 2P) in 10 years? 7.2%
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
33
Name
Class
Date
Practice (continued)
6-4
Form G
Rational Exponents
Write each expression in simplest form. Assume that all variables are positive. 1
1
32. Q 814 R 4 81
33. Q 325 R 5 32
35. 70 1
36. 83 4
1
1
34. A2564 B 4 256
2
5
1
2
37. (227)3 9 3
1
1
38. x2 ? x3 x 6
39. 2y2 ? y 2 y 2
40. A82 B 3 4
41. 3.60 1
1 1 42. Q 16 R 4 1 2
27 2 43. Q 8 R 3 9 4 1
8
44. " 0 0 1
45. 2
1
47. Q 3a2 b3 R 2 9ab3
50.
2 y5
?
1 1
59.
?
?
1 x3
3 x4
y6
1
b3
1
3
1
52. Q 2a4 R 3 8a4
2 x 21 13
1
1 2 55. Q 9x4y22 R 2 3x y
1 2
1
1 x6
3
1 4y2 2
1
2b x3
12y3
49. Q a3b22 R 26 a4
54. Q 2x5 R Q 6x4 R 12x 20
2 27x6 3 3x 56. a b 4 4 64y 4y 3 1 x4
x7
2
53. 8122 9
46.
1
2
51. a
y 40
7 12x 6
48. Q y3 R 29 y6 4
31
3 y8
1 2 Q 3x2 R Q 4x3 R
57.
x 2 y3 1 1 x 3 y2
1
5
1
1 x23 y 2 60. a 2 1 b x3 y22
1
1
58. y8 4 y2 y8
x6 y6 y3 x2
1
12x8 2 2x4 61. a b 5y5 75y10
62. In a test kitchen, researchers have measured the radius of a ball of dough
made with a new quick-acting yeast. Based on their data, the radius r of the t dough ball, in centimeters, is given by r 5 5(1.05)3 after t minutes. Round the answers to the following questions to the nearest tenth of a cm. a. What is the radius after 5 minutes? 5.4 cm b. What is the radius after 20 minutes? 6.9 cm c. What is the radius after 43 minutes? 10.1 cm
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
34
Name
Class
6-4
Date
Practice
Form K
Rational Exponents
Simplify each expression. 1
1. 16 4 4 ! 16 2
1
1
1
2. (23) 3 ? (23) 3 ? (23) 3 23
1
1
3. 5 2 ? 45 2 15
Write each expression in radical form. 1
4. x 4 4
!x
4
2
5. x 5
6. x 9
5
9
"x 4
"x 2
Write each expression in exponential form. 3
7. !2 1
23
3
3
8. " 2x2
9. " (2x)2
1
2
A2x 2 B 3
(2x) 3
10. Bone loss for astronauts may be prevented with an apparatus that rotates a0.5 , N is the rate of rotation in to simulate gravity. In the formula N 5 2pr 0.5
revolutions per second, a is the simulated acceleration in m/s2, and r is the radius of the apparatus in meters. How fast would an apparatus with the following radii have to rotate to simulate the acceleration of 9.8 m/s2 that is due to Earth’s gravity? a. r 5 1.7 m 0.382 rev/s b. r 5 3.6 m 0.263 rev/s c. r 5 5.2 m 0.218 rev/s d. Reasoning Would an apparatus with radius 0.8 m need to spin faster or slower than the one in part (a)? faster
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
35
Name
Class
Date
Practice (continued)
6-4
Form K
Rational Exponents
Simplify each number. 1
12. 2431.2 729
11. (2216) 3 3 ! 2216 26
13. 32 20.4 1 4
Find each product or quotient. To start, rewrite the expression using exponents. 4
5
3
14. A !6B A !6B 1
1
15. 12
7 5 Q 6 4 R Q 6 3 R "6
"x2 10
3
16. !20 ? !135
x2
%
6
6 "5 5
5
!x
Simplify each number. 2
2
17. (125) 3
2
18. (216) 3(216) 3
25
2
19. (2243) 5
1296
9
Write each expression in simplest form. Assume that all variables are positive. 3
20. Q 16x28 R 24 x6 8
1
x2 3 22. a 210 b x x4
1
21. Q 8x15 R 2 3 1 2x 5
23. Error Analysis Explain why the following
simplification is incorrect. What is the correct simplification? You cannot multiply 5 and 1
5 2 together by multiplying bases. You have to rewrite 5 as 51 and combine the exponents; 20 2 5 !5.
1
5Q4 2 5 2 R 1
1
5 5(4) 2 5 Q 5 2 R 5 20 2 25 2 5 15
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
36
Name
Class
Date
Standardized Test Prep
6-4
Rational Exponents
Multiple Choice For Exercises 1−5, choose the correct letter. 1
1
1
1. What is 123 ? 453 ? 503 in simplest form? B
!27,000 1
1
30
1073
27,000
3 " (xy)2
3 2 " xy
2
2. What is x3 ? y3 in simplest form? I
x3"y3 1
"xy3 1
1
3. What is x3 ? x2 ? x4 in simplest form? A 13
1
x 12
1
x 24
x 24
1
x
5 xy 2
y2
6
2 1
4. What is £
5
x9
x3y3
1 3≥
in simplest form? I
x2y4 5
5
x 7y 2
xy 2
5
1
5. What is (232x10 y35)25 in simplest form? C 2 2 2 7 x y
2x2y7
2
1 2x2 y7
2 x2 y7
Short Response 6. The surface area S, in square units, of a sphere with volume V, in cubic units, 1
2
is given by the formula S 5 p 3(6V )3 . What is the surface area of a sphere with volume 43 mi3? Show your work. 1
2
1
2 3
1
2
1
2
[2] S 5 π 3 (6V) 3 5 π 3 c 6 Q 43 R d 5 π 3 (8) 3 5 4π 3 mi
[1] appropriate method but some computational errors [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
37
Name
6-4
Class
Date
Enrichment Rational Exponents
Power Games Each problem below involves rational exponents. Some of the problems are tricky. Good luck! 1. Begin with any positive number. Call it x. Divide x by 2. Call the result r. Now
follow these directions carefully. You may use a calculator. final r 5 !x Divide x by r. Call the result q. Add q and r. Call the result s. Divide s by 2. Call the result r. Go back to step a. Repeat steps a–d until r no longer changes. What is the relationship between the original x and the final result?
a. b. c. d.
2. If we take the square root of a number 6 times, it would look like this:
'& $#" !x Rewrite the expression above using rational exponents.
1 1 1 1 1 1 2 2 2 2 2 a a a a ax2 b b b b b
Simplify the expression above. Express the denominator of the exponent as a 1 power of 2. x64 ; 26 If you were to take the square root of a number 10 times, what would the 10 12 denominator of the exponent be equal to if you use rational exponents? 12 times? 2 ; 2 Choose any number and repeatedly take the square root. What number is the answer approaching? 1 Does the answer appear to approach the same number if you change the number you choose? yes In Exercises 3–6, assume that the square roots and the operations inside them repeat forever. 3. How much is $2 3 #2 3 "2 3 !2 3 c? (Hint: Let
y 5 $2 3 #2 3 "2 3 !2 3 c. Then use substitution and solve the equation y 5 "2 3 y.) 2 4. How much is $2 1 #2 1 "2 1 !2 1 c? 2 5. How much is $2 2 #2 2 "2 2 !2 2 c? 1 3 6. How much is $2 4 #2 4 "2 4 !2 4 c? " 2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
38
Name
Class
Date
Reteaching
6-4
Rational Exponents
You can simplify a number with a rational exponent by converting the expression to a radical expression: 1
1 2 92 5 !9 53
n
xn 5 !x, for n . 0
1 3 83 5 ! 852
You can simplify the product of numbers with rational exponents m and n by raising the number to the sum of the exponents using the rule am ? an 5 am1n Problem
What is the simplified form of each expression? 1
1
1
1
a. 364 ? 364 1
1
364 ? 364 5 364 1 4
Use am ? an 5 am1n .
1
5 362
Add.
2 5 !36
Use xn 5 !x.
56
Simplify.
1
n
3
2
b. Write Q 6x3 R Q 2x4 R in simplified form. 3
2
Q 6x3 R Q 2x4 R
3
2
5 6 ? 2 ? x3 ? x4 2
Commutative and Associative Properties of Multiplication
3
5 6 ? 2 ? x3 1 4
Use xm ? xn 5 xm1n.
17
5 12x12
Simplify.
Exercises Simplify each expression. Assume that all variables are positive. 1
2
1
2 1
1
7
2. Q 2y4 R Q 3y3 R 6y 12
1. 53 ? 53 5 13
4. 2y3 y5 2y 15
1
1
1
1
5. 54 ? 54 !5
1
2
6. Q 23x 6 R Q 7x 6 R 221 !x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
39
1
3. (211)3 ? (211)3 ? (211)3 211
Name
Class
Date
Reteaching (continued)
6-4
Rational Exponents
To write an expression with rational exponents in simplest form, simplify all exponents and write every exponent as a positive number using the following rules for a 2 0 and rational numbers m and n: 1 a2n 5 n a
1 a2m
5 am
(am)n 5 amn
(ab)m 5 ambm
Problem 2
What is A8x9y23 B 23 in simplest form? 2
(8x9y23)23
2
5 A23 x9 y23 B 23 2
2
Factor any numerical coefficients. 2
5 A23 B 23 Ax9 B 23 Ay23 B 23
Use the property (ab)m 5 ambm.
5 222x26y2
Multiply exponents, using the property (am)n 5 amn.
y2 5 2 6 2 x y2 5 6 4x
Write every exponent as a positive number. Simplify.
Exercises Write each expression in simplest form. Assume that all variables are positive. 1
1
7. A16x2 y8 B 22 4xy4 1
10. A25x26 y2 B 2 5y x3
1
8. Az23 B 9
1
1 4
9. Q 2x4 R
1 z3
16z4 12. a b 25x8
2
11. A8a23 b9 B 3 4b6 a2
1
x2 5 2 1 13. a 21 b x 5y 5 y 3
16. A9z10 B 2 27z15
16x 1
22
1
2
14. A27m9 n23 B 23
1
17. (2243)25 21 3
n2 9m6
1
32r2 4 15. a 4 b 2r 2 2s s 2 x5 10 18. a 1 b y2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
40
5x4 4z2
x4 y5
Name
Class
6-5
Date
Additional Vocabulary Solving Square Root and Other Radical Equations
Problem 3 Solve the equation 4" (y 1 2)2 1 3 5 19. Justify your steps. Then check your solution. 2
4(y 1 2)3 1 3 5 19 2
4(y 1 2)3 5 16 2
(y 1 2)3 5 4 2 3
3 2
Subtract 3 from each side. Divide each side by 4.
3
c(y 1 2) d 5 42 (y 1 2) 5 8 y56 3 4" (6 1 2)2 1 3 0 19
Check
Rewrite the radical using a rational exponent.
3 2 4" 8 1 3 0 19
4 ? 4 1 3 0 19 19 5 19
3
Raise each side to the 2 power. Simplify. Solve for y. Substitute 6 for y. Add. Simplify the radical. Simplify.
Exercise Solve the equation 9"(2x 2 4)4 1 2 5 38. Justify your steps. Then check your solution. 4
9(2x 2 4)2 1 2 5 38 9(2x 2 4)2 5 36
1
c(2x 2 4)2 d 5 42 (2x 2 4) 5 2 x53 Check
Subtract 2 from each side and simplify the exponent. Divide each side by 9.
(2x 2 4)2 5 4 1 2
Rewrite the radical using a rational exponent.
9"(2 ? 3 2 4)4 1 2 0 38 9"16 1 2 0 38 38 5 38
Raise each side to the 12 power. Simplify. Solve for x. Substitute 3 for x. Simplify the expression under the radical sign. Simplify.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
41
Name
6-5
Class
Date
Think About a Plan Solving Square Root and Other Radical Equations
Traffic Signs A stop sign is a regular octagon, formed by cutting triangles off the corners of a square. If a stop sign measures 36 in. from top to bottom, what is the length of each side? Understanding the Problem x
1. How can you use the diagram at the right to find a
relationship between s and x? s
Since the triangles are right triangles, use the Pythagorean Theorem to relate s and x
.
36 in.
2. How can you use the diagram at the right to find another
x
s
x
relationship between s and x? The length of a side of the square, which is s 1 2x, is the same as the height of the stop sign from top to bottom
.
3. What is the problem asking you to determine? the length s of each side of the stop sign
Planning the Solution 4. What are two equations that relate s and x? 2x2 5 s2 ; 2x 1 s 5 36 5. How can you use your equations to find s? Solve the first equation for x and substitute the result into the second equation
.
Getting an Answer 6. Solve your equations for s. about 14.9 in. 7. Is your answer reasonable? Explain. Yes; the length of one side of the stop sign is a little more than a third of the total height of the sign
. Prentice Hall Algebra 2 • Teaching Resources
Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
42
Name
Class
Date
Practice
6-5
Form G
Solving Square Root and Other Radical Equations
Solve. 1. 5 !x 1 2 5 12 4
2. 3 !x 2 8 5 7 25
3. !4x 1 2 5 8 9
4. !2x 2 5 5 7 27
5. !3x 2 3 2 6 5 0 13
6. !5 2 2x 1 5 5 12 222
7. !3x 2 2 2 7 5 0 17
8. !4x 1 3 1 2 5 5 32
9. !33 2 3x 5 3 8
3
3
10. !2x 1 1 5 3 13
11. !13x 2 1 2 4 5 0 5
3
12. !2x 2 4 5 22 22
Solve. 1
1
13. (x 2 2) 3 5 5 127
14. (2x 1 1)3 5 23 214
1
1
16. 2x 3 2 2 5 0 1
17. x 2 2 5 5 0 25
1
1
19. (7x 2 3)2 5 5 4
20. 4x 2 2 5 5 27 64
1
2
22. (2x 1 1)3 5 1 0
3
15. 2x 4 5 16 16 3
18. 4x 2 2 5 5 103 9 1
21. x 6 2 2 5 0 64 4
23. (x 2 2)3 2 4 5 5 29, 225 24. 3x 3 1 5 5 53 8, 28
25. The formula P 5 4"A relates the perimeter P, in units, of a square to its area A, in square units. What is the area of the square window shown below? 36 ft2
Perimeter: 24 ft
2
26. The formula A 5 6V 3 relates the surface area A, in square units, of a cube to
the volume V, in cubic units. What is the volume of a cube with surface area 486 in.2? 729 in.3 27. A mound of sand at a rock-crushing plant is growing over time. The equation
3 t5 ! 5V 2 1 gives the time t, in hours, at which the mound has volume V, in cubic meters. When is the volume equal to 549 m3? 14 h
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
43
Name
Class
Date
Practice (continued)
6-5
Form G
Solving Square Root and Other Radical Equations
28. City officials conclude they should budget s million dollars for a new library
building if the population increases by p thousand people in a ten-year census. The 2 formula s 5 2 1 13(p 1 1)5 expresses the relationship between population and library budget for the city. How much can the population increase without the city going over budget if they have $5 million for a new library building? 242,000
Solve. Check for extraneous solutions. 29. !x 1 1 5 x 2 1 3
30. !2x 1 1 5 23 no solution
1
1
31. (x 1 7)2 5 x 2 5 9
32. (2x 2 4)2 5 x 2 2 2, 4
33. !x 1 2 5 x 2 18 23
34. !x 1 6 5 x 9
1
1
35. (2x 1 1)2 5 25 no solution
36. (x 1 2)2 5 10 2 x 7
37. !x 1 1 5 x 1 1 21, 0
38. !9 2 3x 5 3 2 x 0, 3
3
5
39. !2x 2 4 5 22 22
40. 2 !5x 1 2 2 1 5 3 6
41. !4x 1 2 5 !3x 1 4 2
42. !7x 2 6 2 !5x 1 2 5 0 4
1
1
1
1
43. 2(x 2 1)2 5 (26 1 x)2 10
44. (x 2 1)2 2 (2x 1 1)4 5 0 4
45. !2x 2 !x 1 1 5 1 8
46. !7x 2 1 5 !5x 1 5 3
1
1
1
1
47. (7 2 x)2 5 (2x 1 13)2 22
48. (x 2 7)2 5 (x 1 5)4 11
49. !x 1 9 2 !x 5 1 16
50. !8x 2 !6x 2 2 5 0 21
3
3
51. A clothing manufacturer uses the model a 5 !f 1 4 2 !36 2 f to estimate
the amount of fabric to order from a mill. In the formula, a is the number of apparel items (in hundreds) and f is the number of units of fabric needed. If 400 apparel items will be manufactured, how many units of fabric should be ordered? 32 52. What are the lengths of the sides of the trapezoid shown at the right if the
perimeter of the trapezoid is 17 cm?
x
x 5 4 cm, 2 !x 5 4 cm, x 1 1 5 5 cm 2 Vx
2 Vx x⫹1
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
44
Name
Class
Date
Practice
6-5
Form K
Solving Square Root and Other Radical Equations
Solve. To start, rewrite the equation to isolate the radical. 1. !x 1 2 2 2 5 0
2. !2x 1 3 2 7 5 0 23
!x 1 2 5 2 2
3. 2 1 !3x 2 2 5 6 6
Solve. 3
2
4. 2(x 2 2) 3 5 50
5. 2(x 1 3) 2 5 54 6
127 and 2123
1
6. (6x 2 5) 3 1 3 5 22 220
V
7. The formula d 5 2#ph relates the diameter d, in units, of a cylinder to its
volume V, in cubic units, and its height h, in units. A cylindrical can has a diameter of 3 in. and a height of 4 in. What is the volume of the can to the nearest cubic inch? 28 in.3
8. Writing Explain the difference between a radical equation and a polynomial equation. A radical equation has a variable in a radicand or a variable with a rational exponent, while a polynomial equation has a variable with whole number exponents.
3
9. Reasoning If you are solving 4(x 1 3) 4 5 7, do you need to use the absolute value to solve for x? Why or why not? No; the numerator of the exponent 34 is not even.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
45
Name
Class
Date
Practice (continued)
6-5
Form K
Solving Square Root and Other Radical Equations
Solve. Check for extraneous solutions. First, isolate a radical, then square each side of the equation. 10. !4x 1 5 5 x 1 2
A !4x 1 5B 2 5 (x 1 2)2
11. !23x 2 5 2 3 5 x 22
12. !x 1 7 1 5 5 x 9
1 and 21
13. !2x 2 7 5 !x 1 2
A !2x 2
7B 2
5 A !x 1
2B 2
14. !3x 1 2 2 !2x 1 7 5 0 15. !2x 1 4 2 2 5 !x 5 0 and 16
9
16. Find the solutions of !x 1 2 5 x. 2 a. Are there any extraneous solutions? 21 b. Reasoning How do you know the answer to part (a)? Substitute the solutions into the original equation. If a solution does not make the equation true, then the solution is extraneous.
17. A floor is made up of hexagon-shaped tiles. Each hexagon tile has
an area of 1497 cm2. What is the length of each side of the hexagon? (Hint: Six equilateral triangles make one hexagon.) about 24 cm s s!3 2
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
46
Name
Class
Date
Standardized Test Prep
6-5
Solving Square Root and Other Radical Equations
Gridded Response Solve each exercise and enter your answer in the grid provided. 1. What is the solution? !2x 2 4 2 3 5 1
1
2. What is the solution? 5x 2 2 8 5 7
3. What is the solution? !2x 2 6 5 3 2 x
4. What is the solution? !5x 2 3 5 !2x 1 3
5. Kepler’s Third Law of Orbital Motion states that the period P (in Earth years)
it takes a planet to complete one orbit of the sun is a function of the distance d (in astronomical units, AU) from the planet to the sun. This relationship is 3 P 5 d 2 . If it takes Neptune 165 years to orbit the sun, what is the distance (in AU) of Neptune from the sun? Round your answer to two decimal places.
Answers 1.
–
10 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
2. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
9 0 1 2 3 4 5 6 7 8 9
3. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
3 0 1 2 3 4 5 6 7 8 9
4. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
2 0 1 2 3 4 5 6 7 8 9
5. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
47
–
30 . 08 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Name
Class
Date
Enrichment
6-5
Solving Square Root and Other Radical Equations
When solving radical equations you will often get an extraneous solution. You can use a graph to explain why an algebraic answer is not a solution. 1. Solve the equation !x 1 2 5 x 2 4. Is there an extraneous solution? 7; 2 is an extraneous solution.
2. To analyze this equation with a graph, rewrite the equation as a system of two
equations. What two equations can you write? y 5 !x 1 2 and y 5 x 2 4
8 y 4 ᎐8 ᎐4 O ᎐4
3. Graph the two equations.
x 4
8
᎐8
4. Explain how you find the solution to this system of equations on your graph.
What is the solution?
Answers may vary. Sample: On a graph the solution to a system of equations is the point of intersection; the solution for this system is (7, 3).
5. How can you use the solution from the graph of the system of equations to
help you solve the original equation !x 1 2 5 x 2 4? Answers may vary. Sample: The x-coordinate of the solution to the system is the solution to the original equation. 6. How can you tell from your graph that one of your algebraic answers is an
extraneous solution? Answers may vary. Sample: Because there is only one point of intersection, there can only be one solution to the equation.
Solve each equation. Graph each equation as a system to determine if there are any extraneous solutions. 7. !4x 1 1 5 3
8. x 5 !6 2 x
8 y
8 y
4 ᎐8 ᎐4 O ᎐4
9. !x 1 1 5 x 2 1
4
8 y
4
x 8
⫺4 ⫺4
᎐8
4
8
⫺8
2; no extraneous solutions
4
x
⫺4 ⫺4
x 4
8
⫺8
2; 23 is an extraneous solution.
3; 0 is an extraneous solution.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
48
Name
Class
Date
Reteaching
6-5
Solving Square Root and Other Radical Equations
Equations containing radicals can be solved by isolating the radical on one side of the equation, and then raising both sides to the same power that would undo the radical. Problem
What is the solution of the radical equation? 2!2x 1 2 2 2 5 10 2 !2x 1 2 2 2 5 10 2 !2x 1 2 5 12
Add 2 to each side.
!2x 1 2 5 6
Divide each side by 2.
(!2x 1 2)2 5 62
Square each side to undo the radical.
2x 1 2 5 36
Simplify.
2x 5 34
Subtract 2 from each side.
x 5 17
Divide each side by 2.
Check the solution in the original equation. Check 2 !2x 1 2 2 2 5 10 2 !2(17) 1 2 2 2 0 10 2 !36 2 2 0 10
Write the original equation. Replace x by 17. Simplify.
12 2 2 0 10 10 5 10 The solution is 17.
Exercises Solve. Check your solutions. 1
2. 3 !2x 5 12 8
1. x 2 5 13 169 1
4. (3x 1 4)2 2 1 5 4 7 1
7. (x 1 2) 2 2 5 5 0 23
1
3. !3x 1 5 5 11 12
5. (6 2 x) 2 1 2 5 5 23
6. !3x 1 13 5 4 1
8. !3 2 2x 2 2 5 3 211
3 9. !5x 1 2 2 3 5 0 5
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
49
Name
Class
6-5
Date
Reteaching (continued) Solving Square Root and Other Radical Equations
An extraneous solution may satisfy equations in your work, but it does not make the original equation true. Always check possible solutions in the original equation. Problem
What is the solution? Check your results. !17 2 x 2 3 5 x !17 2 x 2 3 5 x !17 2 x 5 x 1 3
Add 3 to each side to get the radical alone on one side of the equal sign.
A !17 2 xB 2 5 (x 1 3)2
Square each side.
17 2 x 5 x2 1 6x 1 9 0 5 x2 1 7x 2 8
Rewrite in standard form.
0 5 (x 2 1)(x 1 8)
Factor.
x 2 1 5 0 or x 1 8 5 0 x 5 1 or
Set each factor equal to 0 using the Zero Product Property.
x 5 28
Check !17 2 x 2 3 5 x !17 2 1 2 3 0 1 !16 2 3 0 1 151
!17 2 x 2 3 5 x !17 2 (28) 2 3 0 28 !25 2 3 0 28 2 2 28
The only solution is 1.
Exercises Solve. Check for extraneous solutions. 10. !5x 1 1 5 !4x 1 3 2
11. !x2 1 3 5 x 1 1 no 12. !3x 5 !x 1 6 3 solution
13. x 5 !x 1 7 1 5 9
14. x 2 3 !x 2 4 5 0 16
15. !x 1 2 5 x 2 4 7
16. !2x 2 10 5 x 2 5 5, 7
17. !3x 2 6 5 2 2 x 2
18. !x 2 1 1 7 5 x 10
19. !5x 1 1 5 !3x 1 15 7 20. !x 1 9 5 x 1 7 25
21. x 2 !x 1 2 5 40 47
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
50
Name
Class
6-6
Date
Additional Vocabulary Function Operations
Darnell wrote the steps to compose the following functions on index cards, but the cards got mixed up. Let f (x) 5 x 1 7 and g(x) 5 x3. What is (g + f )(24)?
Subtract 4 from 7.
Substitute 24 for x in f(x).
Raise 3 to the 3rd power.
Substitute 3 into g(x).
Use the note cards to write the steps in order. 1. First, substitute 24 for x in f(x) . 2. Second, subtract 4 from 7 . 3. Then, substitute 3 into g(x) . 4. Finally, raise 3 to the 3rd power .
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
51
Name
6-6
Class
Date
Think About a Plan Function Operations
Sales A salesperson earns a 3% bonus on weekly sales over $5000. Consider the following functions. g(x) 5 0.03x
h(x) 5 x 2 5000
a. Explain what each function above represents. b. Which composition, (h + g)(x) or (g + h)(x), represents the weekly bonus?
Explain. 1. What does x represent in the function g(x)? the sales amount used to calculate a 3% bonus 2. What does the function g(x) represent? the bonus earned by the salesperson on sales 3. What does x represent in the function h(x)? the total weekly sales made by the salesperson 4. What does the function h(x) represent? the weekly sales over $5000 made by the salesperson 5. What is the meaning of (h + g)(x)? First multiply the value of x by 0.03, then subtract 5000 from the result
.
6. Assume that x is $7000. What is (h + g)(x)? −4790 7. What is the meaning of (g + h)(x)? First subtract 5000 from the value of x, then multiply the result by 0.03
.
8. Assume that x is $7000. What is (g + h)(x)? 60 9. Which composition represents the weekly bonus? Explain (g + h)(x) represents the weekly bonus because you must first find the sales amount over 5000 by subtracting 5000 from the weekly sales, and then you multiply the result by the bonus percent as a decimal, or 0.03
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
52
.
Name
6-6
Class
Date
Practice
Form G
Function Operations
Let f (x) 5 4x 21 and g(x) 5 2x2 1 3. Perform each function operation and then find the domain. 1. ( f 1 g)(x) 2x2 1 4x 1 2; all real numbers 4. ( f ? g) (x) 8x3 2 2x2 1 12x 23; all real numbers
2. ( f 2 g)(x) 22x2 + 4x 24; all real numbers f 5. g (x) 4x 2 1 ; 2x2 1 3
3. (g 2 f )(x) 2x2 2 4x 1 4; all real numbers g 6. (x) f
all real numbers
2x2 1 3 4x 2 1 ;
all real numbers except 14
Let f (x) 5 2x and g(x) 5 !x 21. Perform each function operation and then find the domain of the result. 7. ( f 1 g)(x)
8. ( f 2 g)(x)
9. (g 2 f )(x)
2x 2 "x 1 1; x L 0
2x 1 "x 2 1; x L 0
f 11. g (x)
10. ( f ? g)(x)
2x ; !x 2 1
2x"x 2 2x; x L 0
22x 1 "x 2 1; x L 0
g 12. (x) f x L 0 and x u 1
"x 2 1 2x ; x S 0
x
Let ƒ(x) 5 23x 1 2, g(x) 5 5 , h(x) 5 22x2 1 9, and j(x) 5 5 2 x. Find each value or expression. 13. ( f + j)(3) 24
14. ( j + h)(21) 22
15. (h + g)(25) 7
17. ƒ(x) 1 j(x) 24x 1 7
18. ƒ(x) 2 h(x) 2x2 2 3x 2 7
19. (g + f )(25) 5
20. ( f + g)(22) 16 5
21. 3ƒ(x) 1 5g(x) 28x 1 6
22. g( f (2)) 2 4 5
23. g( f (x)) 23x 1 2
24. f (g(1)) 7
16. (g + f )(a) 23a 1 2 5
17
5
5
25. A video game store adds a 25% markup on each of the games that it sells.
In addition to the manufacturer’s cost, the store also pays a $1.50 shipping charge on each game. a. Write a function to represent the price f (x) per video game after the store’s markup. f(x) 5 1.25x b. Write a function g(x) to represent the manufacturer’s cost plus the shipping charge. g(x) 5 x 1 1.5 c. Suppose the manufacturer’s cost for a video game is $13. Use a composite function to find the cost at the store if the markup is applied after the shipping charge is added. f(g(13)) N $18.13 d. Suppose the manufacturer’s cost for a video game is $13. Use a composite function to find the cost at the store if the markup is applied before the shipping charge is added. g(f(13)) 5 $17.75 Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
53
Name
Class
6-6
Date
Practice (continued)
Form G
Function Operations
4 26. The formula V 5 3 π r 3 expresses the relationship between the volume V and
radius r of a sphere. A weather balloon is being inflated so that the radius is changing with respect to time according to the equation r 5 t 1 1, where t is the time, in minutes, and r is the radius, in feet. a. Write a composite function f (t) to represent the volume of the weather balloon after t minutes. Do not expand the expression. f(t) 5 43 π(t 1 1)3 b. Find the volume of the balloon after 5 minutes. Round the answer to two decimal places. Use 3.14 for π. 904.32 ft3
27. A boutique prices merchandise by adding 80% to its cost. It later decreases by
25% the price of items that do not sell quickly. a. Write a function f (x) to represent the price after the 80% markup. f(x) 5 1.8x b. Write a function g(x) to represent the price after the 25% markdown. g(x) 5 0.75x c. Use a composition function to find the price of an item, after both price adjustments, that originally costs the boutique $150. g(f (150)) 5 $202.50 d. Does the order in which the adjustments are applied make a difference? Explain. No; it doesn’t matter whether you first multiply by 0.75 or by 1.8. 28. A department store has marked down its merchandise by 25%. It later
decreases by $5 the price of items that have not sold. a. Write a function f (x) to represent the price after the 25% markdown. f(x) 5 0.75x b. Write a function g(x) to represent the price after the $5 markdown. g(x) 5 x 2 5 c. Use a composition function to find the price of a $50 item after both price adjustments. g(f (50)) 5 $32.50 d. Does the order in which the adjustments are applied make a difference? Explain. Yes; multiplying by 0.75 and then subtracting by 5 is different than subtracting by 5 and then multiplying by 0.75.
Let g(x) 5 x2 2 5 and h(x) 5 3x 1 2. Perform each function operation. 29. (h + g)(x) 3x2 2 13
30. g(x) ? h(x) 3x3 1 2x2 2 15x 2 10
31. 22g(x) 1 h(x) 22x2 1 3x 1 12
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
54
Name
Class
6-6
Date
Practice
Form K
Function Operations
Let f (x) 5 4x 1 8 and g(x) 5 2x 2 12. Perform each function operation and then find the domain of the result. 1. ( f 1 g)(x)
(f ? g) (x)
(f 2 g) (x)
f (x) 1 g(x) (f 1 g) (x) 5 6x 2 4; all real numbers
f 4. a g b(x)
3. ( f ? g)(x)
2. ( f 2 g)(x)
f
5 2 32x 2 96; all real numbers
5 2x 1 20; all real numbers
2x 1 4
Q g R (x) 5 x 2 6 ;
8x2
all real numbers, xu6
Let f (x) 5 x 1 2 and g(x) 5 !x 2 1. Perform each function operation and then find the domain of the result. f 7. a g b(x)
6. ( f ? g)(x)
5. ( f 1 g)(x) (f 1 g)(x) 5 x 1 !x 1 1; all x L 0
g 8. a b(x) f
(f ? g)(x) f x 1 2 Q R (x) 5 ; !x 2 1 5 x !x 2 x 1 2 !x 2 2; g all x L 0, x u 1 all x L 0
g
all x L 0
Let f (x) 5 x 2 2 and g(x) 5 x2 . Find each value. To start, use the definition of composing functions to find a function rule. 9. (g f )(4)
°
10. ( f g)(21) 21
°
f (4) 5 4 2 2 5 2 4
11. (g f )(23)
°
25
Let f (x) 5 !x and g(x) 5 (x 1 2)2 . Find each value. 12. ( f g)(25)
°
3
13. ( f g)(0)
°
2
14. (g f )(4)
°
16
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
55
!x 2 1
Q f R (x) 5 x 1 2 ;
Name
Class
Date
Practice (continued)
6-6
Form K
Function Operations
15. A car dealer offers a 15% discount off the list price x of any car on the lot. At the same
time, the manufacturer offers a $1000 rebate for each purchase of a car. a. Write a function f (x) to represent the price after discount. f(x) 5 0.85x b. Write a function g (x) to represent the price after the $1000 rebate. g(x) 5 x 2 1000 c. Suppose the list price of a car is $18,000. Use a composite function to find the price of the car if the discount is applied before the rebate. $14,300 d. Suppose the list price of a car is $18,000. Use a composite function to find the price of the car if the discount is applied after the rebate. $14,450 e. Reasoning Between parts (c) and (d), will the dealer want to apply the discount before or after the rebate? Why? After; they will make more money selling the car for a higher price.
16. Error Analysis f (x) 5 2 !x and g(x) 5 3x 2 6. Your friend gives a domain f for a g b(x) as x $ 0. Is this correct? If not, what is the correct domain? No; the correct domain is x L 0, x u 2.
Let f (x) 5 2x2 2 3 and g(x) 5
x11 2 . Find each value.
17. f (g(2)) 3
18. g( f (23)) 8
2
19. ( f f )(21) 21
°
20. Reasoning A local bookstore has a sale on all their paperbacks giving a 10% discount.
You also received a coupon in the mail for $4 off your purchase. If you buy 2 paperbacks at $8 each, is it less expensive for you to apply the discount before the coupon or after the coupon? How much will you save? before the coupon; $.40
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
56
Name
Class
6-6
Date
Standardized Test Prep Function Operations
Multiple Choice For Exercises 125, choose the correct letter. 1. Let f (x) 5 22x 1 5 and g(x) 5 x3. What is (g 2 f )(x)? B
x3 2 2x 1 5
2x3 2 2x 1 5
x3 1 2x 2 5
2x3 1 2x 2 5
2. Let f (x) 5 3x and g(x) 5 x2 1 1. What is ( f · g)(x)? H
9x2 1 3x
9x2 1 1
3x3 1 3x
3x3 1 1 f
3. Let f (x) 5 x2 2 2x 2 15 and g(x) 5 x 1 3. What is the domain of g (x)? C
all real numbers
x 2 23
x 2 5, 23
x.0
4. Let f (x) 5 !x 1 1 and g(x) 5 2x 1 1. What is (g + f )(x)? F
2 !x 1 3
!2x 1 1 1 1
2x !x 1 2x 1 !x 1 1
2x 1 !x 1 2
1 5. Let f (x) 5 x and g(x) 5 x2 2 2. What is ( f + g)(23)? B 17 9
17
1 7
29
7
23
Short Response 6. Suppose the function f (x) 5 0.035x represents the number of U.S. dollars
equivalent to x Russian rubles and the function g(x) 5 90x represents the number of Japanese yen equivalent to x U.S. dollars. Write a composite function that represents the number of Japanese yen equivalent to x Russian rubles. Show your work. [2] (g ° f )(x) 5 g(f(x)) 5 90(0.035x) 5 3.15x [1] appropriate method but with one computational error [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
57
Name
6-6
Class
Date
Enrichment Function Operations
Composition and Linear Functions Two functions f (x) and g(x) are equal if they have the same domains and the same value for each point in their domain. Suppose that f (x) 5 Ax 1 B and g(x) 5 Cx 1 D are two linear functions both of whose domains are the set of real numbers. 1. If f (x) 5 g(x), what can you conclude by examining the values of f and g at x 5 0? B 5 D 2. Use your conclusion to eliminate D from the definition of g(x). g(x) 5 Cx 1 B 3. What equation results from examining the values of f and g at x 5 1? A 1 B 5 C 1 B 4. What can you conclude about A and C? A 5 C 5. When are two linear functions equal? when the coefficients of x are equal and the constant are equal 6. Compute (g + f )(x). ACx 1 BC 1 D 7. What type of function is the composite of two linear functions? linear 8. What is the coefficient of x in the expression for (g + f )(x)? AC 9. What is the constant term? BC 1 D 10. Compute ( f + g)(x) and express it in slope-intercept form. ACx 1 AD 1 B 11. What equation must be satisfied if f + g 5 g + f ? BC 1 D 5 AD 1 B 12. What equations must be satisfied if f + g 5 f ? AC 5 A and AD 1 B 5 B 13. What equations must be satisfied if f + g 5 g ? AC 5 C and AD 1 B 5 D 14. What must occur if f + g 5 0? AC 5 0 and AD 1 B 5 0 15. Constant functions are a subset of linear functions in which the coefficient of x is zero. What type of function is the composite of two constant functions? constant 16. a. If h(x) and k(x) are two constant functions, under what circumstances does h + k 5 k + h? if h(x) 5 k(x) b. Under what circumstances does h + k 5 k? if h(x) 5 k(x) c. Under what circumstances does h + k 5 h? h ° k always equals h d. Under what circumstances does h + k 5 0? if h(x) 5 0
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
58
Name
6-6
Class
Date
Reteaching Function Operations
When you combine functions using addition, subtraction, multiplication, or division, the domain of the resulting function has to include the domains of both of the original functions. Problem
Let f (x) 5 x2 2 4 and g(x) 5 !x. What is the solution of each function operation? What is the domain of the result? a. ( f 1 g)(x) 5 f (x) 1 g(x) 5 (x2 2 4) 1 (!x) 5 x2 1 !x 2 4 b. ( f 2 g)(x) 5 f (x) 2 g(x) 5 (x2 2 4) 2 (!x) 5 x2 2 !x 2 4 c. (g 2 f )(x) 5 g(x) 2 f (x) 5 (!x) 2 (x2 2 4) 5 2x2 1 !x 1 4 d. ( f ? g)(x) 5 f (x) ? g(x) 5 (x2 2 4)(!x) 5 x2 !x 2 4 !x
The domain of f is all real numbers. The domain of g is all x $ 0. For parts a2d, there are no additional restrictions on the values for x, so the domain for each of these is x $ 0. f f (x) (x2 2 4) !x x2 2 4 e. g (x) 5 5 5 x g(x) !x
As before, the domain is x $ 0. But, because the denominator cannot be zero, eliminate any values of x for which g(x) 5 0. The only value for which !x 5 0 is x 5 0. Therefore, f the domain of g is x . 0. f.
g g(x) !x (x) 5 5 2 f f(x) x 24
Similarly, begin with x $ 0 and eliminate any values of x that make the denominator g f(x) zero: x2 2 4 5 0 when x 5 22 and x 5 2. Therefore, the domain of f is x $ 0 combined with x 2 22 and x 2 2. In other words, the domain is x $ 0 and x 2 2, or all nonnegative numbers except 2.
Exercises Let f (x) 5 4x 2 3 and g(x) 5 x2 1 2. Perform each function operation and then find the domain of the result. 1. ( f 1 g)(x)
2. ( f 2 g)(x)
x2
1 4x 2 1; all real numbers
4. ( f · g)(x) 4x3 2 3x2 1 8x 2 6; all real numbers
2x2
1 4x 2 5; all real numbers f 5. g (x) 4x 2 3 ; x2 1 2
all real numbers
3. (g 2 f )(x) x2 2 4x 1 5; all real numbers g 6. (x) f x2 1 2 4x 2 3 ;
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
59
x u 34
Name
Class
6-6
Date
Reteaching (continued) Function Operations
• One way to combine two functions is by forming a composite. • A composite is written (g + f ) or g( f (x)). The two different functions are g and f. • Evaluate the inner function f (x) first. • Use this value, the first output, as the input for the second function, g(x). Problem
What is the value of the expression g( f (2)) given the inner function, f (x) 5 3x 2 5 and the outer function, g(x) 5 x2 1 2? 1st input x ⫽ 2
f(x)
1st output, 1, becomes 2nd input
3x ⫺ 5 3(2) ⫺ 5
g(x) x2
2nd output
⫹ 2
3
12 ⫹ 2
6 ⫺ 5
1 ⫹ 2
1 1st output
3 2nd output
Exercises Evaluate the expression g( f (5)) using the same functions for g and f as in the Example. Fill in blanks 7–14 on the chart. Use one color highlighter to highlight the first input. Use a second color to highlight the first output and the second input. Use a third color to highlight the second output, which is the answer. 1st input x ⫽ 5
f(x)
1st output,
3x ⫺ 5 10. 5) ⫺ 5 7. 3(—
10 , ——— becomes 2nd input
g(x) x2
2nd output
⫹2 14.
102 ———
2 11. 10 — ⫹2
8. 15 — ⫺ 5
12. 100 —⫹2
10 9. ———
102 13. ———
Given f (x) 5 x2 1 4x and g(x) 5 2x 1 3, evaluate each expression. 15. f (g(2)) 77
16. g( f (2.5)) 35.5
17. g( f (25)) 13
18. f (g(25)) 21
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
60
Name
Class
6-7
Date
Additional Vocabulary Inverse Relations and Functions
Choose the word or phrase from the list that best matches each sentence. inverse relation 1. In a
inverse function
one-to-one function
f21
one-to-one function
, each y-value in the range corresponds to exactly one x-value in the domain.
2. A relation pairs element a of its domain to element b of its range. The
inverse relation
pairs b with a. f21
3. The inverse of a function f is represented by
. inverse functions
4. If a relation and its inverse are functions, then they are y
.
5. Circle the inverse of y 5 2x 1 1.
y 5 x 2 12
x5222
1 y5x2 2
6. Circle the inverse of y 5 (3 2 x)2.
y 5 3 1 !x
y 5 3 2 !x
y 5 9 2 !x
7. Circle the inverse of y 5 5x2 1 4.
4 y5x2 5
y 5 "x 2 45
4 y 5 "x 2 5
8. Explain each of the steps followed to find f 21 of f (x) 5 !3x 2 2.
y 5 !3x 2 2
Replace f (x) with y.
x 5 !3y 2 2
Switch x and y.
x2 5 3y 2 2
Square both sides.
x2 1 2 5 3y
Add 2 to both sides.
2 y 5 x 31 2
Divide both sides by 3 and solve for y.
9. Find f21 for f(x) 5 4x 2 8, and explain the steps.
y 5 4x 2 8
Replace f (x) with y.
x 5 4y 2 8
Switch x and y.
x 1 8 5 4y
Add 8 to both sides.
y 5 4x 1 2
Divide both sides by 4 and solve for y.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
61
Name
Class
6-7
Date
Think About a Plan Inverse Relations and Functions
Geometry Write a function that gives the length of the hypotenuse of an isosceles right triangle with side length s. Evaluate the inverse of the function to find the side length of an isosceles right triangle with a hypotenuse of 6 in.
Know 1. An equation that relates the length of each side s and the
length of the hypotenuse h of an isosceles right triangle is 2 5 h2 z . z 2s
s
h
Need 2. To solve the problem I need to: write a function for the length of the hypotenuse in
s
of the side length and then find the inverse function for the side length in of the hypotenuse
.
Plan 3. A function that gives the length of the hypotenuse h in of the side length
z
z
s is h 5 s"2 .
4. An inverse function that gives the side length s in of the length of the
hypotenuse h is
s5 h "2
.
5. What is the value of the inverse function for h 5 6 in.? about 4.24 in.
6. Is the side length reasonable? Explain. Yes; the side length is less than the length of the hypotenuse
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
62
.
Name
Class
Date
Practice
6-7
Form G
Inverse Relations and Functions
Find the inverse of each relation. Graph the given relation and its inverse. 1.
3.
2.
4 y
x
22 21
0
1
y
23 22 21
0
x
23
22
21
0
y
22
21
0
1
x
23
21
1
2
y
21
0
1
3
2 2
21
0
1
3
y
23
21
1
2
4.
y 2
0
1
2
3
23 21
0
22
y 2 ⫺2
4
⫺4
⫺2
x
y
x
⫺4
x
x
x
23
21
0
22
y
0
1
2
3
x
23
22
21
0
y
3
2
1
0
x
3
2
1
0
y
23
22
21
0
2 ⫺2
4 y 2
2 ⫺2
⫺2 ⫺2 ⫺4
Find the inverse of each function. Is the inverse a function? 5. y 5 x2 1 2 y 5 w!x 2 2; no
6. y 5 x 1 2
8. y 5 2x2 2 3 y 5 w!2x 2 3; no
9. y 5 2x 2 1
11. y 5 5x2 y 5 w"x5; no
14. y 5 3x2 2 2
2 y 5 w"x 1 3 ; no
7. y 5 3(x 1 1)
y 5 x 2 2; yes y5
1 2x
1
1 2;
y 5 13 x 2 1; yes 10. y 5 1 2 3x2
yes
x y 5 w"1 2 3 ; no
12. y 5 (x 1 3)2 y 5 w!x 2 3; no
13. y 5 6x2 2 4
15. y 5 (x 1 4)2 2 4 y 5 w!x 1 4 2 4; no
16. y 5 2x2 1 4 y 5 w!4 2 x; no
4 y 5 w"x 1 6 ; no
Graph each relation and its inverse. 17. y 5
x13 3 6 4 2
1 18. y 5 2 x 1 5
y x
⫺4 O 2 4 6
1 20. y 5 2 x2 3 2 1 ⫺3⫺2 O ⫺2 ⫺3
19. y 5 2x 1 5 y
y 6 4 2 O ⫺6⫺4⫺2 2 ⫺2 ⫺4 ⫺6
6
x
21. y 5 (x 1 2)2 y x 1 2 3
2 O ⫺6⫺4⫺2 4 ⫺2 ⫺4 ⫺6
y
4 ⫺4 O ⫺4
x
22. y 5 (2x 2 1)2 2 2
y 2 4
x
⫺6 ⫺2 4 6
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
63
x
x 2
x 2
4
Name
6-7
Class
Date
Practice (continued)
Form G
Inverse Relations and Functions
For each function, find the inverse and the domain and range of the function and its inverse. Determine whether the inverse is a function. 1 23. f (x) 5 6 x f 21(x) 5 6x; 24. The domain and range of f and f 21 is the set of all real numbers; f 21 is a function.
f (x) 5 215 x 1 2
25. f (x) 5 x2 2 2 f 21(x) 5 w!x 1 2; 5 25x 1 10; The Domain of f 5 all real numbers 5 range domain and range of f and of f 21; Range of f 5 the set of real 21 f is the set of all real numbers greater than or equal to 22 5 numbers; f 21 is a function. domain of f 21; f 21 is not a function.
26. f (x) 5 x2 1 4 f 21(x) 5 27. w!x 2 4; Domain of f 5 all real numbers 5 range of f 21 ; Range of f 5 all real numbers greater than or equal to 4 5 domain of f 21 ; f 21 is not a function. 29. f (x) 5 3 2 x 30. 21 f (x) 5 3 2 x; the domain and range of f and f 21 is the set of all real numbers; f 21 is a function.
f (x) 5 !x 2 1 f 21(x) 5 28. f (x) 5 !3x f 21(x) 5 13 x2 ; The
f 21(x)
x2 1 1; Domain of f 5 all real numbers greater than or equal to 1 5 range of f 21 ; Range of f 5 all real numbers greater than or equal to 0 5 domain of f 21 ; f 21 is a function. f (x) 5 (x 1 1)2 f 21(x) 5 31. 21 6 !x ; domain f 5 all real numbers 5 range f 21 ; range f 5 all nonnegative real numbers 5 domain f 21 ; f 21 is not a function.
domain and range of f and f 21 is the set of all real numbers greater than or equal to 0; f 21 is a function.
f (x) 5
1 !x
f 21(x) 5 12 ; the domain and x range of f and f 21 is the set of all positive real numbers; f 21 is a function.
32. The equation f (x) 5 198,900x 1 635,600 can be used to model the number of
utility trucks under 6000 pounds that are sold each year in the U.S. with x 5 0 representing the year 1992. Find the inverse of the function. Use the inverse to estimate in which year the number of utility trucks under 6000 pounds sold in the U.S. will be 6,000,000. Source: www.infoplease.com f 21(x) 5
x 2 635,600 198,900
in 2019
33. The formula s 5 0.04n 1 2500 gives an employee’s monthly salary s, in
dollars, after selling n dollars in merchandise at an appliance store. a. Find the inverse of the function. Is the inverse a function? n 5 25s 2 62,500; yes b. Use the inverse to find the amount of merchandise sold if the employee’s salary was $2820 last month. $8000
34. The formula for the surface area A of a sphere of radius r is A 5 4pr2 for r $ 0. A a. Find the inverse of the formula. Is the inverse a function? r 5 "4p ; yes b. Use the inverse to find the radius of a sphere with surface area 10,000 m3. 28.2 m
Let f (x) 5 2x 1 5. Find each value. 35. ( f 21 + f )(21) 21
36. ( f + f 21)(3) 3
1 1 37. ( f + f 21) Q 22 R 22
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
64
Name
Class
Date
Practice
6-7
Form K
Inverse Relations and Functions
Find the inverse of each relation. Graph the given relation and its inverse. 1.
x
y
0
2.
x
y
21
22
1
1
2 3
x 21 1 3 5
3.
x
y
7
23
2
0
3
22
2
3
2
7
21
2
5
4
19
0
2
y 0 1 2 3
6
y
x 7 3 7 19
4 2 O
x 2
4
6
y 22 0 2 4
15
y
x 2 2 2 2
10 5 O
x 5 10 15
4 y
y 23 22 21 0
⫺4 ⫺2 O ⫺2 ⫺4
Find the inverse of each function. Is the inverse a function? To start, switch x and y. x 4. y 5 2 y x 5 2 y 5 2x; yes
5. y 5 x2 1 4
6. y 5 (3x 2 4)2
y 5 w!x 2 4; no
y5w
!x 1 4 ; 3
no
Graph each relation and its inverse. 8. y 5 2x2
7. y 5 3x 2 4 4 y
4 y
2 ⫺4 ⫺2 O ⫺2 ⫺4
9. y 5 (3 2 2x)2
x 2
4
2 ⫺2 ⫺2
y 6
O 2
x 4
4 2 O
⫺4
2
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
65
4
6 x
x 4
Name
Class
6-7
Date
Practice (continued)
Form K
Inverse Relations and Functions
Find the inverse of each function. Is the inverse a function? 10. f (x) 5 (x 1 1)2 y 5 w!x 2 1; no
2x3 11. f (x) 5 5
12. f (x) 5 !3x 1 4
y 5 3Å52 x; yes
y5
(x 2 4) 2 ; 3
yes
13. Multiple Choice What is the inverse of y 5 5x 2 1? B
f 21(x) 5 5x 1 1
f 21(x) 5
x11 5
x
x
f 21(x) 5 5 1 1
f 21(x) 5 5 2 1
For each function, find its inverse and the domain and range of the function and its inverse. Determine whether the inverse is a function. 14. f (x) 5 !x 1 1 15. f (x) 5 10 2 3x 16. f (x) 5 4x2 1 25 10 1 21 2 21 !x 2 25 f (x) 5 x 2 1; domain f (x) 5 23 x 1 3 ; domain f21(x) 5 w ; domain 2 f(x): x L 21, range f(x): all real numbers; range f(x): all real numbers; f(x): y L 0; domain f 21 : range f(x): y L 25; domain f(x): all real numbers; x L 0, range f 21 : y L 21; 21 : all real domain f f 21: x L 25; range f 21 : all the inverse is a function. numbers; range f 21 : all real real numbers; the inverse is numbers; the inverse is a not a function. function. 17. The formula for the area of a circle is A 5 pr2 . a. Find the inverse of the formula. Is the inverse a function? r 5 ÅA p ; yes b. Use the inverse to find the radius of a circle that has an area of 82 in.2. about 5.1 in.
For Exercises 18−20, f (x) 5 5x 1 11. Find each value. To start, rewrite f (x) as y and switch x and y. 18. A f f 21 B(5)
19. A f 21 f B(23)
°
°
y 5 5x 1 11 5
20. A f 21 f B(0)
°
0
23
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
66
Name
Class
6-7
Date
Standardized Test Prep Inverse Relations and Functions
Multiple Choice For Exercises 1−4, choose the correct letter. 1. What is the inverse of the relation?
x y
y
22 21 3
0
2
A
1 21 22
3
x
22 21
0
2
0 21 22
y
22 21
1
3
22 21
1
22 21 2
x
x
⫺2 ⫺1
0
2
x
y
⫺3 ⫺1
1
2
y
2
1
3
1 21 22
2. What is the inverse of the function? y 5 5(x 2 3) G
y5
x13 5
y 5 15 x 1 3
y 5 5(x 1 3)
y 5 15 x 2 3
3. What function with domain x $ 5 is the inverse of y 5 !x 1 5? C
y 5 x2 1 5
y 5 x2 2 5
y 5 (x 2 5)2
y 5 (x 1 5)2
4. What is the domain and range of the inverse of the function? y 5 !x 2 5 F
domain is the set of all real numbers $ 0; range is the set of all real numbers $ 5 domain is the set of all real numbers $ 5; range is the set of all real numbers $ 0 domain and range is the set of all real numbers $ 5 domain and range is the set of all real numbers
Extended Response 5. A high school principal uses the formula y 5 150x 1 180 to predict a
student’s score on a state achievement test using the student’s 11th-grade GPA number x. a. What is the inverse of the formula? b. Is the inverse a function? c. Using the inverse, what GPA does a student need to get a ing score of 510 on the state exam? 1 1 [4] a. y 5 150 (x 2 180) or y 5 150 x 2 65 b. yes c. 2.2 [3] most work is correct but there are minor errors [2] student understands the problem and shows some correct work [1] student may understand the problem but doesn’t know how to proceed OR correct answers without work shown [0] no answers given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
67
Name
6-7
Class
Date
Enrichment Inverse Relations and Functions
Composition, Inverses, and Linear Functions Solving an equation for one variable in of another is an important step in finding inverses. This step is also used in conversion formulas. Consider the following linear functions. Let F denote the temperature in degrees Fahrenheit, C the temperature in degrees Celsius, and K the temperature in degrees Kelvin. The formula for converting degrees Fahrenheit to degrees Celsius is C 5 59 (F 2 32), and the formula for converting degrees Celsius to degrees Kelvin is K 5 C 1 273. 1. Use composition to determine the formula for converting degrees Fahrenheit
to degrees Kelvin. K 5 5(F 2 32) 1 273 9 2. Solve this function for F. F 5 95 (K 2 273) 1 32 3. This new equation converts degrees
Kelvin
to degrees Fahrenheit .
9 4. Derive a formula to convert degrees Celsius to degrees Fahrenheit. F 5 5C 1 32
5. Derive a formula to convert degrees Kelvin to degrees Celsius. C 5 K 2 273 6. Compose these two functions to find a formula for converting degrees Kelvin to degrees Fahrenheit. F 5 95 (K 2 273) 1 32
Solve each of the following problems involving functions. 7. In 1940, the cost of a new house was $10,000. By 1980, this cost had risen to
$90,000. Assuming that the increase is linear, find a function expressing the cost c of a new house in of the year y. Solve this function for y. What does this new function enable you to do? c 2 10,000
c 5 10,000 1 2000( y 2 1940); y 5 2000 1 1940; find the year given the cost of a house 8. Between the ages of 5 and 15, a typical child grows at a fixed annual rate. If Mary
was 42 in. in height when she was 5 yr old and grew at a rate of 2 in. a year, find a formula that expresses Mary’s height h in inches when her age is a years. Solve this function for a. What does this new function enable you to do?
h 5 2(a 2 5) 1 42; a 5 h 22 42 1 5; compute Mary’s age given her height 9. The air temperature, in degrees Fahrenheit, surrounding an airplane on one
1 particular day was modeled by T 5 2200 a 1 110, where a is the altitude, in feet, of the airplane. Solve this function for a. What does this new function enable you to do?
a 5 200(2T 1 110); find the altitude of the airplane given the temperature 10. The formula L 5 0.25W 1 0.5 models the length of a certain spring, in inches,
when a weight of W ounces is attached to it. Solve this function for W. What does this new function enable you to do? 2 0.5 W 5 L 0.25 ; find the weight attached to the spring given the length of the stretched spring
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
68
Name
Class
Date
Reteaching
6-7
Inverse Relations and Functions
•
Inverse operations “undo” each other. Addition and subtraction are inverse operations. So are multiplication and division. The inverse of cubing a number is taking its cube root.
•
If two functions are inverses, they consist of inverse operations performed in the opposite order.
Problem
What is the inverse of the relation described by f (x) 5 x 1 1? f (x) 5 x 1 1 y5x11
Rewrite the equation using y, if necessary.
x5y11
Interchange x and y.
x215y
Solve for y.
y5x21
The resulting function is the inverse of the original function.
So, f 21 (x) 5 x 2 1.
Exercises Find the inverse of each function. 2. y 5 3x3 1 2
1. y 5 4x 2 5 f 21 5
x 1 5 4
f 21 5
4. y 5 0.5x 1 2 f 21
5 2x 2 4
x 7. f (x) 5 5 f 21(x) 5 5x
3. y 5 (x 1 1)3
3 2 "x 2 3
3
f 21 5 "x 2 1
5. f (x) 5 x 1 3 f 21(x) 5 x 2 3
6. f (x) 5 2(x 2 2)
8. f (x) 5 4x 1 2
9. y 5 x
f 21(x)
4 f 21(x) 5 x 1 2
x22 4
5 x21 10. y 5 x 2 3 11. y 5 2 f 21 5 x 1 3 f 21 5 2x 1 1 2 13. f (x) 5 !x 1 2 14. f (x) 5 3 x 2 1 f 21(x) 5 32(x 1 1) f21 (x) 5 x2 2 2 for x L 22 16. f (x) 5 2(x 2 5)2 f 21(x)
556
"x2
17. y 5 !x 1 4 f 21
5 (x 2
4)2
f 21 5 x 12. y 5 x3 2 8 3
f 21 5 "x 1 8
x13 5 f 21(x) 5 5x 2 3
15. f (x) 5
18. y 5 8x 1 1 for x L 0
1 f 21 5 x 2 8
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
69
Name
6-7
Class
Date
Reteaching (continued) Inverse Relations and Functions
Examine the graphs of f (x) 5 !x 2 2 and its inverse, f 21(x) 5 x2 1 2, at the right.
6 5 4 3 2 1
Notice that the range of f and the domain of f 21 are the same: the set of all real numbers x $ 0. Similarly, the domain of f and the range of f 21 are the same: the set of all real numbers x $ 2.
y
f ⫺1
f x
O
1 2 3 4 5 6
This inverse relationship is true for all relations whenever both f and f 21 are defined. Problem
What are the domain and range of the inverse of the function f (x) 5 !3 2 x? f is defined for 3 2 x $ 0 or x # 3. Therefore, the domain of f and the range of f 21 is the set of all x # 3. The range of f is the set of all x $ 0. So, the domain of f 21 is the set of all x $ 0.
f
6 5 4 3 2 1
23 22 21 O
Exercises
y
x 1 2 3
Name the domain and range of the inverse of the function. 1 19. y 5 2x 2 1 20. y 5 2 2 x The domain and the range is domain: x u 2; the set of all real numbers. range: y u 0
21. y 5 !x 1 5 domain: x L 0; range: y L 25
22. y 5 !2x 1 8 domain: x L 8; range: y K 0
23. y 5 3 !x 1 2 domain: x L 2; range: y L 0
24. y 5 (x 2 6)2 domain: x L 0; range: all real numbers
25. y 5 x2 2 6
1 26. y 5 x 1 4
27. y 5
domain: x L 26; range: all real numbers
domain: x u 0; range: y u 24
1 (x 1 4)2 domain: x S 0; range: y u 24
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
70
Name
6-8
Class
Date
Additional Vocabulary Graphing Radical Functions
1. Circle the radical functions in the group below.
y 5 2(x 1 5) 2 3
y 5 22 !x 2 4
y5x24
3 y5 ! x18
2. Circle the square root functions in the group below. 3 y5 ! x22
y 5 !x 1 4
y 5 2 !x 2 3
y 5 3(x 1 6)
For Exercises 3−8, draw a line from each word or phrase in Column A to its matching item in Column B. Column A
Column B
3. parent function
A. y 5 !x 2 k
4. translate k units downward
B. y 5 2!x
5. stretch vertically by the factor k (k . 1)
C. y 5 !x 2 k
6. translate k units upward
D. y 5 !x
7. reflection in x-axis
E. y 5 k !x
8. translate k units to the right
F. y 5 !x 1 k
Identify the meaning of the following in the function y 5 2!x 2 4 1 5. 9. 2:
Stretch vertically by a factor of 2
.
10. 4:
Translate 4 units to the right
.
11. 5:
Translate 5 units upward
.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
71
Name
6-8
Class
Date
Think About a Plan Graphing Radical Functions
Electronics The size of a computer monitor is given as the length of the screen’s 5 diagonal d in inches. The equation d 5 6 !3A models the length of a diagonal of a monitor screen with area A in square inches.
a. Graph the equation on your calculator.
b. Suppose you want to buy a new monitor that has twice the area of your old
monitor. Your old monitor has a diagonal of 15 inches. What will be the diagonal of your new monitor?
1. How can you use a graph to approximate the area of the old monitor? Graph the equation and graph y 5 15. The x-coordinate of their intersection will be the area of the old monitor
.
2. Graph the equation on your calculator. Make a sketch of the
graph.
d 40 30
3. What is the area of the old monitor? 108 in.2
4. How can you check your answer algebraically?
20 10 0
0
100 200 300 400
Substitute 15 for d and solve the equation for A
A
.
5. Show that your answer checks. 15 5 56"3A, 15 Q 65 R 5 "3A, 18 5 "3A, 182 5 3A, 324 5 3A, A 5 108 6. How can you find the diagonal of a new monitor with twice the area of the old
monitor? Substitute 2 times the area of the old monitor for A in the equation
7. Use your method to find the diagonal of your new monitor. d55 "3A 5 56"3 ? 2 ? 108 5 56"648 N 21.2 in. 6 8. What will be the diagonal of your new monitor? about 21.2 in.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
72
.
Name
Class
Date
Practice
6-8
Form G
Graphing Radical Functions
Graph each function. 1. y 5 !x 1 3
2. y 5 !x 2 1
8 y 6 4 2
6 y
4
4
2 x
O
2
4
6
4. y 5 !x 2 3
O ⫺2 ⫺6 ⫺4 ⫺8
2
x 4 6 8
2
4 6
2
2
1 6. y 5 4 !x 2 1 1 5
y
4
x
⫺4 ⫺2 O ⫺2
5. y 5 22 !x 2 2
6 y
O
1
x 2 4 6 8
O ⫺2
8
3. y 5 !x 1 5
6 y
8 6 4 2
x
y
O
x 2 4 6 8
Solve each square root equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 7. !x 1 6 5 9 75
no solution; 32 9. !3x 2 5 5 !1 2 x is extraneous
8. !4x 2 3 5 5 7
r
A 10. If you know the area A of a circle, you can use the equation r 5 to find Äp the radius r. a. Graph the equation. b. What is the radius of a circle with an area of 350 ft2? about 10.6 ft
12 8 4 A
Graph each function. 3
3
y
O ⫺2
13. y 5 !x 1 3 2 1
2 2
x
⫺2
O
2 2
x
⫺4
⫺2
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
73
100
y
y
2 ⫺2
3
12. y 5 2 !x 2 3
11. y 5 2!x 1 2
O
⫺2
O ⫺2
2 x
200
300
Name
6-8
Class
Date
Practice (continued)
Form G
Graphing Radical Functions
Rewrite each function to make it easy to graph using transformations of its parent function. Describe the graph. 14. y 5 !81x 1 162
15. y 5 2!4x 1 20
y 5 9 !x 1 2; graph of y 5 9 !x shifted left 2 units 17. y 5 2!64x 1 192
y 5 22 !x 1 5; graph of y 5 22 !x shifted left 5 units 3
18. y 5 2!8x 2 56 1 4
y 5 28 !x 1 3; graph of y 5 28 !x shifted left 3 units 20. y 5 !0.25x 1 1
3
16. y 5 !125x 2 250 3 y 5 5 !x 2 2; graph of 3 y 5 5 !x shifted right 2 units
19. y 5 !25x 1 75 2 1
y 5 5 !x 1 3 2 1 ; graph of y 5 5 !x shifted left 3 units
3
y 5 22 !x32 7 1 4 ; graph of y 5 22 !x shifted right 7 units and up 4 units 21. y 5 5 2 !4x 1 2
y 5 0.5 !x 1 4; graph of y 5 0.5 !x shifted left 4 units
y 5 5 2 2"x 1 12; graph of y 5 22 !x shifted left 12 unit and up 5 units
and down 1 unit 3
22. y 5 !27x 2 54 3 y 5 3 !x 2 2; graph of 3 y 5 3 !x shifted right 2 units
3 3V 23. To find the radius r of a sphere of volume V, use the equation r 5 Å 4p . a. Graph the equation. b. A balloon used for advertising special events has a volume of 225 ft3. What is the radius of the balloon? 3.77 ft
24. An exercise specialist has studied your exercise routine and says the
formula t 5 1.85 !c 1 10 expresses the amount of time t, in minutes, it takes you to burn c calories (cal) while exercising. a. Graph the equation. b. According to this formula, how long should it take you to burn 100 cal? 200 cal? 300 cal? 19.4 min, 26.8 min, 32.6 min 25. You can use the equation t 5
1 4 !d
to find the time t, in seconds, it takes an object to fall d feet after being dropped. a. Graph the equation. b. How long does it take the object to fall 400 feet? 5 s
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
74
5 4 3 2 1
r
V O 100 300 500 50 40 30 20 10
t
O 100 10 t 8 6 4 2 O 200
c 400
d 800
Name
Class
Date
Practice
6-8
Form K
Graphing Radical Functions
Graph each function. 1. y 5 !x 1 3 6
2. y 5 !x 2 4
y
6
4
3. y 5 !x 2 7
y
y O ⫺2
4
2
2
x
O
2
4
x
O
6
2
4
6
x 2
4
6
⫺4 ⫺6
Graph each function. 4. y 5 4 !x 6
5. y 5 22 !x 1 1
y
y
4
O ⫺2
2
⫺4
x
O
2
4
x 2
4
6
4 y 2 O ⫺2
⫺6
6
6. y 5 5 !x 2 4
x 2
4
6
⫺4
Solve each square root equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 7. !x 1 2 5 7 47 8 6 4 2 O
y
8. !4x 1 1 5 5 6 6
9. 3 !3 2 x 5 10 28.11 y
y 9
4 x 10 20 30 40
6
2 O
x 2
4
6
3
10. A periscope on a submarine is at a height h, in feet, above the surface of the water. The
greatest distance d, in miles, that can be seen from the periscope on a clear day is given 3h
by d 5 Å 2 . a. If a ship is 3 miles from the submarine, at what height above the water would the submarine have to raise its periscope in order to see the ship? 6 ft b. If a ship is 1.5 miles from the submarine, to what height would it have to be raised? 1.5 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
75
Name
Class
Date
Practice (continued)
6-8
Form K
Graphing Radical Functions
3 Graph each function. To start, graph the parent function, y 5 ! x. 3
1 3 13. y 5 2 !x 2 1 1 3
3
12. y 5 3 2 !x 1 1
y
y 6
y 6
4
4
11. y 5 !x 2 4 ⫺2 ⫺2
x
2
⫺4 ⫺6
⫺2
2
x
⫺2
x
2
14. A center-pivot irrigation system can water from 1 to 130 acres of crop land.
The length l in feet of rotating pipe needed to irrigate A acres is given by the function l 5 117.75!A. a. Graph the equation on your calculator. Make a sketch of the graph. b. What length of pipe is needed to irrigate 40, 80, and 130 acres? 744.7 ft, 1053.2 ft, 1342.6 ft
300
y
200 100 ⫺4 ⫺2 O
Graph each function. Find the domain and range. 3
3
15. y 5 2 !x 2 4
16. y 5 2!8x 1 5 y
4 y 2 O
12 8 4
x 2
4
6
⫺2 O ⫺8
2
x
domain: all real numbers; range: all real numbers
domain: all real numbers; range: all real numbers
17. y 5 23 !x 2 4 2 3 y 4 2 O 4 ⫺2 2 ⫺4 ⫺6 ⫺8
x 6 8
domain: x L 4; range: y K 23
18. Open Ended Write a cube root function in which the vertical translation of 3 y5 ! x is twice the horizontal translation. Answers may vary. Any cube root 3
function in the form y 5 a !x 2 h 1 k where k 5 2h.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
76
x 2
4
Name
Class
Date
Standardized Test Prep
6-8
Graphing Radical Functions
Multiple Choice For Exercises 1−4, choose the correct letter. 1. What is the graph of y 5 !x 1 4? C 8 6 4
y
x ⫺4⫺2 O
2 4
8 6 4 2 O
y
x 2 4 6 8
8 6 4 2
y
8 6 4
y
x
x ⫺4⫺2 O
2 4 6 8
O
2 4
2. What is the graph of y 5 !x 2 3 2 2? F y
y 4 2
1 O
8x
2 4
⫺2 ⫺3
⫺4
2 4 x
⫺2 ⫺4
6 4 2 O
y x 2 4 6 8
⫺4
8 6 4 2 O
y
x 2 4 6 8
3 3. What is the graph of y 5 1 2 !x 1 3? D
4 ⫺6⫺4⫺2 ⫺2 ⫺4
y x O
4 2 ⫺4⫺2 ⫺2 ⫺4
y x 2 4
4 2
y
⫺8⫺6⫺4⫺2 O x ⫺4
y
4 2
x
⫺6⫺4⫺2 ⫺2 ⫺4
2
4. What is the description of y 5 !9x 2 3 to make it easy to graph using transformations of its parent function? G
the graph of y 5 3 !x, shifted right 3 units the graph of y 5 3 !x, shifted right 13 unit the graph of y 5 !x, shifted right 3 units and up 9 units the graph of y 5 !x, shifted right 13 unit and up 9 units
6 y 4
Short Response
2
5. What is the graph of y 5 2 !x 2 1 1 3?
O
[2] The graph is correct. [1] One of the transformations (horizontal, vertical, or stretch) is incorrect. [0] no answer given Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
77
x 2
4
6
Name
Class
Date
Enrichment
6-8
Graphing Radical Functions
Transformations of Other Functions You can obtain the graph of any function of the form y 5 a ? f(x 2 h) 1 k by using the shifting rules similar to those used to obtain the graph of y 5 a!x 2 h 1 k. Note that the second function is a special case of the first when f(x) 5 !x. To obtain the graph of y 5 a ? f(x 2 h) 1 k, given the graph of y 5 f(x), use the following general rules: • If a , 0, reflect the graph of y 5 f(x) across the x-axis. • If ua u . 1, the graph of y 5 f(x) is stretched by a factor of a. • If 0 , ua u , 1, the graph of y 5 f(x) is compressed by a factor of a. • The graph of y 5 f(x) is shifted right h units if h . 0 and left h units if h , 0. • The graph of y 5 f(x) is shifted up k units if k . 0 and down k units if k , 0. 1. Use the general rules to describe how the graph of y 5 23(x 2 5)2 1 7 can
be obtained from the graph of f(x) 5 x2 . reflect across the x-axis, stretch by a factor of 3, shift right 5 units and shift up 7 units 3
2. Write the equation for the graph that looks like y 5 !x but that is shifted
right four units, reflected across the x-axis, and shifted down six units. 3
y 5 2!x 2 4 2 6 3. Use the graph of y 5 f(x) given below to sketch the graph of y 5 f(x 1 2) 2 1. y
6 4 2
y ⴝ f (x)
4
x ⫺4
O
4
⫺6 ⫺4 ⫺2 O
⫺4
y
y 4 x 2 4 6
⫺4 ⫺6
x O
⫺4
4
⫺4
4. The graph of y 5 f(x) and y 5 g(x) is given below. The graph of g is a transformation of the graph of f. Write the equation for the graph of g in of f. g(x) 5 f(x 1 1) 23 y f
2
x
O ⫺2
2 ⫺2 g
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
78
Name
Class
6-8
Date
Reteaching Graphing Radical Functions
The graph of y 5 a!x 2 h 1 k is a translation h units horizontally and k units vertically of y 5 a!x. The value of a determines a vertical stretch or compression of y 5 !x. Problem 6
What is the graph of y 5 2 !x 2 5 1 3?
y
4
y 5 2 !x 2 5 1 3
2 x
a52
O
h55 k53
2
4
6
Translate the graph of y 5 2 !x right five units and up three units. The graph of y 5 2 !x looks like the graph of y 5 !x with a vertical stretch by a factor of 2.
Exercises Graph each function. 1. y 5 !x 2 4 1 1 4 y
2. y 5 !x 2 4
2 O
2
3. y 5 !x 1 1
5. y 5 2 !x 2 1
7. y 5 2!x 1 1
6. y 5 22 !x 1 3 1 4
y 2
2
2 y
8. y 5 !x 1 3 2 4
x
y ⫺4 ⫺2 O ⫺2
4
⫺4
⫺4 6 y
10. y 5 2!x 2 2
4 2 O
x
⫺4 ⫺2 O
O ⫺2
9. y 5 3 !x 1 2
6 y 4
x
⫺2 O ⫺2
2
4
x
⫺4 ⫺2 O ⫺2
2
2
y
4. y 5 2!x 1 2 2 3 x
⫺2 O ⫺2
2
⫺4
y
2
x
⫺2 O ⫺2
x 6
4
y
x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
79
x
Name
6-8
Class
Date
Reteaching (continued) Graphing Radical Functions
Graphs can be used to find solutions of equations containing radical expressions. Problem
What is the minimum braking distance of a bicycle with a speed of 22 mph? You can find the minimum braking distance d, in feet, of a bicycle travelling s miles per hour using the equation s 5 5.5 !d 1 0.002 . We want to find the value of d when s 5 22. In other words, solve the equation 5.5 !d 1 0.002 5 22. Graph Y1=5.5√(X+0.002) and Y2=22. Try different values until you find an appropriate window. Then use the intersect feature to find the coordinates of the point of intersection.
Intersection x ⫽ 15.998 Y ⫽ 22
The minimum braking distance will be about 16 ft.
Exercises Solve the equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 11. !3x 1 1 5 5 8
12. !4x 1 1 5 9 20
13. !2 2 5x 5 4 22.8
14. !3x 1 5 5 7 14.67
15. !7x 1 2 5 11 17
16. !2x 2 1 5 !1 2 2x 0.5
17. !x 2 2 5 !2 2 3x no solution; x 5 1 is extraneous
18. 7!x 2 3 5 2!2x 1 1 3.68
19. !2x 2 5 5 !4 2 x 3
20. !2x 1 7 5 3!5x 1 2 20.26
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
80
Name
Class
Date
Chapter 6 Quiz 1
Form G
Lessons 6-1 through 6-4 Do you know HOW? Find all the real roots. 1. !36 26, 6
8 4. 3 2 Å 125
3
2. !0.25 20.5, 0.5
3. !264 24
225
Simplify each radical expression. Use absolute value symbols when needed. 2 6. "49x4 7x
5. "25y2 5|y|
2 3 8. " 20.125y6 –0.5y
3 3 7. " 28x9 22x
Find the two real solutions of each equation. 2 2 9. 9x2 2 4 5 0 23, 3
10. x4 5 0.0016 20.2, 0.2
Multiply or divide and simplify. Assume that all variables are positive. 11. 2 !2x ?
3 " 4xy7
"18xy2 12xy
12. 3 "32x4y4
y 2x
Simplify. Rationalize all denominators. 13. 3 !180 1 !45 2 8 !20 5 !5
14.
5 1 !3 2 2 !3
13 1 7 !3
Simplify each expression. 2
15. (2125)3 25
3
17. 320.6 8
16. 814 27
18. 491.5 343
Do you UNDERSTAND? 19. Geometry What is the perimeter of the triangle at the right? 27 2 !2 7
2
2
3 V2
3 V2
20. Reasoning Solve. !75 1 !3x 5 12 !3 49
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
81
5 3 V2
Name
Class
Date
Chapter 6 Quiz 2
Form G
Lessons 6-5 through 6-8 Do you know HOW? Solve. Check for extraneous solutions. 1. !x 2 2 5 x 2 8 11
2. !x 1 4 5 !3x 2 2 3
Let f (x) 5 x2 2 x 2 12 and g (x) 5 x 2 4. Perform each function operation and then find the domain. 3. f (x) 2 2g(x) x2 2 3x 2 4; all real numbers 4. f (x) ? g (x) x3 2 5x2 2 8x 1 48; all real numbers f (x) g (x) 1 x 1 3; x u 4 5. 6. g (x) f (x) x 1 3; x u 4 and x u 23
Let f (x) 5 2x 2 5 and g (x) 5 x2 . Find each composition. 7. ( f + g)(x) 2x2 2 5
8. (g + f )(x) 4x2 2 20x 1 25
Find the inverse of each function. Is the inverse a function? x 3 9. g(x) 5 "2 2 3 g21(x) 5 2x2 1 6, x L 6; 10. h(x) 5 5 2 x3 h21(x) 5 ! 5 2 x; yes yes
Graph. Find the domain and range of each function. 11. y 5 2 2 !x
12. y 5 !x 2 1 1 1
6 y 4
domain: x L 0, range: y K 2
2 O
4
4
domain: x L 1, range: y L 1
x 2
6 y 2 O
6
x 2
4
Do you UNDERSTAND? 13. Writing Explain why it is not true that !22 ? !22 5 !4, even though
(22) ? (22) 5 4. Answers may vary. Sample: !22 ? !22 5 i!2 ? i!2 5 i2(!2)2 5 (21)(2) 5 22 u !4 14. Reasoning Suppose the cost of an item is x dollars. It is marked up by n% and,
later, that new cost is reduced by n%. Is the final cost equal to x dollars? Use a composition of functions to justify your answer. No; answers will vary. Sample: Let n 5 20, then f(x) 5 1.2x and g(x) 5 0.8x and (g f)(x) 5 0.8(1.2x) 5 0.96x.
°
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
82
6
Name
Class
Date
Chapter 6 Test
Form G
Do you know HOW? Simplify each radical expression. Use absolute value symbols when needed. 1. "400x2y6 20»xy3… 3
3
4. " 64a6b2
4a2 "b2
3
4
2. " 2125a9 25a3
4 3. " 81x5y9 3»x…y2 "xy
5. "50s2t4 5»s…t2 !2
6. "256x16y28 16x8y14
Simplify each expression. Rationalize all denominators. Assume that all variables are positive. 7.
"200x3y "2xy5
8. Q 8 2 3 !2 R Q 8 1 3 !2 R 46
10x y2
10. "8x3 ? "2x5 4x4 13.
2 22 1 2 !2 1 1 !2
9.
1 !3 1 5
5 2 !3 22
3
3 3 !2 1 1 !4 1 !2 11. !63 1 2 !28 2 5 !7 2 !7 12. 3 2 !4
4
4 !5 !20 14. 4 2 !4
15. !15 Q 1 2 !45 R !15 2 15 !3
Simplify each expression. Assume that all variables are positive. 16.
16x5y10
Q 81xy2 R
19. Q 4x22y4 R
3 4
2
8x3y6 27 1
22
2
1
17. (264)23 16
x 2y2
20. Q 8ab2 R
1
22
1
7
18. a3 ? a2 a6 1
Q 8ab2 R 2 1
2 1
1 1
9 5
21. Q s5 t3 R Q s2 t2 R s10t6
Solve each equation. Check for extraneous solutions. 3
22. !x 2 3 5 1 4 1
25. (2x 1 1)3 5 3 13
23. !x 1 7 5 x 1 1 2
24. !3x 2 8 5 2 4
26. "x2 2 5 5 4 w"21
27. 3(x 1 1)3 5 48 29, 7
4
Let f(x) 5 x2 1 5 and g(x) 5 x 2 7. Perform each function operation and then find the domain. 2 f (x) x 1 5 ; all real x 27 28. g (x) numbers except 7
29. f (x) 2 2g (x) x2 2 2x 1 19; 30. f (x) ? g(x) all real numbers x3 2 7x2 1 5x 2 35; all real numbers For each pair of functions, find (f + g)(x) and (g + f )(x). 31. f(x) 5 3x 1 5, g(x) 5 x2 1 1
32. f(x) 5 x2 2 5x 1 2, g(x) 5 2x
3x2 1 8; 9x2 1 30x 1 26
4x2 2 10x 1 2; 2x2 2 10x 1 4
33. f(x) 5 !2x 2 1, g(x) 5 5x 1 3 !10x 1 5; 5 !2x 2 1 1 3
34. f(x) 5 22x2, g(x) 5 x 1 4 22x2 2 16x 2 32; 22x2 1 4
Let f(x) 5 5x 2 4 and g(x) 5 x2 2 1. Find each value. 35. (g + f )(21) 80
36. (f + g)(2) 11
37. (g + f )(0) 15
38. f(g(!6)) 21
39. f(g(0)) 29
4 40. g Q f Q 5 R R 21
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
83
Name
Class
Date
Chapter 6 Test (continued)
Form G
Find the inverse of each function. Is the inverse a function? 43. f(x) 5 !x 1 4 f21(x) 5 x2 2 4, x L 24; yes
41. f(x) 5 (x 1 2)2 2 4 42. f(x) 5 4x3 2 1 21 3 1 f (x) 5 w!x 1 4 2 2; no f21(x) 5 %x 1 4 ; yes 2 44. f(x) 5 3x 1 2 45. f(x) 5 x 2 5 2 f21(x) 5 x 2 3 ; yes
3
46. f(x) 5 !x 1 2 f21(x) 5 x3 2 2; yes
f21(x) 5 w!x 1 5; no
Graph. Find the domain and range of each function. 1 47. y 5 !x 2 1 1 2 48. y 5 2!x 1 3 2 1 49. y 5 2 !x 1 3 50. y 5 2!x 1 4 2 1 domain: x L 24; domain: x L 1; domain: x L 23; domain: x L 0; range: y K 21 range: y L 2 range: y K 21 range: y L 3 4
y
y
2 O
4
4 2 O 2
x 2
x
2
4
4
yx
y
O
x 2
4
4 2 O 2 4
Rewrite each function to make it easy to graph using transformations. Describe the graph. 3
51. y 5 !9x 2 63 1 4 y 5 3 !x 2 7 1 4; graph of y 5 3 !x shifted right 7 units and up 4 units
52. y 5 !8x 2 64 2 5 3
3
53. y 5 !227x 2 27 1 4 3
3
y 5 2 !x 2 8 2 5; graph of y 5 2 !x shifted right 8 units and down 5 units 54. y 5 !16x 2 32 y 5 4 !x 2 2; graph of y 5 !x shifted right 2 units
3
y 5 23 !x 1 1 1 4; graph of y 5 23 !x shifted left 1 units and up 4 units
55. The children’s park has become very popular since your club built new play equipment. Use the equation f 5 4!A to calculate the amount of fence f you
need to buy based on the area A of the playground. a. The park currently has an area of 8100 ft2. How many feet of fencing currently encloses the park? 360 ft b. Suppose you want to increase the fenced play area to four times its current area. If you can reuse the fencing already at the park, how much new fencing do you need to buy? 360 ft
Do you UNDERSTAND? 1
1
56. Writing Explain under what circumstances 2xn 5 (2x)n and provide an 1 1 example to justify your answer. n is an odd integer; answers may vary. Sample: 283 5 22 5 (28)3 3
57. Reasoning Graph y 5 !x and y 5 !x on the same coordinate grid. Notice 3 that for 0 , x , 1, the graph of y 5 !x lies below the graph of y 5 ! x but the opposite is true for x . 1. Explain why this is the case. Give an example. 1
Answers may vary. Sample: xn grows more rapidly (that is, as n increases) for 1 1 x R 1 and grows more slowly for x S 1; for example, Å64 5 18 R 14 5 3Å64 but 3
!64 5 8 S 4 5 !64.
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
84
Name
Class
Date
Chapter 6 Quiz 1
Form K
Lessons 6–1 through 6–4 Do you know HOW? Find each real root. 1. !49 7
3
2. !0.36 0.6
3. !2125 –5
Simplify. Assume that all variables are positive. 3
4. "600x6y3 10x3y !6y
4
5. " 54xy5
6. " 64x4y8 4 2xy2 !4
3
3y "2xy2
Divide and simplify. 7.
3
"20x3 "5x 2x
8.
"56x4y
9.
3
"7x3y 3
2 !x
"32a7b2 "2a3b 4a2 !b
Simplify. 10. !7 1 3 !7 4 !7
11. !18 1 !32 7 !2
3
3
12. 2 !24 2 !81 3
!3
Write each expression in radical form. 3
1
13. x3
15. x1.5
14. x4 4
3
x"x
"x 3
!x
Write each expression in exponential form. 3
16. " 4x2 Q4x2R
18. "65x4y
17. !5ab
1 3
1 (5ab) 2
1
x 2(65y) 2
Do you UNDERSTAND? 19. Writing Explain when absolute value symbols are needed when you are n simplifying radical expressions. For radicals in the form "a m , if the index is even, use absolute value symbols. If the index is odd, you don’t need absolute value symbols for any . 20. An object is moving at a speed of A5 2 !3B mi/h. How long will it take the
object to travel 35 mi? 175 1 35 !3 22
h Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
85
Name
Class
Date
Chapter 6 Quiz 2
Form K
Lessons 6–5 through 6–8 Do you know HOW? Solve. Check for extraneous solutions. 1. 4 !x 2 2 5 2 x 5 1
2. !x 1 5 5 4 x 5 11
3. !5x 2 1 1 3 5 x x 5 10
4. !2 2 x 2 x 5 4 x 5 22
Let f (x) 5 x2 2 x and g (x) 5 2x 2 2 . Perform each function operation and then find the domain of the result. f f x 5. (f 1 g)(x) (f 1 g)(x) 5 x2 2 x 2 2; 6. a g b (x) a g b (x)5 2 ; all real numbers except x 5 21
all real numbers
Find the inverse of each function. Is the inverse a function? 3
8. y 5 (x 2 2)3 1 1 y 5 !x 2 1 1 2; yes
7. y 5 x2 2 3 y 5 6 "x 1 3 ; no
Graph each function. 2 9. y 5 3 !x
6
y
4 2 O
domain: x L 0 range: y L 0
3
10. y 5 2!8x 1 5
6
y
4 2
x
2 4 6
2 O
x
2
domain: all real numbers range: all real numbers
Do you UNDERSTAND? 11. Multiple Choice The graph of y 5 2!x is shifted 4 units up and 3 units right. Which equation represents the new graph? B
y 5 2!x 2 4 1 3
y 5 2!x 1 3 1 4
y 5 2!x 2 3 1 4
y 5 2!x 1 4 1 3
12. Writing Explain the relationship between the domain of a function and the range of the function’s inverse. They are equal
13. A spherical water tank holds 6000 ft3 of water. What is the diameter of the tank p to the nearest tenth of a foot? (Hint: V 5 6 d3 ) 22.5 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
86
Name
Class
Date
Chapter 6 Test
Form K
Do you know HOW? Simplify each radical expression. Use absolute value symbols when needed. 3
1. "49x2y10 7»xy5…
5
2. " 264y9 24y3
3. " 243x15 3x3
5. "7x3 ? "14x 7x2 !2
6. 3" 4x3 ? " 8xy5
Multiply and simplify. 3
3
4. " 15 3 " 18 3
3 !10
Rationalize each denominator. Simplify your answer. !x !5x 1 !3 7. 8. 5 !3 3 !5
4
4
4
6xy !2y
3 ! 4 !2x
3
!2x2 x
9. 3
Multiply. 10. (7 1 !5)(1 1 !5) 12 1 8"5
11. (6 1 !10)2 46 1 2"10
12. (5 1 !3)(2 2 !3) 7 2 3 !3
Simplify each number. 2
3
14. 251.5 125
13. 273 9
15. 2 4
4
!8
Write each expression in simplest form. 3
16. ax2 b
22
1 x3
4
3 3
17. Q x 4 R
3 1 16 y 4
x
18. Q x 2 8y 4 R
x6
Solve. 19. !2x 1 1 5 5
x 5 12
1
3
20. (x 1 6) 4 5 8
x 5 10
21. Ax2 1 13B 2 5 7 x 5 6 and x 5 26
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
87
Name
Class
Date
Chapter 6 Test (continued)
Form K
Let f (x) 5 "x 1 3 and g (x) 5 4 2 "x. Perform each function operation and then find the domain. 22. ( f 2g) (x) (f 2 g)( x) 5 2"x 2 1;
23. ( f ? g)(x) (f ? g)( x) 5 "x 2 x 1 12; all real numbers L 0
all real numbers L 0
Let f (x) 5 3x 1 1 and g (x) 5 x2 1 2. Find each value or expression. 24. ( f + g)(2) 19
25. (g + f )(23) 66
Graph each relation and its inverse. 26. y 5 x 1 4
4 2 4 2 O 2
27. y 5 x2 2 2
y
yx4
4 2
yx4
4x
2
y
y x2 2
4 2 O 2
x 2
4
4 y 兹x 2
4
Rewrite each function to make it easy to graph using transformations of its parent function. Describe the graph. 3
28. y 5 "16x 2 32 y 5 4"x 2 2 ;
29. y 5 "8x 1 3
3
y 5 2" x 1 3; 3
vertical stretch of y 5 "x by a factor of
vertical stretch of y 5 " x by a factor of
4 and translation 2 units right
3 and translation 3 units up
Do you UNDERSTAND? 30. Error Analysis Explain the error in this simplification of radical expressions. 3 What is the correct simplification? !2 ? ! 8 5 !2(8) 5 !16 5 4
The product property does not apply to different indexes; 2 !2
6
6
31. Reasoning Show that " x3 5 !x by rewriting " x3 in exponential form. 6
"x 3 5
3 x6
5
1 x2
5 !x
32. A store is having a sale with a 15% discount on all items. In addition, employees get a
$20 discount on purchases of $100 or greater. Will an employee get a better deal if the $20 discount is applied first or if the 15% discount is applied first to their purchase of $100? The employee will pay less if the 15% discount is applied first.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
88
Name
Class
Date
Chapter 6 Performance Tasks
Give complete answers. Task 1 a. Write a product of two square roots so that the answer, when simplified
is 12x3y2. Show how your product simplifies to give the correct answer. b. Write a quotient of two cube roots so that the answer, when simplified, is
Show how your quotient simplifies to give the correct answer.
3a2 . 4b3
c. Write a product of the form Q a 1 !b R Q a 2 !b R so that the answer, when
simplified, is 59. Show how your product simplifies to give the correct answer. [4] Check students’ work. All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found products and quotient correctly but followed through the process incorrectly using incorrect simplification. [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student understood that squaring, cubing or multiplying was involved but was unable to correctly find the products or quotient, or to simplify them. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown
Task 2 a. Find a radical equation of the form !ax 1 b 5 x 1 c so that one solution is
extraneous. Show the steps in solving the equation. b. Is there a value for h that makes it possible for the equation !x 1 h 1 5 5 0
to have any real number solutions? Explain. c. Explain the relationship between the solutions to the equation
!x 2 3 2 2 5 0 and the graph of the function y 5 !x 2 3 2 2. [4] Check students’ work. All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found parts (a) and (b) correctly but could not explain (c) OR could not show steps in (a) OR could not explain (b). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student know to square each side of the equation, but could not complete the solution. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
89
Name
Class
Date
Chapter 6 Performance Tasks (continued)
Let f (x) 5 x2 1 x 2 12 and g(x) 5 x 2 2. Answer each of the following questions. Task 3 g(x)
x22 ; all real numbers a. Find f(x) and its domain. Explain how you determined the domain. 2 x 1 x 2 12 except 3 and 24 b. Find (g + f)(x) and (f + g)(x). Are they equal? x2 1 x 2 14; x2 2 3x 2 10; no
c. For what types of functions will (g + f)(x) and (f + g)(x) both equal x? Explain. when f and g are [4] All parts of Task completed correctly with work shown OR used correct inverses process with minor computational errors. [3] Student found all parts correctly but could not explain (a) OR could not explain (c) OR could not correctly find the domain for (a). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student found part (a) but could not compose functions for parts (b) and (c). [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Give complete answers. Task 4 a. Find the inverse of f(x) 5 !x 2 2 1 5. Show all steps in the process. What
is the domain of
f21 ? f 21(x) 5 (x 2 5)2 + 2; domain: x L 5
b. Choose a value for a and use the inverse to find Q f + f21 R (a) and
Q f21 + f R (a) for the value you chose. What can you conclude about Q f + f21 R (a) and Q f21 + f R (a)? (f ° f21)(a) 5 (f 21 ° f)(a) 5 a c. Graph f and
6
y
4
x O
on the same axes. What relationships do you see between the two graphs? The graphs are a reflection of each other across the line y 5 x.
[4] All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found parts (a) and (b) correctly but could not describe the relationships between the graphs OR could not draw conclusions in part (b). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student found the inverse of f(x) but could not draw conclusions in part (b) and could not graph the functions. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Prentice Hall Algebra 2 • Teaching Resources
90
f1
2
f21
Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
f
2
4
6
Name
Class
Date
Chapter 6 Cumulative Review
Multiple Choice For Exercises 1−12, choose the correct letter. 1. What is an equation for this graph? B
y 5 (x 1 3)2 1 1
y 5 (x 2 1)2 2 3
y 5 (x 2 3)2 1 1
y 5 (x 2 1)2 1 3
7 6 5 4 3 2 1
y
x
O 1 2 3 4 5 6 7
2. Simplify
3 42
. I 3 2
24 3. Solve the system. e
6
8
y 5 x2 2 3x 2 8 C y5x14
(22, 2), (2, 210)
(22, 2), (6, 10)
(21, 24), (1, 5)
(2, 6), (6, 10)
4. Which of the following polynomials has roots 0, 1, and 2? G
p(x) 5 x2 1 x 1 2
p(x) 5 x3 2 2x 1 1
p(x) 5 x3 2 3x2 1 2x
p(x) 5 x2 1 2x
5. Complete the square. 3x2 2 2x 1
1 9
uB
1 3
1
3
6. Let f(t) 5 t2 1 5t 2 2 and h(t) 5 t2 2 2t 2 6. What is the function for h(t) 1 f(t)? F
2t2 1 3t 2 8
4t2 1 t 2 8
22t2 1 3t 2 2
2t2 1 t 2 8
213 1 11i
215 2 2i
5 4 i !29 2
25 4 i !21 2
7. Simplify. (25 1 2i)(3 2 i) C
22 1 i
217 1 i
8. What is the solution to x2 2 5x 1 1 5 0? F
5 4 !21 2
25 4 !29 2
9. If h(x) 5 2x2 1 x 2 5 and g(x) 5 24x 2 1, what is the value of h(1) 2 g(3)? C -15
-11
11
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
91
15
Name
Class
Date
Chapter 6 Cumulative Review (continued)
10. Solve the system. e
y 5 2x2 1 x 1 12 G y 5 x2 1 3x
(24, 4), (0, 12)
(23, 0), (0, 12)
(23, 0), (2, 10)
(21, 22), (0, 12)
11. Which of the following relations defines y as a function of x? C
x2 1 y2 5 6 6 2 2i 12. Simplify. 1 1 3i F
22i
y 5 4 !4 2 x
y 5 x2 2 3
x 5 y2
6 2 23i
6 8 5 1 5i
6 8 5 2 5i
Short Response For Exercises 13 and 14, let f(x) 5 x2 1 2x 2 3 and g(x) 5 4x 2 1. 13. Simplify each expression. a. g(x 1 2) 4x 1 7
b. f(x 1 2) x2 1 6x 1 5 6
14. Find each value. a. (g + f )(0) 213
b. (f + g)(0) 24
2 O
y
x 6
10
2x2
y, 2 2x 1 3 15. Solve by graphing. e 2 y . x 2 x 2 12 16. To find the time t, in seconds, it takes an object to fall h meters, use the h equation t 5 Å4.9 . A croissant dropped from the top of the Eiffel Tower takes 8.13 s to reach the ground. How tall is the Eiffel Tower? 324 m
Simplify each expression. Assume that all variables are positive. 4
125a15b7 3 625a16b4 17. a b 16 28a3b4
18. Q 4 2 5 !3 R Q 4 1 5 !3 R
259
Extended Response 19. Writing Explain how you can obtain the solutions to a system of equations by graphing. 19. [4] Answers may vary. Sample: Graph both equations on the same grid. If the graphs do not intersect, then the system has no solution. If the graphs intersect in one or more points, then the intersection point(s) are the solution(s) of the system. [3] Explanation shows understanding of the concepts with some minor errors. [2] Explanation contains minor errors. [1] Explanation contains major errors and lacks detail. [0] Explanation is missing. 20. Open-Ended Write the equation of a parabola with vertex at (22, 3). 20. [4] Answers may vary. Sample: f(x) 5 (x 1 2)2 1 3. [3] Equation has minor errors. [2] Equation has major errors. [1] Equation is incomplete and the given answer has errors. [0] Equation is missing. Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
92
TEACHER INSTRUCTIONS
Chapter 6 Project Teacher Notes: Swing Time
About the Project The Chapter Project gives students an opportunity to conduct experiments involving a real-world application of physics and mathematics. Students solve a formula for a given variable to write the formula in a more useful form, then use the formula to determine the periods of pendulums.
Introducing the Project • Ask students if they have ever used a pendulum, or a swing-like motion. Remind them that the motion of a playground swing is similar to a pendulum’s motion. • Have students speculate as to whether a homemade pendulum could continue to swing forever, or if it would eventually stop swinging. Encourage them to discuss what might cause a pendulum to stop swinging.
Activity 1: Constructing Students use strings, coins, and binder clips to construct simple pendulums.
Activity 2: Investigating Students perform experiments to time the swings of their pendulums and record their observations in charts.
Activity 3: Analyzing Students solve a formula for a given variable, then use the formula to find the theoretical periods of their pendulums. They analyze their data and determine why their experimental results might differ from their theoretical results.
Finishing the Project You may wish to plan a project day on which students share their completed projects. Encourage students to explain their processes as well as their results. • Have students review their data and their calculations of the periods. • Ask groups to share their insights that resulted from completing the project, such as any shortcuts they found for using the formula or calculating the periods. SOURCES: Basic Physics: A Self-Teaching Guide, Second edition, p. 104, by Karl F. Kahn, 1996, John Wiley & Sons, Inc.; Physics, p. 242, by John D. Cutnell and Kenneth W. Johnson, 1989, John Wiley & Sons, Inc.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
93
Name
Class
Date
Chapter 6 Project: Swing Time
Beginning the Chapter Project Galileo observed a swinging lantern and made an important discovery about the timing of a pendulum’s swing. A Dutch man named Christiaan Huygens discovered the relationship between the length of a pendulum and the time it takes to make a complete swing, which led to the use of pendulums in clock making. You will construct pendulums using strings and weights and use your pendulums to investigate whether the length of the string or the amount of weight attached to a pendulum affects the time it takes the pendulum to make one full swing.
List of Materials • Calculator
• Metric ruler or measuring tape
• Thread or thin string
• Binder clips (2 medium)
• Coins (3 quarters, 3 nickels, or 3 pennies)
• Stopwatch
Activities Activity 1: Constructing To construct a simple pendulum, tie a medium binder clip to the end of a piece of string. The binder clip will be used to hold one or more coins for the experiments in Activity 2. The weight on the end of the string, which includes the binder clip and the coin(s) it holds, is called the pendulum bob. The period of a pendulum is the time it takes for the pendulum to complete one full swing (back and forth). Activity 2: Investigating Experiment 1 Tie the free end of the string of the pendulum to a stable object. Do this in such a way that neither the string nor the bob touch another object when the pendulum is swung. Insert one coin in the binder clip. Measure the length of the string (in centimeters) from the point where it is attached to the stable object to the center of the bob. Record this length. Three times, pull the pendulum back to an angle of about 20° and let it go. For each trial, use a stopwatch to record the number of seconds it takes for the pendulum to complete 10 full swings. Record each time in the first column of the table provided on the next page. Next, find and record the average of the three times you listed. Finally, divide the average time by 10 to determine the period of the pendulum. Repeat the procedure using two coins, then using three coins, recording the data in the second and third columns, respectively. Does it appear that the weight of the bob affected the period of the pendulum? What factors other than the weight might affect the period of the pendulum? Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
94
Name
Class
Date
Chapter 6 Project: Swing Time (continued)
1 coin
2 coins
3 coins
Trial 1 Trial 2 Trial 3 Average time to complete 10 full swings Period of pendulum
Experiment 2 Cut a second string that is half the length of the original string. Repeat Experiment 1. Record data in a table. Does it appear that the pendulum string length affects its period? Explain. Activity 3: Analyzing 2
The formula / 5 980t2 represents the length O (in centimeters) of a simple 4p pendulum with a period of t seconds. (In this formula, the acceleration due to gravity is given as 980 cm/s2.) • Solve for t. According to the formula, how does changing the weight of the bob affect the period of a pendulum? • Use the formula to find the theoretical period for each pendulum. Record your experimental and theoretical periods for each. Length of Pendulum
Experimental Period
Theoretical Period
Experiment 1 Experiment 2
Do your experimental results give the same period as the theretical models? What factors do you think would for any differences? Explain your observations.
Finishing the Project Prepare a presentation for the class describing your results. Your presentation should include a chart showing your experimental and theoretical results.
Reflect and Revise When you are sure your data are accurate, decide if your presentation is complete, clear, and convincing. If needed, make changes to improve your presentation.
Extending the Project Research the use of clock pendulums. Find out how a pendulum keeps time. Research periods of the pendulums used in different clock types. Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
95
Name
Class
Date
Chapter 6 Project Manager: Swing Time
Getting Started Read the project. As you work on the project, you will need a calculator and materials on which you can record your results and make calculations. Keep all of your work for the project in a folder, along with this Project Manager. Checklist
Suggestions
☐ Activity 1: constructing a pendulum
☐ Use the lightest thread or string possible.
☐ Activity 2: determining the period
☐ Have one student swing the pendulum while another student keeps time.
☐ Activity 3: comparing experimental and theoretical periods
☐ Isolate t, then take the square root of each side of the equation. Substitute the string lengths into the new equation.
☐ pendulum experiment
☐ How would your results change if your pendulum were not able to swing freely, that is without with any other object? How would your results change if you pulled the pendulum back to an angle of 60°? What other changes would affect your results?
Scoring Rubric 4
Your experimental results are reasonable. Calculations are correct. Explanations are thorough and well thought out. Data, calculations, and conclusions are neatly presented.
3
Your experimental results are reasonable. Calculations are mostly correct with some minor errors. Explanations lack detail and accuracy. Data, calculations, and conclusions are not well organized.
2
Your experimental results are not reasonable. Calculations and explanations contain errors. Data, calculations, and conclusions are unorganized and lack detail.
1
Major concepts are misunderstood. Project satisfies few of the requirements and shows poor organization and effort.
0
Major elements of the project are incomplete or missing.
Your Evaluation of Project Evaluate your work, based on the Scoring Rubric.
Teacher’s Evaluation of Project Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
96
Class
Date
Additional Vocabulary
6-1
Roots and Radical Expressions
Complete the vocabulary chart by filling in the missing information. Word or Word Phrase
Definition
Example
nth root
Given the equation an 5 b, a is the nth root of b.
1. 34 5 81; 3 is the 4th root of 81.
radicand
2. The number under the radical sign.
The radicand in the expression 3 ! 64 is 64.
index
The number that gives the degree of the root.
3. The index in the
cube root
The third root of a number.
4. The cube root of 8 is 2.
principal root
5. The positive root when a number has both a positive and a negative root.
The principal square root of 4 is 2.
5
expression !32 is 5.
Choose the word or phrase from the list that best completes each sentence. cube root 6. The
nth root
radicand
radicand
index
principal root
is the number under the radical sign in a radical
expression. 7. The
cube root
of 27 is 3.
8. Given the equation an 5 b, a is the 9. In a radical expression, the
nth root
index
of b.
indicates the degree of
the root. 10. When a number has both a positive and a negative root, the positive root is
considered the
principal root
.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
1
Name
6-1
Class
Date
Think About a Plan Roots and Radical Expressions
Boat Building Boat builders share an old rule of thumb for sailboats. The maximum speed K in knots is 1.35 times the square root of the length L in feet of the boat’s waterline. a. A customer is planning to order a sailboat with a maximum speed of 12 knots. How long should the waterline be? b. How much longer would the waterline have to be to achieve a maximum speed of 15 knots? 1. Write an equation to relate the maximum speed K in knots to the length L in feet of a boat’s waterline. K 5 1.35!L
2. How can you find the length of a sailboat’s waterline if you know its maximum
speed? Substitute the maximum speed for K and solve the resulting equation for L
.
3. A customer is planning to order a sailboat with a maximum speed of 12 knots. How long should the waterline be? about 79 ft
4. How can you find how much longer the waterline would have to be to achieve
a maximum speed of 15 knots, compared to a maximum speed of 12 knots? Subtract the waterline length needed for a 12-knot maximum speed from the waterline length needed for a 15-knot maximum speed
5. If a customer wants a sailboat with a maximum speed of 15 knots, how long should the waterline be? about 123 ft
6. How much longer would the waterline have to be to achieve a maximum speed of 15 knots? about 44 ft
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
2
.
Name
Class
Date
Practice
6-1
Form G
Roots and Radical Expressions
Find all the real square roots of each number. 1. 400 220, 20
2. 2196 no real 3. 10,000 2100, 100 square roots
4. 0.0625 20.25, 0.25
Find all the real cube roots of each number. 5. 216 6
6. 2343 27
1000 8. 27 10 3
7. 20.064 20.4
Find all the real fourth roots of each number. 9. 281 no real fourth roots
12. 625 25, 5
10. 256 24, 4
11. 0.0001 20.1, 0.1
14. 2!25 25
15. !20.01 not a real 16. !0.001 0.1 number
Find each real root. 13. !144 12 4
17. !0.0081 0.3
3
3
3
18. !27 3
19. !227 23
20. !0.09 0.3
Simplify each radical expression. Use absolute value symbols when needed. 21. "81x4 9x2
22. "121y10 11 »y5…
3
5
3
23. " 8g6 2g2
3
24. " 125x9 5x3
25. " 243x5y15 3xy3
26. " (x 2 9)3
27. "25(x 1 2)4 5(x 1 2)2
3 3 64x9 28. %343 4x7
29. !20.008
31. "36x2y6 6»x…y3
4 32. " (m 2 n)4 »m 2 n…
4 x4
30. % 81
»x… 3
3
x29
20.2
33. A cube has volume V 5 s3 , where s is the length of a side. Find the side length for a cube with volume 8000 cm3. 20 cm
34. The temperature T in degrees Celsius (8C) of a liquid t minutes after heating is given by the formula T 5 8 !t . When is the temperature 488C? 36 min
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
3
Name
6-1
Class
Date
Practice (continued)
Form G
Roots and Radical Expressions
Find the two real solutions of each equation. 35. x2 5 4 22, 2
36. x4 5 81 23, 3
37. x2 5 0.16 20.4, 0.4
4 4 16 38. x2 5 49 27, 7
2 2 16 39. x4 5 625 25, 5
121 11 11 40. x2 5 625 225, 25
41. x2 5 0.000009 20.003, 0.003
42. x4 5 0.0001 20.1, 0.1
43. The number of new customers n that visit a dry cleaning shop in one year
is directly related to the amount a (in dollars) spent on advertising. This relationship is represented by n3 5 13,824a. To attract 480 new customers, how much should the owners spend on advertising during the year? $8000 44. Geometry The volume V of a sphere with radius r is given by the formula
V 5 43 pr3 . a. What is the radius of a sphere with volume 36p cubic inches? 3 in. b. If the volume increases by a factor of 8, what is the new radius? 6 in.
45. A clothing manufacturer finds the number of defective blouses d is a function
of the total number of blouses n produced at her factory. This function is d 5 0.000005n2 . a. What is the total number of blouses produced if 45 are defective? 3000 b. If the number of defective blouses increases by a factor of 9, how does the total number of blouses change? It has tripled. 46. The velocity of a falling object can be found using the formula v2 5 64h,
where v is the velocity (in feet per second) and h is the distance the object has already fallen. a. What is the velocity of the object after a 10-foot fall? about 25.30 ft/sec b. How much does the velocity increase if the object falls 20 feet rather than 10 feet? about 10.48 ft/sec
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
4
Name
6-1
Class
Date
Practice
Form K
Roots and Radical Expressions
Find all the real square roots of each number. 1. 625 625
2. 21.44 no real roots
16 3. 81 6 49
Find all the real cube roots of each number. 1 5. 64
4. 2216 26
6. 0.027 0.3
1 4
Find all the real fourth roots of each number. 7. 0.2401 60.7
8. 1 61
9. 21296 no real fourth roots
Find each real root. To start, find a number whose square, cube, or fourth is equal to the radicand. 4
10. !400
3
12. !2729 29
11. 2!256 24
5 "(20)2 20
Simplify each radical expression. Use absolute value symbols when needed. To start, write the factors of the radicand as perfect squares, cubes, or fourths. 3
13. "25x6
5 "(5)2(x3)2 5»x 3…
14. " 343x9y12 7x 3y 4
4
15. " 16x16y20 2x 4»y 5…
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
5
Name
6-1
Class
Date
Practice (continued)
Form K
Roots and Radical Expressions
4 16. The formula for the volume of a sphere is V 5 3 pr3 . Solving for r, the radius of 3 3V a sphere is r 5 Å 4p . If the volume of a sphere is 20 ft3, what is the radius of the sphere to the nearest hundredth? 1.68 ft
Find the two real solutions of each equation. 17. x4 5 81 63
2401 19. x4 5 625 w 75
18. x2 5 144 6 12
20. Writing Explain how you know whether or not to include the absolute value
symbol on your root. If the index is odd, then you do not use the absolute value symbol on your root. If the index is even, then you need the absolute value symbol on those variable with an odd power. 3
3
6
21. Arrange the numbers !264, 2!264, !64, and !64, in order from least to 3 3 6 , !64, 2 !264 , !64 greatest. !264
22. Open-Ended Write a radical that has no real values. Answers may vary. Sample: any even index radical with a negative radicand
23. Reasoning There are no real nth roots of a number b. What can you conclude
about the index n and the number b? The index n is even and the number b is negative.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
6
Name
Class
6-1
Date
Standardized Test Prep Roots and Radical Expressions
Multiple Choice For Exercises 1−6, choose the correct letter. 1. What is the real square root of 0.0064? B
0.4
0.04
0.08
no real square root
2. What is the real cube root of 264? G
4
28
24
no real cube root
16 3. What is the real fourth root of 281 ? D 2 3
249
223
no real fourth root 3
4. What is the value of !20.027? F
20.3
0.3
20.03
0.03
5. What is the simplified form of the expression "4x2y4 ? B
2xy2
2 u x uy2
4xy2
2 u xy u
6. What are the real solutions of the equation x4 5 81? H
29, 9
3
23, 3
23
Short Response 7. The volume V of a cube with side length s is V 5 s3. A cubical storage bin has
volume 5832 cubic inches. What is the length of the side of the cube? Show your work. 3
[2] V 5 s3, 5832 5 s3, s 5 !5832 5 18; 18 in. [1] incorrect side length OR no work shown [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
7
Name
Class
6-1
Date
Enrichment Roots and Radical Expressions
Rounding Roots and Radicals Computers treat radicals such as !2 as if they were rounded to a preassigned number of decimal places. Most computers round numbers according to an algorithm that uses the largest integer less than or equal to a given number. This function is called the greatest integer function and is written as y 5 fxg. As you can see, the graph of the greatest integer function is not continuous. The open circles indicate that the endpoint is not included as part of the graph. The command INT in most popular spreadsheet programs serves the same purpose as the greatest integer function. For instance, INT(3.84) 5 3; INT(21.99) 5 22; INT(7) 5 7. To round a number x to r decimal places, a computer performs the following procedure: y
Step 1
Multiply x by 10r.
Step 2
Add 0.5 to the result.
Step 3
Find INT of the result.
Step 4
Multiply the result by 102r.
2 x ⫺2
O
2
Fill in the table below to see how this procedure works. x
r
Step 1
Step 2
Step 3
Step 4
11.4825
3
11482.5
11483
11483
11.483
132.718
2
13271.8
13272.3
13272
132.72
34.999
1
349.99
350.49
350
35.0
A computer that rounds numbers after each operation may introduce rounding errors into calculations. To see the effects of rounding errors, perform each of the following computations for x 5 2 and different r values. First find the given root and write the answer to r 1 1 digits after the decimal. Carry out the four steps to get the answer and then raise the result to the given power. Write the answer again to r 1 1 digits after the decimal and carry out the four steps to get the final answer. 2
3
Q !x R
3
x
r
Q !x R
2
6
2.000001
2.000000
2
3
1.999
2.000
2
1
2.0
2.2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
8
Name
Class
6-1
Date
Reteaching Roots and Radical Expressions
For any real numbers a and b and any positive integer n, if a raised to the nth power equals b, then a is an nth root of b. Use the radical sign to write a root. The following expressions are equivalent: index
power an 5 b
g
radicand n
!b ! b5a
radical sign Problem
What are the real-number roots of each radical expression? 3
a. !343
b.
4 1 Å625
3
Because (7)3 5 343, 7 is a third (cube) root of 343. 3 Therefore, !343 5 7. (Notice that (27)3 5 2343, so 27 is not a cube root of 343.)
1 1 1 Because Q 15 R 4 5 625 and Q 215 R 4 5 625 , both 15 and 215 are real-number fourth roots of 625 .
c. !20.064
Because (20.4)3 5 20.064,20.4 is a cube root of 20.064 and is, in fact, the only one. 3 So, !20.064 5 20.4.
d. !225
Because (5)2 5 (25)2 5 25, neither 5 nor 25 are second (square) roots of 225. There are no real-number square roots of 225.
Exercises Find the real-number roots of each radical expression. 3
1. !169 213, 13 4. 7.
3
4
2. !729 9
218 212
5.
4 225 no real sq root
8. !0.1296 20.6, 0.6
Å
Å
4
10. !20.0001 no real 4th root
4
3. !0.0016 20.2, 0.2
Å121
2 2 211 , 11
4
11.
5 1 1 Å 243 3
6.
3 125 5 Å 216 6
3
9. !20.343 20.7 12.
3 8 Å 125
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
9
2 5
Name
Class
6-1
Date
Reteaching (continued) Roots and Radical Expressions n
You cannot assume that "an 5 a. For example, "(26)2 5 !36 5 6, not 26. This leads to the following property for any real number a: n
If n is odd
"an 5 a
If n is even
"an 5 u a u
n
Problem
What is the simplified form of each radical expression? 3
a. " 1000x3y9 3 3 " 1000x3y9 5 " 103x3(y3)3
Write each factor as a cube.
3 5" (10xy3)3
Write as the cube of a product.
5 10xy3
Simplify.
8
256g b. 4 4 16 Åh k
4
256g8
Å h4k16
5
4
44(g2)4
Å h4(k4)4
Write each factor as a power of 4.
2 4
4g 5 4 a 4b Å hk 5
4g2 u hu k4
Write as the fourth power of a quotient. Simplify.
The absolute value symbols are needed to ensure the root is positive when h is negative. Note that 4g2 and k4 are never negative.
Exercises Simplify each radical expression. Use absolute value symbols when needed. 3
13. "36x2 6»x… 16.
"x20 "y8
14. " 216y3 6y (x 1 3)3 17. 3 Å (x 2 4)6
x10 y4
27z3 19. 3 Å (z 1 12)6 (y 2 4)8 22. 4 Å (z 1 9)4
3z (z 1 12)2 (y 2 4)2 »z 1 9…
15. x 1 3 (x 2 4)2
4 20. " 2401x12 7»x3… 6 6
a b 23. 3 3 Å c
a 2b 2 c
1 Å 100x2
5 18. " x10y15z5 x2y3z
1331 21. 3 Å x3
11 x
3 24. " 2x3y6 2xy2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
10
1 10»x…
Name
Class
Date
Additional Vocabulary
6-2
Multiplying and Dividing Radical Expressions
Combining Radicals: Products n
n
n
n
n
If !a and !b are real numbers, then !a ? !b 5 !ab. Sample
3 3 3 3 !8 ? !27 5 !8 ? 27 5 !216 5 6
Solve. 3
3
1. !16 ? !4 5
3
3
!16 ? 4 5 !64 5 4
2. Which of the following products can be simplified? Circle the correct answer. 3 ! 12 ? !6
4 4 ! 16 ? ! 24
4 3 ! 35 ? ! 10
3
3. Write the radical expression !32x 4 in simplest form.
3 2x !4x
4. Which of the following products cannot be simplified? Circle the correct answer. 4 4 ! 15 ? ! 4
4 3 ! 10 ? ! 5
!4 ? !12
5. "4x2y3 ? "27x2y2 5
6x2y2"3y
Combining Radicals: Quotients n
n
n
If !a and !b are real numbers and b 2 0, then Sample
!8 5 !2
8 Å2
!a a 5 nÅb . n !b
5 !4 5 2
Solve. 6. Which of the following quotients can be simplified? Circle the correct answer. 3
3
!12
4
!6
3 !4
!20 3 !15
"3
"64x4 l4xl in simplest form. "4x2 8. Rewriting an expression so that there are no radicals in any denominator and no rationalizing the denominator denominators in any radical is called . 7. Write the radical expression
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
11
Name
6-2
Class
Date
Think About a Plan Multiplying and Dividing Radical Expressions
Satellites The circular velocity v, in miles per hour of a satellite orbiting Earth is 12
given by the formula v 5 Å1.24 3r 10 , where r is the distance in miles from the satellite to the center of the Earth. How much greater is the velocity of a satellite orbiting at an altitude of 100 mi than the velocity of a satellite orbiting at an altitude of 200 mi? (The radius of the Earth is 3950 mi.) Know
z
z
mi . 1. The first satellite orbits at an altitude of 100
z
z
mi . 2. The second satellite orbits at an altitude of 200
z
z
mi . 3. The distance from the surface of the Earth to its center is 3950
Need 4. To solve the problem I need to find: the difference in the velocities of a satellite orbiting at an altitude of 100 mi and one orbiting at an altitude of 200 mi
Plan 5. Rewrite the formula for the circular velocity of a satellite using a for the
altitude of the satellite. v 5 1.24 3 1012 Å a 1 3950 6. Use your formula to find the velocity of a satellite orbiting at an altitude of 100 mi. about 17,498 mi/h 7. Use your formula to find the velocity of a satellite orbiting at an altitude of 200 mi. about 17,286 mi/h 8. How much greater is the velocity of a satellite orbiting at an altitude of 100 mi than one orbiting at an altitude of 200 mi? about 212 mi/h
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
12
.
Name
Class
Date
Practice
6-2
Form G
Multiplying and Dividing Radical Expressions
Multiply, if possible. Then simplify. 1. !4 ? !25 10 3
3
4. " 45 ? " 75 15
3
2. !81 ? !36 54
3. !3 ? !27 9
5. !18 ? !50 30
6. !216 ? !4 24
3
3
Simplify. Assume that all variables are positive. 7. "36x3 6x !x
3 3 8. " 125y2z4 5z"y2z
3
3
10. " 216a12 22a4 !2 3
3 13. " 216x4y3 6xy "x
9. "18k6 3k3"2 4
4
11. "x2y10z xy5"z
12. " 256s7t12 4st3 "s3
14. "75r3 5r"3r
4 4 15. " 625u5v8 5uv2 !u
Multiply and simplify. Assume that all variables are positive. 3
16. !4 ? !6 2 "6
2 17. "9x2 ? "9y5 9xy !y
3 3 2 2 18. " 50x2z5 ? " 15y3z 5yz "6x
19. 4 !2x ? 3 !8x 48x
20. !xy ? !4xy 2xy
21. 9 !2 ? 3 !y 27 !2y
22. "12x2y ? " 3xy4
23. "29x2y4 ? " 12xy
24. 7"3y2 ? 2"6x3y
3
42xy"2xy
3
3
23xy "4y2
6xy2"xy
Divide and simplify. Assume that all variables are positive. 25.
"75 5 "3
26.
28.
"6x "2 "3x
29.
"(2x)2
2x 31. "(5y)4 25y2
"63xy3 "7y
3y !x
3
"4x2 3 "4x 3 "x 3
3 "18y2 " 12y 32. 3 2 "12y
27.
"54x5y3 3xy !3x "2x2y
3 4 243k 3 30. Ä 7
3k
162a
33. Ä 3 6a
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
13
k
3"3 a
Name
Class
6-2
Date
Practice (continued)
Form G
Multiplying and Dividing Radical Expressions
Rationalize the denominator of each expression. Assume that all variables are positive. 34.
!y "5y !5
35.
5
37.
9x 3"2x 2 2
38.
Å
"18x2y "2y3
41.
"4x2
!xy "3y !3x 3
4
!2x 4 "54x3 40. 4 "3x2 3x
3
"7xy2
36. 3
3x y
3 2 2 3 x2 " 9x y 39. Ä 3y 3y
x "2xy
Å8y
3
"14x2y2 2x
3 3a 42. Ä 2
3
"6abc2 4b c 2bc
4y
43. What is the area of a rectangle with length !175 in. and width !63 in.? 105 in.2 44. The area of a rectangle is 30 m2. If the length is !75 m, what is the width? 2"3 m
1 45. The volume of a right circular cone is V 5 3pr2h, where r is the radius of the base and h is the height of the cone. Solve the formula for r. Rationalize the denominator. r 5 "3πhV πh 4 46. The volume of a sphere of radius r isV 5 3pr3 . 3 3 "6π2V a. Use the formula to find r in of V. Rationalize the denominator. r 5 "3V; r 5 2π 4π b. Use your answer to part (a) to find the radius of a sphere with volume 100 cubic inches. Round to the nearest hundredth. 2.88 in.
Simplify each expression. Rationalize all denominators. Assume that all variables are positive. 47. !14 ? !21 7"6 50.
6 !2x 2"6x 5 5 !3
3
3
3
48. !150 ? !20 10 "3
8 3 4 "4x 2 x "2x
51. 3
49. !3 Q !12 2 !6 R 6 2 3"2 3
5 !xy4 3 2 52. 3 "5y "25xy2
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
14
Name
Class
Date
Practice
6-2
Form K
Multiplying and Dividing Radical Expressions
Multiply, if possible. Then simplify. To start, identify the index of each radical. 3
3
1. !4 ? !6
index of both radicals is 3
3
2. !5 ? !8 2 !10
4
3. !6 ? !9 The indexes are different, so you cannot multiply.
3 !4 ? 6 2 !3 3
Simplify. Assume all variables are positive. To start, change the radicand to factors with the necessary exponent. 3
4. " 27x6 3 3 5" 3 ? (x2)3 3x 2
5
5. "48x3y4 4xy 2 !3x
6. " 128x2y25 5
2y 5 "4x 2
Multiply and simplify. Assume all variables are positive. 4
4
3
8. " 7x6 ? " 32x2
7. !12 ? !3 6
3
9. 2" 6x4y ? 3" 9x5y2
4
3 18x 3y !2
2x 2 !14
Simplify each expression. Assume all variables are positive. 3
3
3 10. !4 ? !80 4 !5
11. 5"2xy6 ? 2"2x3y 20x 2y 3 !y
12. !5 Q !5 1 !15 R 5 1 5 !3
3
13. Error Analysis Your classmate simplified "5x3 ? " 5xy2 to 5x2y. What mistake did she make? What is the correct answer? She thought the indexes were the same. They are different, so you cannot multiply the radicands.
3 3 14. A square rug has sides measuring ! 16 ft by ! 16 ft. What is the area of the rug? 3 2 4 !4 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
15
Name
Class
6-2
Date
Practice (continued)
Form K
Multiplying and Dividing Radical Expressions
Divide and simplify. Assume all variables are positive. To start, write the quotient of roots as a root of a quotient. 15.
4
"36x6 "9x4
16.
"405x8y2 4
"5x3y2
3
17.
4
6 5 Å36x4 2x
3
"25x4 3
3x !x
9x
"75x7y2 x "3y 2
Rationalize the denominator of each quotient. Assume all variables are positive. To start, multiply the numerator and denominator by the appropriate radical expression to eliminate the radical. 3 "7x4y !26 ! x 18.
19. 3 !2
!3
5
20.
!26 !3 !78 ? !3 !3 3
!5xy
x !35x 5
3
!4x 2
21. Einstein’s famous formula E 5 mc2 relates energy E, mass m, and the speed of
light c. Solve the formula for c. Rationalize the denominator. !Em
E c 5 Åm ;c5 m
22. The formula h 5 16t2 is used to measure the time t it takes for an object to free fall from
height h. If an object falls from a height of h 5 18a5 ft, how long did it take for the object 2 to fall in of a? 3a !2a seconds 4
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
16
Name
Class
6-2
Date
Standardized Test Prep Multiplying and Dividing Radical Expressions
Multiple Choice For Exercises 1−5, choose the correct letter. Assume that all variables are positive. 3 3 1. What is the simplest form of ! 249x ? " 7x2 ?
7x !7x
B
27x
7x
3 2 27" x
4"5x7y6
4x3y3 !5x
3 15xy! y
5xy !15x
5x !x 2y
5x2y 2
2. What is the simplest form of "80x7y6 ? I
2x3y3 !20x
4x6y6"5x3 3
3
3. What is the simplest form of " 25xy2 ? " 15x2 ? A 3 5x" 3y2
3 5x ! 3y
4. What is the simplest form of
5"3x4 2"3y2
"75x5 ? G "12xy2
5x2 2y 3
2"x2y 5. What is the simplest form of 3 ? C "4xy2 3
"x2y 2y
3
3
"2xy2 y
x !2y y
3
!2y xy
Short Response 6. The volume V of a wooden beam is V 5 ls2, where l is the length of the beam
and s is the length of one side of its square cross section. If the volume of the beam is 1200 in.3 and its length is 96 in., what is the side length? Show your work. [2] V 5 ls2; s 5 ÅVl 5 Å1200 96 5 !12.5 N 3.5 in. [1] appropriate methods but with computational errors OR correct answer without work shown [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
17
Name
6-2
Class
Date
Enrichment Multiplying and Dividing Radical Expressions n
To simplify the radical !a, you look for a perfect nth power among the factors of the radicand a. When this factor is not obvious, it is helpful to factor the number into primes. Prime numbers are important in many aspects of mathematics. Several mathematicians throughout history have unsuccessfully tried to find a pattern that would generate the nth prime number. Other mathematicians have offered conjectures about primes that remain unresolved. 1. Goldbach’s Conjecture states that every even number n . 2 can be written as
the sum of two primes. For example, 4 5 2 1 2 and 10 5 3 1 7. Choose three even numbers larger than 50 and write them as a sum of two primes. Answers may vary. Sample: 52 5 47 1 5. 2. The Odd Goldbach’s Conjecture states that every odd number n . 5 can be
written as the sum of three primes. For example, 7 5 2 1 2 1 3. Choose three odd numbers larger than 50 and write them as the sum of three primes. Answers may vary. Sample: 51 5 37 1 11 1 3. 3. Another interesting pattern emerges when you examine a subset of the prime
numbers. Make a list of the primes less than 50. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 4. Make this list smaller by eliminating 2 and all primes that are 1 less than a
multiple of 4. 5, 13, 17, 29, 37, 41 5. The remaining primes in the list above are related in an interesting way. You
can write each prime as the sum of two squares. Express each of these primes as a sum of two squares. 5 5 1 1 4, 13 5 4 1 9, 17 5 1 1 16, 29 5 4 1 25, 37 5 1 1 36, 41 5 16 1 25 6. A Cullen number, named after an Irish mathematician James Cullen, is a
natural number of the form n 3 2n 1 1. Determine the first four Cullen numbers. That is, let n 5 1, 2, 3, 4. 3, 9, 25, 65 7. What is the smallest Cullen number that is a prime number? (The next Cullen
number that is a prime occurs when n 5 141!) 3 when n 5 1 8. A palindrome is a number that reads the same forward and backward. For
example, 121 is a palindromic number. List the seven palindromic primes that are less than 140. 2, 3, 5, 7, 11, 101, 131
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
18
Name
Class
6-2
Date
Reteaching Multiplying and Dividing Radical Expressions
You can simplify a radical if the radicand has a factor that is a perfect nth power and n is the index of the radical. For example: n
n
!xynz 5 y !xz Problem
What is the simplest form of each product? 3 3 a. ! 12 ? ! 10 n
n n Use !a ? !b 5 !ab.
3 3 3 ! 12 ? ! 10 5 ! 12 ? 10 3 5 "22 ? 3 ? 2 ? 5
Write as a product of factors.
3 3 5" 2 ?3?5
Find perfect third powers.
3 3 5 "23 ? "3 ? 5
n Use !ab 5 !a ? !b.
3 5 2! 15
Use "an 5 a to simplify.
n
n
n
b. "7xy3 ? "21xy2 n n n Use !a ? !b 5 !ab.
"7xy3 ? "21xy2 5 "7xy3 ? 21xy2 5 "7xy2y ? 3 ? 7xy2
Write as a product of factors.
5 "72x2(y2)2 ? 3y
Find perfect second powers.
5 7xy2"3y
Use !an 5 a to simplify.
n
Exercises Simplify each product. 3
3
1. !15x ? !35x 5x"21
2. " 50y2 ? " 20y 10y
4. 5"7x3y ? "28y2
5. 2" 9x5y2 ? " 2x2y5
70xy"xy
3
3
3 2x2y2 !18xy
3
6. !3 Q !12 2 !21 R 6 2 3"7
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
19
3
3
3. " 36x2y5 ? " 26x2y 26xy2 !x
Name
Class
Date
Reteaching (continued)
6-2
Multiplying and Dividing Radical Expressions
Rationalizing the denominator means that you are rewriting the expression so that no radicals appear in the denominator and there are no fractions inside the radical. Problem
What is the simplest form of
!9y !2x
?
Rationalize the denominator and simplify. Assume that all variables are positive. !9y !2x
5
9y Å 2x
Rewrite as a square root of a fraction.
5
9y ? 2x Å 2x ? 2x
Make the denominator a perfect square.
5
18xy Å 4x2
Simplify.
5
!18xy
Write the denominator as a product of perfect squares.
"22 ? x2
5
"18xy 2x
Simplify the denominator.
5
"32 ? 2 ? x ? y 2x
Simplify the numerator.
5
3"2xy 2x
Use !an 5 a to simplify.
n
Exercises Rationalize the denominator of each expression. Assume that all variables are positive. 3
"6ab2 8. 3 "2a4b
!5 "5x 7. x !x 3
11.
4"k9 3
16"k5
3
k "k 4
12.
4
4 "9y " 9x3y 9. 4 x "x
3
"3b a
4
"10 13. 4 "z2
3x5 x2"15xy Ä 5y 5y
4
"10z2 z
10.
3 19a2b " 19ac2 14. 3 4 c2 Ä abc
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
20
"10xy3 "30xy 6 "12y2
Name
6-3
Class
Date
Additional Vocabulary Binomial Radical Expressions
The column on the left shows the steps used to rationalize a denominator. Use the column on the left to answer each question in the column on the right. Problem
1. What does it mean to rationalize a
Rationalizing the Denominator
Write the expression
4 !3 !7 1 !3
denominator? Sample answer: It means to write
with a
an expression so that there are no
rationalized denominator.
radicals in any denominators and no denominators in any radicals. Multiply the numerator and the denominator by the conjugate of the denominator. 4 !3 !7 2 !3 ? !7 1 !3 !7 2 !3
2. What are conjugates? Conjugates are expressions that differ only in the signs of the first or second .
The radicals in the denominator cancel out. 4 !3A !7 2 !3B 723
3. Write and solve an equation to show
why the radicals in the denominator cancel out. (!7 1 !3)(!7 2 !3) 5 (!7 ? !7) 2 (!7 ? !3) 1 (!7 ? !3) 2 (!3 ? !3) 5 7 2 3
Distribute !3 in the numerator. 4( !3 ? !7 2 !3 ? !3) 723
4. What property allows you to distribute
Simplify. 4( !21 2 3) 4
5. Why do the fours in the numerator
the !3? The Distributive Property
and the denominator cancel out? Sample answer: Because 4 divided by 4 equals 1. 6. What number multiplied by !21
Simplify. !21 2 3
would produce a product of 21? !21
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
21
Name
Class
6-3
Date
Think About a Plan Binomial Radical Expressions
Geometry Show that the right triangle with legs of length !2 2 1 and !2 1 1 is similar to the right triangle with legs of length 6 2 !32 and 2. Understanding the Problem 1. What is the length of the shortest leg of the first triangle? Explain. !2 2 1 ; because !2 5 !2, !2 2 1 must be less than !2 1 1
2. What is the length of the shortest leg of the second triangle? Explain. 6 2 !32; because !32 is between 5 and 6, 6 2 !32 must be between 0 and 1, which is less than 2.
3. Which legs in the two triangles are corresponding legs? The smaller leg in the first triangle corresponds to the smaller leg in the second triangle. The larger leg in the first triangle corresponds to the larger leg in the second triangle.
Planning the Solution 4. Write a proportion that can be used to show that the two triangles are similar. !2 2 1 0 6 2 !32 !2 1 1
Getting an Answer 5. Simplify your proportion to show that the two triangles are similar. !2 2 1 !2 1 1
0 6 2 2!32
2(!2 2 1) 0 (!2 1 1)(6 2 !32) 2 !2 2 2 0 6 !2 2 !64 1 6 2 !32 2 !2 2 2 0 6 !2 2 8 1 6 2 4 !2 2 !2 2 2 5 2 !2 2 2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
22
2
Name
Class
Date
Practice
6-3
Form G
Binomial Radical Expressions
Add or subtract if possible. 1. 9 !3 1 2 !3
2. 5 !2 1 2 !3
11 !3
5 !2 1 2 !3
3
3
3
3
3 !7 2 7 !x
3
6. 5 !xy 1 !xy 3 6 !xy
3
9. 7 !x 1 x !7
4. 14 !xy 2 3 !xy 3 11 !xy
5. 8 !x 1 2 !y 3 3 8 !x 1 2 !y
7. !3x 2 2 !3x
8. 6 !2 2 5 !2 3
6 !2 2 5 !2
2!3x
3
3. 3 !7 2 7!x
3
3
7 !x 1 x !7
Simplify. 10. 3 !32 1 2 !50 22 !2 4
4
13. 2 !48 1 3 !243 4
13 !3
3
3
3
12. !81 2 3 !3 0
14. 3 !75 1 2 !12 19 !3
15. !250 2 !54
4
16. !28 2 !63 2!7
3
11. !200 2 !72 4 !2
4
3
2 !2
17. 3 !32 2 2 !162 0
18. !125 2 2 !20 !5
20. A1 1 4 !10B A2 2 !10B
21. A1 2 3 !7B A4 2 3 !7B
Multiply. 19. A1 2 !5B A2 2 !5B
238 1 7"10
7 2 3 !5 22. (4 2 2 !3)2
23. (!2 1 !7)2
24. A2 !3 2 3 !2B 2
9 1 2 !14
30 2 12 !6
28 2 16 !3 25. A4 2 !3B A2 1 !3B 5 1 2 !3
67 2 15 !7
26. A3 1 !11B A4 2 !11B 1 1 !11
27. A3 !2 2 2 !3B 2 30 2 12 !6
Multiply each pair of conjugates. 28. (3 !2 2 9)(3 !2 1 9) 263
29. (1 2 !7)(1 1 !7) 26
30. (5 !3 1 !2)(5 !3 2 !2) 73
31. (3 !2 2 2 !3)(3 !2 1 2 !3) 6
32. (!11 1 5)(!11 2 5) 214
33. (2 !7 1 3 !3)(2 !7 2 3 !3) 1
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
23
Name
Class
6-3
Date
Practice (continued)
Form G
Binomial Radical Expressions
Rationalize each denominator. Simplify the answer. 34.
3 2 !10 !5 2 2 !2 3 !5 2 !2
35.
3
2 1 !14 !2 !7 1 !2
36.
2 1 !x 3 !x
3
x 1 2 "x2 x
Simplify. Assume that all the variables are positive. 37. !28 1 4 !63 2 2 !7 12 !7
38. 6 !40 2 2 !90 2 3 !160 26 !10
39. 3 !12 1 7 !75 2 !54 41 !3 2 3 !6
3 3 40. 4 !81 1 2 !72 2 3 !24 6 !3 1 4 !9
41. 3 !225x 1 5 !144x 105 !x
42. 6"45y2 1 4"20y2 26y !5
43. A3 !y 2 !5B A2 !y 1 5 !5B 6y 1 13 !5y 2 25
44. A !x 2 !3B A !x 1 !3B
3
3
3
x23
300 ft
300 V3 ft
600 ft
sidewalk
45. A park in the shape of a triangle has a sidewalk dividing it into two parts.
300 V6 ft
300 V3 ft
a. If a man walks around the perimeter of the park, how far will he walk? (900 1 300 !3 1 300 !6) ft or about 2154 ft b. What is the area of the park? 270,000 1 90,000 !3 2
ft2 or about 212,942 ft2
46. The area of a rectangle is 10 in.2. The length is A2 1 !2B in. What is the width? 5(2 2 !2) in. 47. One solution to the equation x2 1 2x 2 2 5 0 is 21 1 !3. To show this,
let x 5 21 1 !3 and answer each of the following questions.
a. What is x2? 4 2 2 !3 b. What is 2x? 22 1 2 !3 c. Using your answers to parts (a) and (b), what is the sum x2 1 2x 2 2? 0
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
24
Name
6-3
Class
Date
Practice
Form K
Binomial Radical Expressions
Simplify if possible. To start, determine if the expressions contain like radicals. 3
1. 3 !5 1 4 !5
both radicals 7 !5
3
2. 8 !4 2 6 !4 3 2 !4
3. 2 !xy 1 2 !y no; cannot simplify
4. A floor tile is made up of smaller squares. Each square measures 3 in. on each side. Find the perimeter of the floor tile. 24 !2 in.
Simplify. To start, factor each radicand. 4
5. !18 1 !32
4
6. !324 2 !2500 4
22 !4 or 22 !2
5 !9 ? 2 1 !16 ? 2 7 !2
3
3
7. !192 1 !24 3
6 !3
Multiply. 8. A3 2 !6B A2 2 !6B 12 2 5 !6
9. A5 1 !5B A1 2 !5B 24 !5
10. A4 1 !7B 2 23 1 8"7
Multiply each pair of conjugates. 11. A7 2 !2B A7 1 !2B 47
12. A1 1 3 !3B A1 2 3 !3B 226
13. A6 1 4 !7B A6 2 4 !7B 276
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
25
Name
Class
6-3
Date
Practice (continued)
Form K
Binomial Radical Expressions
Rationalize each denominator. Simplify the answer. 14.
3 2 1 !6
5
15.
2 2 !6 3 ? 2 1 !6 2 2 !6
7 1 !5 6 2 !5
16.
47 1 13 !5 31
1 2 2 !10 4 1 !10 4 2 32 !10
23 1 32 !6
17. A section of mosaic tile wall has the design shown at the
right. The design is made up of equilateral triangles. Each side of the large triangle is 4 in. and each side of a small triangle is 2 in. Find the total area of the design to the nearest tenth of an inch. A N 17.3 in.2
Simplify. Assume that all variables are positive. 18. !45 2 !80 1 !245 6 !5
19. A2 2 !98B A3 1 !18B 236 2 15 !2
21. Error Analysis A classmate simplified the 1 using the steps shown. expression 1 2 !2
What mistake did your classmate make?
20. 6"192xy2 1 4"3xy2 52y !3x
1 2 !2 1 ? 1 2 !2 1 2 !2 1 2 !2
5 122 5
1 2 !2 5 21 1 !2 21
What is the correct answer? The student multiplied the denominator by itself instead of by its conjugate; 21 2 !2
22. Writing Explain the first step in simplifying !405 1 !80 2 !5. First, factor each radicand so you can combine like radicals.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
26
Name
Class
6-3
Date
Standardized Test Prep Binomial Radical Expressions
Multiple Choice For Exercises 1−5, choose the correct letter. 1. What is the simplest form of 2!72 2 3 !32? D
2 !72 2 3 !32
24 !2
22 !2
0
2. What is the simplest form of A2 2 !7B A1 1 2 !7B? F
212 1 3 !7
16 1 5 !7
212 2 3 !7
3 1 !7
3. What is the simplest form of A !2 1 !7B A !2 2 !7B? C
9 1 2 !14
9 2 2 !14
4. What is the simplest form of
214 1 7 !5
25
7 ? F 2 1 !5
9
214 2 7 !5
14 1 7 !5
14 2 7 !5 3
3
3
5. What is the simplest form of 8!5 2 !40 2 2 !135? D 3 16 ! 5
3 12 ! 5
3 4! 5
0
Short Response 6. A hiker drops a rock from the rim of the Grand Canyon. The distance it falls d
in feet after t seconds is given by the function d 5 16t2 . How far has the rock fallen after (3 1 !2) seconds? Show your work. [2] d 5 16t2 5 16(3 1 !2)2 5 16(11 1 6 !2) 5 176 1 96 !2 ft [1] appropriate method but with computational errors [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
27
Name
Class
6-3
Date
Enrichment Binomial Radical Expressions
Consider how you might use a calculator to find the square of negative three. If you enter the expression 232, your calculator produces an answer of 29. However, the square of negative three is (23)2 5 (23)(23) 5 9. Calculators follow the order of operations. Therefore, a calculator will compute 232 as the opposite of 32. The correct input is (23)2 , which is correctly evaluated as 9. Be sure to follow the order of operations when expanding binomial radical expressions. 1. Consider the algebraic expression (a 1 b)2 . Is (a 1 b)2 equivalent to a2 1 b2 ?
If yes, explain. If not, explain why it is not mathematically logical and give a counterexample. Answer may vary. Sample: (a 1 b)2 means (a 1 b)(a 1 b) which, when expanded, is a2 1 2ab 1 b2 , which is not equivalent to a2 1 b2 .
2. Are there values of a and b for which (a 1 b)2 5 a2 1 b2 ? Answers may vary. Sample: a 5 1, b 5 0
Consider each pair of expressions below for nonnegative values of the variables. State whether they are equivalent expressions. If yes, explain. If not, give a counterexample. 3. "x2 1 y2, "x2 1 "y2 Answers may vary. Sample: These expressions are not equivalent. Let x 5 2 and y 5 3 then "22 1 32 5 "13 u "4 1 "9 "a
a
4. b , Åb Answers may vary. Sample: These expressions are not equivalent. Let a = 6 and !6
b 5 2 then 2 N 1.22 and Å62 5 !3 N 1.73 5. Q !a R 2, a Answers may vary. Sample: These expressions are equivalent. A !aB 2 5 A !aB A !aB 5 "a2 5 a for all a L 0. 2
6. Q "x2 1 y2 R , x 1 y Answers may vary. Sample: These expressions are not equivalent. Q "x2 1 y2 R Q "x2 1 y2 R 5 "(x2 1 y2)2 5 x2 1 y2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
28
Name
Class
Date
Reteaching
6-3
Binomial Radical Expressions
Two radical expressions are like radicals if they have the same index and the same radicand. Compare radical expressions to the in a polynomial expression. Like :
4x3
11x3
Unlike :
4y3
11x3
Like radicals:
4!6
3
3 11 ! 6
Unlike radicals:
4!5
3
3 11 ! 6
The power and the variable are the same 4y2
Either the power or the variable are not the same. The index and the radicand are the same
2
4 "6
Either the index or the radicand are not the same.
When adding or subtracting radical expressions, simplify each radical so that you can find like radicals. Problem
What is the sum? !63 1 !28 !63 1 !28 5 !9 ? 7 1 !4 ? 7
Factor each radicand.
5 "3 2 ? 7 1 "2 2 ? 7
Find perfect squares.
5 "3 2 "7 1 "2 2 "7
n n n Use !ab 5 !a ? !b.
5 3 !7 1 2 !7
Use "an 5 a to simplify.
5 5 !7
Add like radicals.
n
The sum is 5!7.
Exercises Simplify. 1. !150 2 !24 3 !6 3
3
3
4. 5 !2 2 !54 2 !2
3
3
3
2. !135 1 !40 5 !5
3. 6 !3 2 !75 !3 3
3
3
5. 2!48 1 !147 2 !27 0 6. 8 !3x 2 !24x 1 !192x 3
10 !3x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
29
Name
Class
Date
Reteaching (continued)
6-3
Binomial Radical Expressions
• Conjugates, such as !a 1 !b and !a 2 !b, differ only in the sign of the second term. If a and b are rational numbers, then the product of conjugates produce a rational number: 2
2
Q !a 1 !b R Q !a 2 !b R 5 Q !a R 2 Q !b R 5 a 2 b.
• You can use the conjugate of a radical denominator to rationalize the denominator. Problem
What is the product? Q 2 !7 2 !5 R Q 2 !7 1 !5 R Q 2 !7 2 !5 R Q 2 !7 1 !5 R These are conjugates. 2
5 Q 2 !7 R 2 Q !5 R
2
Use the difference of squares formula.
5 28 2 5 5 23
Simplify.
Problem
How can you write the expression with a rationalized denominator?
4 !2 1 1 !3
4 !2 1 1 !3
5
4 !2 1 2 !3 ? 1 1 !3 1 2 !3
Use the conjugate of 1 1 !3 to rationalize the denominator.
5
4 !2 2 4 !6 123
Multiply.
5
A4 !2 2 4 !6B 4 !2 2 4 !6 5 2 22 2
Simplify.
5
24 !2 1 4 !6 5 22 !2 1 2 !6 2
Exercises Simplify. Rationalize all denominators. 7. A3 1 !6B A3 2 !6B 3 10.
2 2 !7 2 1 !7 211 1 4"7 3
8.
2 !3 1 1 "3 1 1 2 5 2 !3
11. A2 !8 2 6B A !8 2 4B 40 2 28 !2
9. Q 4 !6 2 1 R Q !6 1 4 R 12.
!5 2 1 !3 2 !5 2 !15
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
30
20 1 15 !6
Name
Class
Date
Additional Vocabulary
6-4
Rational Exponents
Choose the word or phrase from the list that best matches each sentence. rational exponent
radical form
4
1. The expression " y3 is written in rational exponent
2. A
exponential form
radical form
.
is an exponent written in fractional form.
3
3. The expression x 5 is written in
exponential form
.
Write each expression in exponential form. 7
4
4. " y7 5
y4 4
3
x3
5
a5
5. (!x)4 5
3
6. (!a)3 5 8
7. !r 5
1
r8
Write each expression in radical form. 3
4 " w3
8. w4 5 5
"b5
1
"h
9. b2 5 10. h2 5 3
7 3 11. g 7 5 "g
Multiple Choice 6 4 " y
12. What is 3 1
y2
!y
in simplest ? B 3 ! y
3 4 " y
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
31
2
y3
Name
Class
Date
Think About a Plan
6-4
Rational Exponents
Science A desktop world globe has a volume of about 1386 cubic inches. The radius of the Earth is approximately equal to the radius of the globe raised to the 10th power. Find the radius of the Earth. (Hint: Use the formula V 5 43pr3 for the volume of a sphere.) Know
z
z
1386 in.3 . 1. The volume of the globe is
2. The radius of the Earth is equal to the radius of the globe raised to the 10th power
.
Need 3. To solve the problem I need to find the radius of the Earth
Plan 4. Write an equation relating the radius of the globe rG to the radius of the
Earth rE. rE 5 rG 10
5. How can you represent the radius of the globe in of the radius of the
Earth? 1
rG 5 rE 10 6. Write an equation to represent the volume of the globe. 1386 5 43πrG3
7. Use your previous equation and your equation from Exercise 5 to write an
equation to find the radius of the Earth. 1
1386 5 43 π ¢ rE10 ≤
3
8. Solve your equation to find the radius of the Earth. about 251,000,000 in. or 3961 mi
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
32
.
Name
Class
Date
Practice
6-4
Form G
Rational Exponents
Simplify each expression. 1
1
1. 1253 5 1
1
2. 642 8
1
1
4. 72 ? 72 7 1
1
1
1
3. 325 2 1
1
5. (25)3 ? (25)3 ? (25)3 25 1
7. 113 ? 113 ? 113 11 10. 122 ? 272 18
1
1
8. 72 ? 282 14 1
1
1
1
1
1
6. 32 ? 752 15 9. 84 ? 324 4
1
11. 123 ? 453 ? 503 30
1
1
12. 182 ? 982 42
Write each expression in radical form. 4 3 13. x3 " x4
1 3 14. (2y)3 " 2y
15. a1.5 "a3
1 5 16. b5 !b
2 3 2 17. z3 " z
1 4 18. (ab)4 !ab
5 12 19. m2.4 " m
2 20. t27
21. a21.6
1 7 "t2
1 5 "a8
Write each expression in exponential form. 3
3
1
3
22. "x3 x 2
1
23. !m m3 1 2
24. !5y (5y)2 3
4
25. " 2y2 23y 3
26. Q !b R 3 b4
28. "(6a)4 36a2
29. " n4 n5
5
4
1
27. !26 (26)2 4
3
30. " (5ab)3 (5ab)4
31. The rate of inflation i that raises the cost of an item from the present value P to F 1t the future value F over t years is found using the formula i 5 Q P R 2 1. Round
your answers to the nearest tenth of a percent.
a. What is the rate of inflation for which a television set costing $1000 today will become one costing $1500 in 3 years? 14.5% b. What is the rate of inflation that will result in the price P doubling (that is, F 5 2P) in 10 years? 7.2%
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
33
Name
Class
Date
Practice (continued)
6-4
Form G
Rational Exponents
Write each expression in simplest form. Assume that all variables are positive. 1
1
32. Q 814 R 4 81
33. Q 325 R 5 32
35. 70 1
36. 83 4
1
1
34. A2564 B 4 256
2
5
1
2
37. (227)3 9 3
1
1
38. x2 ? x3 x 6
39. 2y2 ? y 2 y 2
40. A82 B 3 4
41. 3.60 1
1 1 42. Q 16 R 4 1 2
27 2 43. Q 8 R 3 9 4 1
8
44. " 0 0 1
45. 2
1
47. Q 3a2 b3 R 2 9ab3
50.
2 y5
?
1 1
59.
?
?
1 x3
3 x4
y6
1
b3
1
3
1
52. Q 2a4 R 3 8a4
2 x 21 13
1
1 2 55. Q 9x4y22 R 2 3x y
1 2
1
1 x6
3
1 4y2 2
1
2b x3
12y3
49. Q a3b22 R 26 a4
54. Q 2x5 R Q 6x4 R 12x 20
2 27x6 3 3x 56. a b 4 4 64y 4y 3 1 x4
x7
2
53. 8122 9
46.
1
2
51. a
y 40
7 12x 6
48. Q y3 R 29 y6 4
31
3 y8
1 2 Q 3x2 R Q 4x3 R
57.
x 2 y3 1 1 x 3 y2
1
5
1
1 x23 y 2 60. a 2 1 b x3 y22
1
1
58. y8 4 y2 y8
x6 y6 y3 x2
1
12x8 2 2x4 61. a b 5y5 75y10
62. In a test kitchen, researchers have measured the radius of a ball of dough
made with a new quick-acting yeast. Based on their data, the radius r of the t dough ball, in centimeters, is given by r 5 5(1.05)3 after t minutes. Round the answers to the following questions to the nearest tenth of a cm. a. What is the radius after 5 minutes? 5.4 cm b. What is the radius after 20 minutes? 6.9 cm c. What is the radius after 43 minutes? 10.1 cm
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
34
Name
Class
6-4
Date
Practice
Form K
Rational Exponents
Simplify each expression. 1
1. 16 4 4 ! 16 2
1
1
1
2. (23) 3 ? (23) 3 ? (23) 3 23
1
1
3. 5 2 ? 45 2 15
Write each expression in radical form. 1
4. x 4 4
!x
4
2
5. x 5
6. x 9
5
9
"x 4
"x 2
Write each expression in exponential form. 3
7. !2 1
23
3
3
8. " 2x2
9. " (2x)2
1
2
A2x 2 B 3
(2x) 3
10. Bone loss for astronauts may be prevented with an apparatus that rotates a0.5 , N is the rate of rotation in to simulate gravity. In the formula N 5 2pr 0.5
revolutions per second, a is the simulated acceleration in m/s2, and r is the radius of the apparatus in meters. How fast would an apparatus with the following radii have to rotate to simulate the acceleration of 9.8 m/s2 that is due to Earth’s gravity? a. r 5 1.7 m 0.382 rev/s b. r 5 3.6 m 0.263 rev/s c. r 5 5.2 m 0.218 rev/s d. Reasoning Would an apparatus with radius 0.8 m need to spin faster or slower than the one in part (a)? faster
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
35
Name
Class
Date
Practice (continued)
6-4
Form K
Rational Exponents
Simplify each number. 1
12. 2431.2 729
11. (2216) 3 3 ! 2216 26
13. 32 20.4 1 4
Find each product or quotient. To start, rewrite the expression using exponents. 4
5
3
14. A !6B A !6B 1
1
15. 12
7 5 Q 6 4 R Q 6 3 R "6
"x2 10
3
16. !20 ? !135
x2
%
6
6 "5 5
5
!x
Simplify each number. 2
2
17. (125) 3
2
18. (216) 3(216) 3
25
2
19. (2243) 5
1296
9
Write each expression in simplest form. Assume that all variables are positive. 3
20. Q 16x28 R 24 x6 8
1
x2 3 22. a 210 b x x4
1
21. Q 8x15 R 2 3 1 2x 5
23. Error Analysis Explain why the following
simplification is incorrect. What is the correct simplification? You cannot multiply 5 and 1
5 2 together by multiplying bases. You have to rewrite 5 as 51 and combine the exponents; 20 2 5 !5.
1
5Q4 2 5 2 R 1
1
5 5(4) 2 5 Q 5 2 R 5 20 2 25 2 5 15
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
36
Name
Class
Date
Standardized Test Prep
6-4
Rational Exponents
Multiple Choice For Exercises 1−5, choose the correct letter. 1
1
1
1. What is 123 ? 453 ? 503 in simplest form? B
!27,000 1
1
30
1073
27,000
3 " (xy)2
3 2 " xy
2
2. What is x3 ? y3 in simplest form? I
x3"y3 1
"xy3 1
1
3. What is x3 ? x2 ? x4 in simplest form? A 13
1
x 12
1
x 24
x 24
1
x
5 xy 2
y2
6
2 1
4. What is £
5
x9
x3y3
1 3≥
in simplest form? I
x2y4 5
5
x 7y 2
xy 2
5
1
5. What is (232x10 y35)25 in simplest form? C 2 2 2 7 x y
2x2y7
2
1 2x2 y7
2 x2 y7
Short Response 6. The surface area S, in square units, of a sphere with volume V, in cubic units, 1
2
is given by the formula S 5 p 3(6V )3 . What is the surface area of a sphere with volume 43 mi3? Show your work. 1
2
1
2 3
1
2
1
2
[2] S 5 π 3 (6V) 3 5 π 3 c 6 Q 43 R d 5 π 3 (8) 3 5 4π 3 mi
[1] appropriate method but some computational errors [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
37
Name
6-4
Class
Date
Enrichment Rational Exponents
Power Games Each problem below involves rational exponents. Some of the problems are tricky. Good luck! 1. Begin with any positive number. Call it x. Divide x by 2. Call the result r. Now
follow these directions carefully. You may use a calculator. final r 5 !x Divide x by r. Call the result q. Add q and r. Call the result s. Divide s by 2. Call the result r. Go back to step a. Repeat steps a–d until r no longer changes. What is the relationship between the original x and the final result?
a. b. c. d.
2. If we take the square root of a number 6 times, it would look like this:
'& $#" !x Rewrite the expression above using rational exponents.
1 1 1 1 1 1 2 2 2 2 2 a a a a ax2 b b b b b
Simplify the expression above. Express the denominator of the exponent as a 1 power of 2. x64 ; 26 If you were to take the square root of a number 10 times, what would the 10 12 denominator of the exponent be equal to if you use rational exponents? 12 times? 2 ; 2 Choose any number and repeatedly take the square root. What number is the answer approaching? 1 Does the answer appear to approach the same number if you change the number you choose? yes In Exercises 3–6, assume that the square roots and the operations inside them repeat forever. 3. How much is $2 3 #2 3 "2 3 !2 3 c? (Hint: Let
y 5 $2 3 #2 3 "2 3 !2 3 c. Then use substitution and solve the equation y 5 "2 3 y.) 2 4. How much is $2 1 #2 1 "2 1 !2 1 c? 2 5. How much is $2 2 #2 2 "2 2 !2 2 c? 1 3 6. How much is $2 4 #2 4 "2 4 !2 4 c? " 2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
38
Name
Class
Date
Reteaching
6-4
Rational Exponents
You can simplify a number with a rational exponent by converting the expression to a radical expression: 1
1 2 92 5 !9 53
n
xn 5 !x, for n . 0
1 3 83 5 ! 852
You can simplify the product of numbers with rational exponents m and n by raising the number to the sum of the exponents using the rule am ? an 5 am1n Problem
What is the simplified form of each expression? 1
1
1
1
a. 364 ? 364 1
1
364 ? 364 5 364 1 4
Use am ? an 5 am1n .
1
5 362
Add.
2 5 !36
Use xn 5 !x.
56
Simplify.
1
n
3
2
b. Write Q 6x3 R Q 2x4 R in simplified form. 3
2
Q 6x3 R Q 2x4 R
3
2
5 6 ? 2 ? x3 ? x4 2
Commutative and Associative Properties of Multiplication
3
5 6 ? 2 ? x3 1 4
Use xm ? xn 5 xm1n.
17
5 12x12
Simplify.
Exercises Simplify each expression. Assume that all variables are positive. 1
2
1
2 1
1
7
2. Q 2y4 R Q 3y3 R 6y 12
1. 53 ? 53 5 13
4. 2y3 y5 2y 15
1
1
1
1
5. 54 ? 54 !5
1
2
6. Q 23x 6 R Q 7x 6 R 221 !x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
39
1
3. (211)3 ? (211)3 ? (211)3 211
Name
Class
Date
Reteaching (continued)
6-4
Rational Exponents
To write an expression with rational exponents in simplest form, simplify all exponents and write every exponent as a positive number using the following rules for a 2 0 and rational numbers m and n: 1 a2n 5 n a
1 a2m
5 am
(am)n 5 amn
(ab)m 5 ambm
Problem 2
What is A8x9y23 B 23 in simplest form? 2
(8x9y23)23
2
5 A23 x9 y23 B 23 2
2
Factor any numerical coefficients. 2
5 A23 B 23 Ax9 B 23 Ay23 B 23
Use the property (ab)m 5 ambm.
5 222x26y2
Multiply exponents, using the property (am)n 5 amn.
y2 5 2 6 2 x y2 5 6 4x
Write every exponent as a positive number. Simplify.
Exercises Write each expression in simplest form. Assume that all variables are positive. 1
1
7. A16x2 y8 B 22 4xy4 1
10. A25x26 y2 B 2 5y x3
1
8. Az23 B 9
1
1 4
9. Q 2x4 R
1 z3
16z4 12. a b 25x8
2
11. A8a23 b9 B 3 4b6 a2
1
x2 5 2 1 13. a 21 b x 5y 5 y 3
16. A9z10 B 2 27z15
16x 1
22
1
2
14. A27m9 n23 B 23
1
17. (2243)25 21 3
n2 9m6
1
32r2 4 15. a 4 b 2r 2 2s s 2 x5 10 18. a 1 b y2
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
40
5x4 4z2
x4 y5
Name
Class
6-5
Date
Additional Vocabulary Solving Square Root and Other Radical Equations
Problem 3 Solve the equation 4" (y 1 2)2 1 3 5 19. Justify your steps. Then check your solution. 2
4(y 1 2)3 1 3 5 19 2
4(y 1 2)3 5 16 2
(y 1 2)3 5 4 2 3
3 2
Subtract 3 from each side. Divide each side by 4.
3
c(y 1 2) d 5 42 (y 1 2) 5 8 y56 3 4" (6 1 2)2 1 3 0 19
Check
Rewrite the radical using a rational exponent.
3 2 4" 8 1 3 0 19
4 ? 4 1 3 0 19 19 5 19
3
Raise each side to the 2 power. Simplify. Solve for y. Substitute 6 for y. Add. Simplify the radical. Simplify.
Exercise Solve the equation 9"(2x 2 4)4 1 2 5 38. Justify your steps. Then check your solution. 4
9(2x 2 4)2 1 2 5 38 9(2x 2 4)2 5 36
1
c(2x 2 4)2 d 5 42 (2x 2 4) 5 2 x53 Check
Subtract 2 from each side and simplify the exponent. Divide each side by 9.
(2x 2 4)2 5 4 1 2
Rewrite the radical using a rational exponent.
9"(2 ? 3 2 4)4 1 2 0 38 9"16 1 2 0 38 38 5 38
Raise each side to the 12 power. Simplify. Solve for x. Substitute 3 for x. Simplify the expression under the radical sign. Simplify.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
41
Name
6-5
Class
Date
Think About a Plan Solving Square Root and Other Radical Equations
Traffic Signs A stop sign is a regular octagon, formed by cutting triangles off the corners of a square. If a stop sign measures 36 in. from top to bottom, what is the length of each side? Understanding the Problem x
1. How can you use the diagram at the right to find a
relationship between s and x? s
Since the triangles are right triangles, use the Pythagorean Theorem to relate s and x
.
36 in.
2. How can you use the diagram at the right to find another
x
s
x
relationship between s and x? The length of a side of the square, which is s 1 2x, is the same as the height of the stop sign from top to bottom
.
3. What is the problem asking you to determine? the length s of each side of the stop sign
Planning the Solution 4. What are two equations that relate s and x? 2x2 5 s2 ; 2x 1 s 5 36 5. How can you use your equations to find s? Solve the first equation for x and substitute the result into the second equation
.
Getting an Answer 6. Solve your equations for s. about 14.9 in. 7. Is your answer reasonable? Explain. Yes; the length of one side of the stop sign is a little more than a third of the total height of the sign
. Prentice Hall Algebra 2 • Teaching Resources
Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
42
Name
Class
Date
Practice
6-5
Form G
Solving Square Root and Other Radical Equations
Solve. 1. 5 !x 1 2 5 12 4
2. 3 !x 2 8 5 7 25
3. !4x 1 2 5 8 9
4. !2x 2 5 5 7 27
5. !3x 2 3 2 6 5 0 13
6. !5 2 2x 1 5 5 12 222
7. !3x 2 2 2 7 5 0 17
8. !4x 1 3 1 2 5 5 32
9. !33 2 3x 5 3 8
3
3
10. !2x 1 1 5 3 13
11. !13x 2 1 2 4 5 0 5
3
12. !2x 2 4 5 22 22
Solve. 1
1
13. (x 2 2) 3 5 5 127
14. (2x 1 1)3 5 23 214
1
1
16. 2x 3 2 2 5 0 1
17. x 2 2 5 5 0 25
1
1
19. (7x 2 3)2 5 5 4
20. 4x 2 2 5 5 27 64
1
2
22. (2x 1 1)3 5 1 0
3
15. 2x 4 5 16 16 3
18. 4x 2 2 5 5 103 9 1
21. x 6 2 2 5 0 64 4
23. (x 2 2)3 2 4 5 5 29, 225 24. 3x 3 1 5 5 53 8, 28
25. The formula P 5 4"A relates the perimeter P, in units, of a square to its area A, in square units. What is the area of the square window shown below? 36 ft2
Perimeter: 24 ft
2
26. The formula A 5 6V 3 relates the surface area A, in square units, of a cube to
the volume V, in cubic units. What is the volume of a cube with surface area 486 in.2? 729 in.3 27. A mound of sand at a rock-crushing plant is growing over time. The equation
3 t5 ! 5V 2 1 gives the time t, in hours, at which the mound has volume V, in cubic meters. When is the volume equal to 549 m3? 14 h
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
43
Name
Class
Date
Practice (continued)
6-5
Form G
Solving Square Root and Other Radical Equations
28. City officials conclude they should budget s million dollars for a new library
building if the population increases by p thousand people in a ten-year census. The 2 formula s 5 2 1 13(p 1 1)5 expresses the relationship between population and library budget for the city. How much can the population increase without the city going over budget if they have $5 million for a new library building? 242,000
Solve. Check for extraneous solutions. 29. !x 1 1 5 x 2 1 3
30. !2x 1 1 5 23 no solution
1
1
31. (x 1 7)2 5 x 2 5 9
32. (2x 2 4)2 5 x 2 2 2, 4
33. !x 1 2 5 x 2 18 23
34. !x 1 6 5 x 9
1
1
35. (2x 1 1)2 5 25 no solution
36. (x 1 2)2 5 10 2 x 7
37. !x 1 1 5 x 1 1 21, 0
38. !9 2 3x 5 3 2 x 0, 3
3
5
39. !2x 2 4 5 22 22
40. 2 !5x 1 2 2 1 5 3 6
41. !4x 1 2 5 !3x 1 4 2
42. !7x 2 6 2 !5x 1 2 5 0 4
1
1
1
1
43. 2(x 2 1)2 5 (26 1 x)2 10
44. (x 2 1)2 2 (2x 1 1)4 5 0 4
45. !2x 2 !x 1 1 5 1 8
46. !7x 2 1 5 !5x 1 5 3
1
1
1
1
47. (7 2 x)2 5 (2x 1 13)2 22
48. (x 2 7)2 5 (x 1 5)4 11
49. !x 1 9 2 !x 5 1 16
50. !8x 2 !6x 2 2 5 0 21
3
3
51. A clothing manufacturer uses the model a 5 !f 1 4 2 !36 2 f to estimate
the amount of fabric to order from a mill. In the formula, a is the number of apparel items (in hundreds) and f is the number of units of fabric needed. If 400 apparel items will be manufactured, how many units of fabric should be ordered? 32 52. What are the lengths of the sides of the trapezoid shown at the right if the
perimeter of the trapezoid is 17 cm?
x
x 5 4 cm, 2 !x 5 4 cm, x 1 1 5 5 cm 2 Vx
2 Vx x⫹1
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
44
Name
Class
Date
Practice
6-5
Form K
Solving Square Root and Other Radical Equations
Solve. To start, rewrite the equation to isolate the radical. 1. !x 1 2 2 2 5 0
2. !2x 1 3 2 7 5 0 23
!x 1 2 5 2 2
3. 2 1 !3x 2 2 5 6 6
Solve. 3
2
4. 2(x 2 2) 3 5 50
5. 2(x 1 3) 2 5 54 6
127 and 2123
1
6. (6x 2 5) 3 1 3 5 22 220
V
7. The formula d 5 2#ph relates the diameter d, in units, of a cylinder to its
volume V, in cubic units, and its height h, in units. A cylindrical can has a diameter of 3 in. and a height of 4 in. What is the volume of the can to the nearest cubic inch? 28 in.3
8. Writing Explain the difference between a radical equation and a polynomial equation. A radical equation has a variable in a radicand or a variable with a rational exponent, while a polynomial equation has a variable with whole number exponents.
3
9. Reasoning If you are solving 4(x 1 3) 4 5 7, do you need to use the absolute value to solve for x? Why or why not? No; the numerator of the exponent 34 is not even.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
45
Name
Class
Date
Practice (continued)
6-5
Form K
Solving Square Root and Other Radical Equations
Solve. Check for extraneous solutions. First, isolate a radical, then square each side of the equation. 10. !4x 1 5 5 x 1 2
A !4x 1 5B 2 5 (x 1 2)2
11. !23x 2 5 2 3 5 x 22
12. !x 1 7 1 5 5 x 9
1 and 21
13. !2x 2 7 5 !x 1 2
A !2x 2
7B 2
5 A !x 1
2B 2
14. !3x 1 2 2 !2x 1 7 5 0 15. !2x 1 4 2 2 5 !x 5 0 and 16
9
16. Find the solutions of !x 1 2 5 x. 2 a. Are there any extraneous solutions? 21 b. Reasoning How do you know the answer to part (a)? Substitute the solutions into the original equation. If a solution does not make the equation true, then the solution is extraneous.
17. A floor is made up of hexagon-shaped tiles. Each hexagon tile has
an area of 1497 cm2. What is the length of each side of the hexagon? (Hint: Six equilateral triangles make one hexagon.) about 24 cm s s!3 2
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
46
Name
Class
Date
Standardized Test Prep
6-5
Solving Square Root and Other Radical Equations
Gridded Response Solve each exercise and enter your answer in the grid provided. 1. What is the solution? !2x 2 4 2 3 5 1
1
2. What is the solution? 5x 2 2 8 5 7
3. What is the solution? !2x 2 6 5 3 2 x
4. What is the solution? !5x 2 3 5 !2x 1 3
5. Kepler’s Third Law of Orbital Motion states that the period P (in Earth years)
it takes a planet to complete one orbit of the sun is a function of the distance d (in astronomical units, AU) from the planet to the sun. This relationship is 3 P 5 d 2 . If it takes Neptune 165 years to orbit the sun, what is the distance (in AU) of Neptune from the sun? Round your answer to two decimal places.
Answers 1.
–
10 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
2. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
9 0 1 2 3 4 5 6 7 8 9
3. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
3 0 1 2 3 4 5 6 7 8 9
4. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
–
2 0 1 2 3 4 5 6 7 8 9
5. 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
47
–
30 . 08 0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9
0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9
Name
Class
Date
Enrichment
6-5
Solving Square Root and Other Radical Equations
When solving radical equations you will often get an extraneous solution. You can use a graph to explain why an algebraic answer is not a solution. 1. Solve the equation !x 1 2 5 x 2 4. Is there an extraneous solution? 7; 2 is an extraneous solution.
2. To analyze this equation with a graph, rewrite the equation as a system of two
equations. What two equations can you write? y 5 !x 1 2 and y 5 x 2 4
8 y 4 ᎐8 ᎐4 O ᎐4
3. Graph the two equations.
x 4
8
᎐8
4. Explain how you find the solution to this system of equations on your graph.
What is the solution?
Answers may vary. Sample: On a graph the solution to a system of equations is the point of intersection; the solution for this system is (7, 3).
5. How can you use the solution from the graph of the system of equations to
help you solve the original equation !x 1 2 5 x 2 4? Answers may vary. Sample: The x-coordinate of the solution to the system is the solution to the original equation. 6. How can you tell from your graph that one of your algebraic answers is an
extraneous solution? Answers may vary. Sample: Because there is only one point of intersection, there can only be one solution to the equation.
Solve each equation. Graph each equation as a system to determine if there are any extraneous solutions. 7. !4x 1 1 5 3
8. x 5 !6 2 x
8 y
8 y
4 ᎐8 ᎐4 O ᎐4
9. !x 1 1 5 x 2 1
4
8 y
4
x 8
⫺4 ⫺4
᎐8
4
8
⫺8
2; no extraneous solutions
4
x
⫺4 ⫺4
x 4
8
⫺8
2; 23 is an extraneous solution.
3; 0 is an extraneous solution.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
48
Name
Class
Date
Reteaching
6-5
Solving Square Root and Other Radical Equations
Equations containing radicals can be solved by isolating the radical on one side of the equation, and then raising both sides to the same power that would undo the radical. Problem
What is the solution of the radical equation? 2!2x 1 2 2 2 5 10 2 !2x 1 2 2 2 5 10 2 !2x 1 2 5 12
Add 2 to each side.
!2x 1 2 5 6
Divide each side by 2.
(!2x 1 2)2 5 62
Square each side to undo the radical.
2x 1 2 5 36
Simplify.
2x 5 34
Subtract 2 from each side.
x 5 17
Divide each side by 2.
Check the solution in the original equation. Check 2 !2x 1 2 2 2 5 10 2 !2(17) 1 2 2 2 0 10 2 !36 2 2 0 10
Write the original equation. Replace x by 17. Simplify.
12 2 2 0 10 10 5 10 The solution is 17.
Exercises Solve. Check your solutions. 1
2. 3 !2x 5 12 8
1. x 2 5 13 169 1
4. (3x 1 4)2 2 1 5 4 7 1
7. (x 1 2) 2 2 5 5 0 23
1
3. !3x 1 5 5 11 12
5. (6 2 x) 2 1 2 5 5 23
6. !3x 1 13 5 4 1
8. !3 2 2x 2 2 5 3 211
3 9. !5x 1 2 2 3 5 0 5
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
49
Name
Class
6-5
Date
Reteaching (continued) Solving Square Root and Other Radical Equations
An extraneous solution may satisfy equations in your work, but it does not make the original equation true. Always check possible solutions in the original equation. Problem
What is the solution? Check your results. !17 2 x 2 3 5 x !17 2 x 2 3 5 x !17 2 x 5 x 1 3
Add 3 to each side to get the radical alone on one side of the equal sign.
A !17 2 xB 2 5 (x 1 3)2
Square each side.
17 2 x 5 x2 1 6x 1 9 0 5 x2 1 7x 2 8
Rewrite in standard form.
0 5 (x 2 1)(x 1 8)
Factor.
x 2 1 5 0 or x 1 8 5 0 x 5 1 or
Set each factor equal to 0 using the Zero Product Property.
x 5 28
Check !17 2 x 2 3 5 x !17 2 1 2 3 0 1 !16 2 3 0 1 151
!17 2 x 2 3 5 x !17 2 (28) 2 3 0 28 !25 2 3 0 28 2 2 28
The only solution is 1.
Exercises Solve. Check for extraneous solutions. 10. !5x 1 1 5 !4x 1 3 2
11. !x2 1 3 5 x 1 1 no 12. !3x 5 !x 1 6 3 solution
13. x 5 !x 1 7 1 5 9
14. x 2 3 !x 2 4 5 0 16
15. !x 1 2 5 x 2 4 7
16. !2x 2 10 5 x 2 5 5, 7
17. !3x 2 6 5 2 2 x 2
18. !x 2 1 1 7 5 x 10
19. !5x 1 1 5 !3x 1 15 7 20. !x 1 9 5 x 1 7 25
21. x 2 !x 1 2 5 40 47
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
50
Name
Class
6-6
Date
Additional Vocabulary Function Operations
Darnell wrote the steps to compose the following functions on index cards, but the cards got mixed up. Let f (x) 5 x 1 7 and g(x) 5 x3. What is (g + f )(24)?
Subtract 4 from 7.
Substitute 24 for x in f(x).
Raise 3 to the 3rd power.
Substitute 3 into g(x).
Use the note cards to write the steps in order. 1. First, substitute 24 for x in f(x) . 2. Second, subtract 4 from 7 . 3. Then, substitute 3 into g(x) . 4. Finally, raise 3 to the 3rd power .
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
51
Name
6-6
Class
Date
Think About a Plan Function Operations
Sales A salesperson earns a 3% bonus on weekly sales over $5000. Consider the following functions. g(x) 5 0.03x
h(x) 5 x 2 5000
a. Explain what each function above represents. b. Which composition, (h + g)(x) or (g + h)(x), represents the weekly bonus?
Explain. 1. What does x represent in the function g(x)? the sales amount used to calculate a 3% bonus 2. What does the function g(x) represent? the bonus earned by the salesperson on sales 3. What does x represent in the function h(x)? the total weekly sales made by the salesperson 4. What does the function h(x) represent? the weekly sales over $5000 made by the salesperson 5. What is the meaning of (h + g)(x)? First multiply the value of x by 0.03, then subtract 5000 from the result
.
6. Assume that x is $7000. What is (h + g)(x)? −4790 7. What is the meaning of (g + h)(x)? First subtract 5000 from the value of x, then multiply the result by 0.03
.
8. Assume that x is $7000. What is (g + h)(x)? 60 9. Which composition represents the weekly bonus? Explain (g + h)(x) represents the weekly bonus because you must first find the sales amount over 5000 by subtracting 5000 from the weekly sales, and then you multiply the result by the bonus percent as a decimal, or 0.03
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
52
.
Name
6-6
Class
Date
Practice
Form G
Function Operations
Let f (x) 5 4x 21 and g(x) 5 2x2 1 3. Perform each function operation and then find the domain. 1. ( f 1 g)(x) 2x2 1 4x 1 2; all real numbers 4. ( f ? g) (x) 8x3 2 2x2 1 12x 23; all real numbers
2. ( f 2 g)(x) 22x2 + 4x 24; all real numbers f 5. g (x) 4x 2 1 ; 2x2 1 3
3. (g 2 f )(x) 2x2 2 4x 1 4; all real numbers g 6. (x) f
all real numbers
2x2 1 3 4x 2 1 ;
all real numbers except 14
Let f (x) 5 2x and g(x) 5 !x 21. Perform each function operation and then find the domain of the result. 7. ( f 1 g)(x)
8. ( f 2 g)(x)
9. (g 2 f )(x)
2x 2 "x 1 1; x L 0
2x 1 "x 2 1; x L 0
f 11. g (x)
10. ( f ? g)(x)
2x ; !x 2 1
2x"x 2 2x; x L 0
22x 1 "x 2 1; x L 0
g 12. (x) f x L 0 and x u 1
"x 2 1 2x ; x S 0
x
Let ƒ(x) 5 23x 1 2, g(x) 5 5 , h(x) 5 22x2 1 9, and j(x) 5 5 2 x. Find each value or expression. 13. ( f + j)(3) 24
14. ( j + h)(21) 22
15. (h + g)(25) 7
17. ƒ(x) 1 j(x) 24x 1 7
18. ƒ(x) 2 h(x) 2x2 2 3x 2 7
19. (g + f )(25) 5
20. ( f + g)(22) 16 5
21. 3ƒ(x) 1 5g(x) 28x 1 6
22. g( f (2)) 2 4 5
23. g( f (x)) 23x 1 2
24. f (g(1)) 7
16. (g + f )(a) 23a 1 2 5
17
5
5
25. A video game store adds a 25% markup on each of the games that it sells.
In addition to the manufacturer’s cost, the store also pays a $1.50 shipping charge on each game. a. Write a function to represent the price f (x) per video game after the store’s markup. f(x) 5 1.25x b. Write a function g(x) to represent the manufacturer’s cost plus the shipping charge. g(x) 5 x 1 1.5 c. Suppose the manufacturer’s cost for a video game is $13. Use a composite function to find the cost at the store if the markup is applied after the shipping charge is added. f(g(13)) N $18.13 d. Suppose the manufacturer’s cost for a video game is $13. Use a composite function to find the cost at the store if the markup is applied before the shipping charge is added. g(f(13)) 5 $17.75 Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
53
Name
Class
6-6
Date
Practice (continued)
Form G
Function Operations
4 26. The formula V 5 3 π r 3 expresses the relationship between the volume V and
radius r of a sphere. A weather balloon is being inflated so that the radius is changing with respect to time according to the equation r 5 t 1 1, where t is the time, in minutes, and r is the radius, in feet. a. Write a composite function f (t) to represent the volume of the weather balloon after t minutes. Do not expand the expression. f(t) 5 43 π(t 1 1)3 b. Find the volume of the balloon after 5 minutes. Round the answer to two decimal places. Use 3.14 for π. 904.32 ft3
27. A boutique prices merchandise by adding 80% to its cost. It later decreases by
25% the price of items that do not sell quickly. a. Write a function f (x) to represent the price after the 80% markup. f(x) 5 1.8x b. Write a function g(x) to represent the price after the 25% markdown. g(x) 5 0.75x c. Use a composition function to find the price of an item, after both price adjustments, that originally costs the boutique $150. g(f (150)) 5 $202.50 d. Does the order in which the adjustments are applied make a difference? Explain. No; it doesn’t matter whether you first multiply by 0.75 or by 1.8. 28. A department store has marked down its merchandise by 25%. It later
decreases by $5 the price of items that have not sold. a. Write a function f (x) to represent the price after the 25% markdown. f(x) 5 0.75x b. Write a function g(x) to represent the price after the $5 markdown. g(x) 5 x 2 5 c. Use a composition function to find the price of a $50 item after both price adjustments. g(f (50)) 5 $32.50 d. Does the order in which the adjustments are applied make a difference? Explain. Yes; multiplying by 0.75 and then subtracting by 5 is different than subtracting by 5 and then multiplying by 0.75.
Let g(x) 5 x2 2 5 and h(x) 5 3x 1 2. Perform each function operation. 29. (h + g)(x) 3x2 2 13
30. g(x) ? h(x) 3x3 1 2x2 2 15x 2 10
31. 22g(x) 1 h(x) 22x2 1 3x 1 12
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
54
Name
Class
6-6
Date
Practice
Form K
Function Operations
Let f (x) 5 4x 1 8 and g(x) 5 2x 2 12. Perform each function operation and then find the domain of the result. 1. ( f 1 g)(x)
(f ? g) (x)
(f 2 g) (x)
f (x) 1 g(x) (f 1 g) (x) 5 6x 2 4; all real numbers
f 4. a g b(x)
3. ( f ? g)(x)
2. ( f 2 g)(x)
f
5 2 32x 2 96; all real numbers
5 2x 1 20; all real numbers
2x 1 4
Q g R (x) 5 x 2 6 ;
8x2
all real numbers, xu6
Let f (x) 5 x 1 2 and g(x) 5 !x 2 1. Perform each function operation and then find the domain of the result. f 7. a g b(x)
6. ( f ? g)(x)
5. ( f 1 g)(x) (f 1 g)(x) 5 x 1 !x 1 1; all x L 0
g 8. a b(x) f
(f ? g)(x) f x 1 2 Q R (x) 5 ; !x 2 1 5 x !x 2 x 1 2 !x 2 2; g all x L 0, x u 1 all x L 0
g
all x L 0
Let f (x) 5 x 2 2 and g(x) 5 x2 . Find each value. To start, use the definition of composing functions to find a function rule. 9. (g f )(4)
°
10. ( f g)(21) 21
°
f (4) 5 4 2 2 5 2 4
11. (g f )(23)
°
25
Let f (x) 5 !x and g(x) 5 (x 1 2)2 . Find each value. 12. ( f g)(25)
°
3
13. ( f g)(0)
°
2
14. (g f )(4)
°
16
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
55
!x 2 1
Q f R (x) 5 x 1 2 ;
Name
Class
Date
Practice (continued)
6-6
Form K
Function Operations
15. A car dealer offers a 15% discount off the list price x of any car on the lot. At the same
time, the manufacturer offers a $1000 rebate for each purchase of a car. a. Write a function f (x) to represent the price after discount. f(x) 5 0.85x b. Write a function g (x) to represent the price after the $1000 rebate. g(x) 5 x 2 1000 c. Suppose the list price of a car is $18,000. Use a composite function to find the price of the car if the discount is applied before the rebate. $14,300 d. Suppose the list price of a car is $18,000. Use a composite function to find the price of the car if the discount is applied after the rebate. $14,450 e. Reasoning Between parts (c) and (d), will the dealer want to apply the discount before or after the rebate? Why? After; they will make more money selling the car for a higher price.
16. Error Analysis f (x) 5 2 !x and g(x) 5 3x 2 6. Your friend gives a domain f for a g b(x) as x $ 0. Is this correct? If not, what is the correct domain? No; the correct domain is x L 0, x u 2.
Let f (x) 5 2x2 2 3 and g(x) 5
x11 2 . Find each value.
17. f (g(2)) 3
18. g( f (23)) 8
2
19. ( f f )(21) 21
°
20. Reasoning A local bookstore has a sale on all their paperbacks giving a 10% discount.
You also received a coupon in the mail for $4 off your purchase. If you buy 2 paperbacks at $8 each, is it less expensive for you to apply the discount before the coupon or after the coupon? How much will you save? before the coupon; $.40
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
56
Name
Class
6-6
Date
Standardized Test Prep Function Operations
Multiple Choice For Exercises 125, choose the correct letter. 1. Let f (x) 5 22x 1 5 and g(x) 5 x3. What is (g 2 f )(x)? B
x3 2 2x 1 5
2x3 2 2x 1 5
x3 1 2x 2 5
2x3 1 2x 2 5
2. Let f (x) 5 3x and g(x) 5 x2 1 1. What is ( f · g)(x)? H
9x2 1 3x
9x2 1 1
3x3 1 3x
3x3 1 1 f
3. Let f (x) 5 x2 2 2x 2 15 and g(x) 5 x 1 3. What is the domain of g (x)? C
all real numbers
x 2 23
x 2 5, 23
x.0
4. Let f (x) 5 !x 1 1 and g(x) 5 2x 1 1. What is (g + f )(x)? F
2 !x 1 3
!2x 1 1 1 1
2x !x 1 2x 1 !x 1 1
2x 1 !x 1 2
1 5. Let f (x) 5 x and g(x) 5 x2 2 2. What is ( f + g)(23)? B 17 9
17
1 7
29
7
23
Short Response 6. Suppose the function f (x) 5 0.035x represents the number of U.S. dollars
equivalent to x Russian rubles and the function g(x) 5 90x represents the number of Japanese yen equivalent to x U.S. dollars. Write a composite function that represents the number of Japanese yen equivalent to x Russian rubles. Show your work. [2] (g ° f )(x) 5 g(f(x)) 5 90(0.035x) 5 3.15x [1] appropriate method but with one computational error [0] incorrect answer and no work shown OR no answer given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
57
Name
6-6
Class
Date
Enrichment Function Operations
Composition and Linear Functions Two functions f (x) and g(x) are equal if they have the same domains and the same value for each point in their domain. Suppose that f (x) 5 Ax 1 B and g(x) 5 Cx 1 D are two linear functions both of whose domains are the set of real numbers. 1. If f (x) 5 g(x), what can you conclude by examining the values of f and g at x 5 0? B 5 D 2. Use your conclusion to eliminate D from the definition of g(x). g(x) 5 Cx 1 B 3. What equation results from examining the values of f and g at x 5 1? A 1 B 5 C 1 B 4. What can you conclude about A and C? A 5 C 5. When are two linear functions equal? when the coefficients of x are equal and the constant are equal 6. Compute (g + f )(x). ACx 1 BC 1 D 7. What type of function is the composite of two linear functions? linear 8. What is the coefficient of x in the expression for (g + f )(x)? AC 9. What is the constant term? BC 1 D 10. Compute ( f + g)(x) and express it in slope-intercept form. ACx 1 AD 1 B 11. What equation must be satisfied if f + g 5 g + f ? BC 1 D 5 AD 1 B 12. What equations must be satisfied if f + g 5 f ? AC 5 A and AD 1 B 5 B 13. What equations must be satisfied if f + g 5 g ? AC 5 C and AD 1 B 5 D 14. What must occur if f + g 5 0? AC 5 0 and AD 1 B 5 0 15. Constant functions are a subset of linear functions in which the coefficient of x is zero. What type of function is the composite of two constant functions? constant 16. a. If h(x) and k(x) are two constant functions, under what circumstances does h + k 5 k + h? if h(x) 5 k(x) b. Under what circumstances does h + k 5 k? if h(x) 5 k(x) c. Under what circumstances does h + k 5 h? h ° k always equals h d. Under what circumstances does h + k 5 0? if h(x) 5 0
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
58
Name
6-6
Class
Date
Reteaching Function Operations
When you combine functions using addition, subtraction, multiplication, or division, the domain of the resulting function has to include the domains of both of the original functions. Problem
Let f (x) 5 x2 2 4 and g(x) 5 !x. What is the solution of each function operation? What is the domain of the result? a. ( f 1 g)(x) 5 f (x) 1 g(x) 5 (x2 2 4) 1 (!x) 5 x2 1 !x 2 4 b. ( f 2 g)(x) 5 f (x) 2 g(x) 5 (x2 2 4) 2 (!x) 5 x2 2 !x 2 4 c. (g 2 f )(x) 5 g(x) 2 f (x) 5 (!x) 2 (x2 2 4) 5 2x2 1 !x 1 4 d. ( f ? g)(x) 5 f (x) ? g(x) 5 (x2 2 4)(!x) 5 x2 !x 2 4 !x
The domain of f is all real numbers. The domain of g is all x $ 0. For parts a2d, there are no additional restrictions on the values for x, so the domain for each of these is x $ 0. f f (x) (x2 2 4) !x x2 2 4 e. g (x) 5 5 5 x g(x) !x
As before, the domain is x $ 0. But, because the denominator cannot be zero, eliminate any values of x for which g(x) 5 0. The only value for which !x 5 0 is x 5 0. Therefore, f the domain of g is x . 0. f.
g g(x) !x (x) 5 5 2 f f(x) x 24
Similarly, begin with x $ 0 and eliminate any values of x that make the denominator g f(x) zero: x2 2 4 5 0 when x 5 22 and x 5 2. Therefore, the domain of f is x $ 0 combined with x 2 22 and x 2 2. In other words, the domain is x $ 0 and x 2 2, or all nonnegative numbers except 2.
Exercises Let f (x) 5 4x 2 3 and g(x) 5 x2 1 2. Perform each function operation and then find the domain of the result. 1. ( f 1 g)(x)
2. ( f 2 g)(x)
x2
1 4x 2 1; all real numbers
4. ( f · g)(x) 4x3 2 3x2 1 8x 2 6; all real numbers
2x2
1 4x 2 5; all real numbers f 5. g (x) 4x 2 3 ; x2 1 2
all real numbers
3. (g 2 f )(x) x2 2 4x 1 5; all real numbers g 6. (x) f x2 1 2 4x 2 3 ;
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
59
x u 34
Name
Class
6-6
Date
Reteaching (continued) Function Operations
• One way to combine two functions is by forming a composite. • A composite is written (g + f ) or g( f (x)). The two different functions are g and f. • Evaluate the inner function f (x) first. • Use this value, the first output, as the input for the second function, g(x). Problem
What is the value of the expression g( f (2)) given the inner function, f (x) 5 3x 2 5 and the outer function, g(x) 5 x2 1 2? 1st input x ⫽ 2
f(x)
1st output, 1, becomes 2nd input
3x ⫺ 5 3(2) ⫺ 5
g(x) x2
2nd output
⫹ 2
3
12 ⫹ 2
6 ⫺ 5
1 ⫹ 2
1 1st output
3 2nd output
Exercises Evaluate the expression g( f (5)) using the same functions for g and f as in the Example. Fill in blanks 7–14 on the chart. Use one color highlighter to highlight the first input. Use a second color to highlight the first output and the second input. Use a third color to highlight the second output, which is the answer. 1st input x ⫽ 5
f(x)
1st output,
3x ⫺ 5 10. 5) ⫺ 5 7. 3(—
10 , ——— becomes 2nd input
g(x) x2
2nd output
⫹2 14.
102 ———
2 11. 10 — ⫹2
8. 15 — ⫺ 5
12. 100 —⫹2
10 9. ———
102 13. ———
Given f (x) 5 x2 1 4x and g(x) 5 2x 1 3, evaluate each expression. 15. f (g(2)) 77
16. g( f (2.5)) 35.5
17. g( f (25)) 13
18. f (g(25)) 21
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
60
Name
Class
6-7
Date
Additional Vocabulary Inverse Relations and Functions
Choose the word or phrase from the list that best matches each sentence. inverse relation 1. In a
inverse function
one-to-one function
f21
one-to-one function
, each y-value in the range corresponds to exactly one x-value in the domain.
2. A relation pairs element a of its domain to element b of its range. The
inverse relation
pairs b with a. f21
3. The inverse of a function f is represented by
. inverse functions
4. If a relation and its inverse are functions, then they are y
.
5. Circle the inverse of y 5 2x 1 1.
y 5 x 2 12
x5222
1 y5x2 2
6. Circle the inverse of y 5 (3 2 x)2.
y 5 3 1 !x
y 5 3 2 !x
y 5 9 2 !x
7. Circle the inverse of y 5 5x2 1 4.
4 y5x2 5
y 5 "x 2 45
4 y 5 "x 2 5
8. Explain each of the steps followed to find f 21 of f (x) 5 !3x 2 2.
y 5 !3x 2 2
Replace f (x) with y.
x 5 !3y 2 2
Switch x and y.
x2 5 3y 2 2
Square both sides.
x2 1 2 5 3y
Add 2 to both sides.
2 y 5 x 31 2
Divide both sides by 3 and solve for y.
9. Find f21 for f(x) 5 4x 2 8, and explain the steps.
y 5 4x 2 8
Replace f (x) with y.
x 5 4y 2 8
Switch x and y.
x 1 8 5 4y
Add 8 to both sides.
y 5 4x 1 2
Divide both sides by 4 and solve for y.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
61
Name
Class
6-7
Date
Think About a Plan Inverse Relations and Functions
Geometry Write a function that gives the length of the hypotenuse of an isosceles right triangle with side length s. Evaluate the inverse of the function to find the side length of an isosceles right triangle with a hypotenuse of 6 in.
Know 1. An equation that relates the length of each side s and the
length of the hypotenuse h of an isosceles right triangle is 2 5 h2 z . z 2s
s
h
Need 2. To solve the problem I need to: write a function for the length of the hypotenuse in
s
of the side length and then find the inverse function for the side length in of the hypotenuse
.
Plan 3. A function that gives the length of the hypotenuse h in of the side length
z
z
s is h 5 s"2 .
4. An inverse function that gives the side length s in of the length of the
hypotenuse h is
s5 h "2
.
5. What is the value of the inverse function for h 5 6 in.? about 4.24 in.
6. Is the side length reasonable? Explain. Yes; the side length is less than the length of the hypotenuse
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
62
.
Name
Class
Date
Practice
6-7
Form G
Inverse Relations and Functions
Find the inverse of each relation. Graph the given relation and its inverse. 1.
3.
2.
4 y
x
22 21
0
1
y
23 22 21
0
x
23
22
21
0
y
22
21
0
1
x
23
21
1
2
y
21
0
1
3
2 2
21
0
1
3
y
23
21
1
2
4.
y 2
0
1
2
3
23 21
0
22
y 2 ⫺2
4
⫺4
⫺2
x
y
x
⫺4
x
x
x
23
21
0
22
y
0
1
2
3
x
23
22
21
0
y
3
2
1
0
x
3
2
1
0
y
23
22
21
0
2 ⫺2
4 y 2
2 ⫺2
⫺2 ⫺2 ⫺4
Find the inverse of each function. Is the inverse a function? 5. y 5 x2 1 2 y 5 w!x 2 2; no
6. y 5 x 1 2
8. y 5 2x2 2 3 y 5 w!2x 2 3; no
9. y 5 2x 2 1
11. y 5 5x2 y 5 w"x5; no
14. y 5 3x2 2 2
2 y 5 w"x 1 3 ; no
7. y 5 3(x 1 1)
y 5 x 2 2; yes y5
1 2x
1
1 2;
y 5 13 x 2 1; yes 10. y 5 1 2 3x2
yes
x y 5 w"1 2 3 ; no
12. y 5 (x 1 3)2 y 5 w!x 2 3; no
13. y 5 6x2 2 4
15. y 5 (x 1 4)2 2 4 y 5 w!x 1 4 2 4; no
16. y 5 2x2 1 4 y 5 w!4 2 x; no
4 y 5 w"x 1 6 ; no
Graph each relation and its inverse. 17. y 5
x13 3 6 4 2
1 18. y 5 2 x 1 5
y x
⫺4 O 2 4 6
1 20. y 5 2 x2 3 2 1 ⫺3⫺2 O ⫺2 ⫺3
19. y 5 2x 1 5 y
y 6 4 2 O ⫺6⫺4⫺2 2 ⫺2 ⫺4 ⫺6
6
x
21. y 5 (x 1 2)2 y x 1 2 3
2 O ⫺6⫺4⫺2 4 ⫺2 ⫺4 ⫺6
y
4 ⫺4 O ⫺4
x
22. y 5 (2x 2 1)2 2 2
y 2 4
x
⫺6 ⫺2 4 6
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
63
x
x 2
x 2
4
Name
6-7
Class
Date
Practice (continued)
Form G
Inverse Relations and Functions
For each function, find the inverse and the domain and range of the function and its inverse. Determine whether the inverse is a function. 1 23. f (x) 5 6 x f 21(x) 5 6x; 24. The domain and range of f and f 21 is the set of all real numbers; f 21 is a function.
f (x) 5 215 x 1 2
25. f (x) 5 x2 2 2 f 21(x) 5 w!x 1 2; 5 25x 1 10; The Domain of f 5 all real numbers 5 range domain and range of f and of f 21; Range of f 5 the set of real 21 f is the set of all real numbers greater than or equal to 22 5 numbers; f 21 is a function. domain of f 21; f 21 is not a function.
26. f (x) 5 x2 1 4 f 21(x) 5 27. w!x 2 4; Domain of f 5 all real numbers 5 range of f 21 ; Range of f 5 all real numbers greater than or equal to 4 5 domain of f 21 ; f 21 is not a function. 29. f (x) 5 3 2 x 30. 21 f (x) 5 3 2 x; the domain and range of f and f 21 is the set of all real numbers; f 21 is a function.
f (x) 5 !x 2 1 f 21(x) 5 28. f (x) 5 !3x f 21(x) 5 13 x2 ; The
f 21(x)
x2 1 1; Domain of f 5 all real numbers greater than or equal to 1 5 range of f 21 ; Range of f 5 all real numbers greater than or equal to 0 5 domain of f 21 ; f 21 is a function. f (x) 5 (x 1 1)2 f 21(x) 5 31. 21 6 !x ; domain f 5 all real numbers 5 range f 21 ; range f 5 all nonnegative real numbers 5 domain f 21 ; f 21 is not a function.
domain and range of f and f 21 is the set of all real numbers greater than or equal to 0; f 21 is a function.
f (x) 5
1 !x
f 21(x) 5 12 ; the domain and x range of f and f 21 is the set of all positive real numbers; f 21 is a function.
32. The equation f (x) 5 198,900x 1 635,600 can be used to model the number of
utility trucks under 6000 pounds that are sold each year in the U.S. with x 5 0 representing the year 1992. Find the inverse of the function. Use the inverse to estimate in which year the number of utility trucks under 6000 pounds sold in the U.S. will be 6,000,000. Source: www.infoplease.com f 21(x) 5
x 2 635,600 198,900
in 2019
33. The formula s 5 0.04n 1 2500 gives an employee’s monthly salary s, in
dollars, after selling n dollars in merchandise at an appliance store. a. Find the inverse of the function. Is the inverse a function? n 5 25s 2 62,500; yes b. Use the inverse to find the amount of merchandise sold if the employee’s salary was $2820 last month. $8000
34. The formula for the surface area A of a sphere of radius r is A 5 4pr2 for r $ 0. A a. Find the inverse of the formula. Is the inverse a function? r 5 "4p ; yes b. Use the inverse to find the radius of a sphere with surface area 10,000 m3. 28.2 m
Let f (x) 5 2x 1 5. Find each value. 35. ( f 21 + f )(21) 21
36. ( f + f 21)(3) 3
1 1 37. ( f + f 21) Q 22 R 22
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
64
Name
Class
Date
Practice
6-7
Form K
Inverse Relations and Functions
Find the inverse of each relation. Graph the given relation and its inverse. 1.
x
y
0
2.
x
y
21
22
1
1
2 3
x 21 1 3 5
3.
x
y
7
23
2
0
3
22
2
3
2
7
21
2
5
4
19
0
2
y 0 1 2 3
6
y
x 7 3 7 19
4 2 O
x 2
4
6
y 22 0 2 4
15
y
x 2 2 2 2
10 5 O
x 5 10 15
4 y
y 23 22 21 0
⫺4 ⫺2 O ⫺2 ⫺4
Find the inverse of each function. Is the inverse a function? To start, switch x and y. x 4. y 5 2 y x 5 2 y 5 2x; yes
5. y 5 x2 1 4
6. y 5 (3x 2 4)2
y 5 w!x 2 4; no
y5w
!x 1 4 ; 3
no
Graph each relation and its inverse. 8. y 5 2x2
7. y 5 3x 2 4 4 y
4 y
2 ⫺4 ⫺2 O ⫺2 ⫺4
9. y 5 (3 2 2x)2
x 2
4
2 ⫺2 ⫺2
y 6
O 2
x 4
4 2 O
⫺4
2
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
65
4
6 x
x 4
Name
Class
6-7
Date
Practice (continued)
Form K
Inverse Relations and Functions
Find the inverse of each function. Is the inverse a function? 10. f (x) 5 (x 1 1)2 y 5 w!x 2 1; no
2x3 11. f (x) 5 5
12. f (x) 5 !3x 1 4
y 5 3Å52 x; yes
y5
(x 2 4) 2 ; 3
yes
13. Multiple Choice What is the inverse of y 5 5x 2 1? B
f 21(x) 5 5x 1 1
f 21(x) 5
x11 5
x
x
f 21(x) 5 5 1 1
f 21(x) 5 5 2 1
For each function, find its inverse and the domain and range of the function and its inverse. Determine whether the inverse is a function. 14. f (x) 5 !x 1 1 15. f (x) 5 10 2 3x 16. f (x) 5 4x2 1 25 10 1 21 2 21 !x 2 25 f (x) 5 x 2 1; domain f (x) 5 23 x 1 3 ; domain f21(x) 5 w ; domain 2 f(x): x L 21, range f(x): all real numbers; range f(x): all real numbers; f(x): y L 0; domain f 21 : range f(x): y L 25; domain f(x): all real numbers; x L 0, range f 21 : y L 21; 21 : all real domain f f 21: x L 25; range f 21 : all the inverse is a function. numbers; range f 21 : all real real numbers; the inverse is numbers; the inverse is a not a function. function. 17. The formula for the area of a circle is A 5 pr2 . a. Find the inverse of the formula. Is the inverse a function? r 5 ÅA p ; yes b. Use the inverse to find the radius of a circle that has an area of 82 in.2. about 5.1 in.
For Exercises 18−20, f (x) 5 5x 1 11. Find each value. To start, rewrite f (x) as y and switch x and y. 18. A f f 21 B(5)
19. A f 21 f B(23)
°
°
y 5 5x 1 11 5
20. A f 21 f B(0)
°
0
23
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
66
Name
Class
6-7
Date
Standardized Test Prep Inverse Relations and Functions
Multiple Choice For Exercises 1−4, choose the correct letter. 1. What is the inverse of the relation?
x y
y
22 21 3
0
2
A
1 21 22
3
x
22 21
0
2
0 21 22
y
22 21
1
3
22 21
1
22 21 2
x
x
⫺2 ⫺1
0
2
x
y
⫺3 ⫺1
1
2
y
2
1
3
1 21 22
2. What is the inverse of the function? y 5 5(x 2 3) G
y5
x13 5
y 5 15 x 1 3
y 5 5(x 1 3)
y 5 15 x 2 3
3. What function with domain x $ 5 is the inverse of y 5 !x 1 5? C
y 5 x2 1 5
y 5 x2 2 5
y 5 (x 2 5)2
y 5 (x 1 5)2
4. What is the domain and range of the inverse of the function? y 5 !x 2 5 F
domain is the set of all real numbers $ 0; range is the set of all real numbers $ 5 domain is the set of all real numbers $ 5; range is the set of all real numbers $ 0 domain and range is the set of all real numbers $ 5 domain and range is the set of all real numbers
Extended Response 5. A high school principal uses the formula y 5 150x 1 180 to predict a
student’s score on a state achievement test using the student’s 11th-grade GPA number x. a. What is the inverse of the formula? b. Is the inverse a function? c. Using the inverse, what GPA does a student need to get a ing score of 510 on the state exam? 1 1 [4] a. y 5 150 (x 2 180) or y 5 150 x 2 65 b. yes c. 2.2 [3] most work is correct but there are minor errors [2] student understands the problem and shows some correct work [1] student may understand the problem but doesn’t know how to proceed OR correct answers without work shown [0] no answers given
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
67
Name
6-7
Class
Date
Enrichment Inverse Relations and Functions
Composition, Inverses, and Linear Functions Solving an equation for one variable in of another is an important step in finding inverses. This step is also used in conversion formulas. Consider the following linear functions. Let F denote the temperature in degrees Fahrenheit, C the temperature in degrees Celsius, and K the temperature in degrees Kelvin. The formula for converting degrees Fahrenheit to degrees Celsius is C 5 59 (F 2 32), and the formula for converting degrees Celsius to degrees Kelvin is K 5 C 1 273. 1. Use composition to determine the formula for converting degrees Fahrenheit
to degrees Kelvin. K 5 5(F 2 32) 1 273 9 2. Solve this function for F. F 5 95 (K 2 273) 1 32 3. This new equation converts degrees
Kelvin
to degrees Fahrenheit .
9 4. Derive a formula to convert degrees Celsius to degrees Fahrenheit. F 5 5C 1 32
5. Derive a formula to convert degrees Kelvin to degrees Celsius. C 5 K 2 273 6. Compose these two functions to find a formula for converting degrees Kelvin to degrees Fahrenheit. F 5 95 (K 2 273) 1 32
Solve each of the following problems involving functions. 7. In 1940, the cost of a new house was $10,000. By 1980, this cost had risen to
$90,000. Assuming that the increase is linear, find a function expressing the cost c of a new house in of the year y. Solve this function for y. What does this new function enable you to do? c 2 10,000
c 5 10,000 1 2000( y 2 1940); y 5 2000 1 1940; find the year given the cost of a house 8. Between the ages of 5 and 15, a typical child grows at a fixed annual rate. If Mary
was 42 in. in height when she was 5 yr old and grew at a rate of 2 in. a year, find a formula that expresses Mary’s height h in inches when her age is a years. Solve this function for a. What does this new function enable you to do?
h 5 2(a 2 5) 1 42; a 5 h 22 42 1 5; compute Mary’s age given her height 9. The air temperature, in degrees Fahrenheit, surrounding an airplane on one
1 particular day was modeled by T 5 2200 a 1 110, where a is the altitude, in feet, of the airplane. Solve this function for a. What does this new function enable you to do?
a 5 200(2T 1 110); find the altitude of the airplane given the temperature 10. The formula L 5 0.25W 1 0.5 models the length of a certain spring, in inches,
when a weight of W ounces is attached to it. Solve this function for W. What does this new function enable you to do? 2 0.5 W 5 L 0.25 ; find the weight attached to the spring given the length of the stretched spring
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
68
Name
Class
Date
Reteaching
6-7
Inverse Relations and Functions
•
Inverse operations “undo” each other. Addition and subtraction are inverse operations. So are multiplication and division. The inverse of cubing a number is taking its cube root.
•
If two functions are inverses, they consist of inverse operations performed in the opposite order.
Problem
What is the inverse of the relation described by f (x) 5 x 1 1? f (x) 5 x 1 1 y5x11
Rewrite the equation using y, if necessary.
x5y11
Interchange x and y.
x215y
Solve for y.
y5x21
The resulting function is the inverse of the original function.
So, f 21 (x) 5 x 2 1.
Exercises Find the inverse of each function. 2. y 5 3x3 1 2
1. y 5 4x 2 5 f 21 5
x 1 5 4
f 21 5
4. y 5 0.5x 1 2 f 21
5 2x 2 4
x 7. f (x) 5 5 f 21(x) 5 5x
3. y 5 (x 1 1)3
3 2 "x 2 3
3
f 21 5 "x 2 1
5. f (x) 5 x 1 3 f 21(x) 5 x 2 3
6. f (x) 5 2(x 2 2)
8. f (x) 5 4x 1 2
9. y 5 x
f 21(x)
4 f 21(x) 5 x 1 2
x22 4
5 x21 10. y 5 x 2 3 11. y 5 2 f 21 5 x 1 3 f 21 5 2x 1 1 2 13. f (x) 5 !x 1 2 14. f (x) 5 3 x 2 1 f 21(x) 5 32(x 1 1) f21 (x) 5 x2 2 2 for x L 22 16. f (x) 5 2(x 2 5)2 f 21(x)
556
"x2
17. y 5 !x 1 4 f 21
5 (x 2
4)2
f 21 5 x 12. y 5 x3 2 8 3
f 21 5 "x 1 8
x13 5 f 21(x) 5 5x 2 3
15. f (x) 5
18. y 5 8x 1 1 for x L 0
1 f 21 5 x 2 8
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
69
Name
6-7
Class
Date
Reteaching (continued) Inverse Relations and Functions
Examine the graphs of f (x) 5 !x 2 2 and its inverse, f 21(x) 5 x2 1 2, at the right.
6 5 4 3 2 1
Notice that the range of f and the domain of f 21 are the same: the set of all real numbers x $ 0. Similarly, the domain of f and the range of f 21 are the same: the set of all real numbers x $ 2.
y
f ⫺1
f x
O
1 2 3 4 5 6
This inverse relationship is true for all relations whenever both f and f 21 are defined. Problem
What are the domain and range of the inverse of the function f (x) 5 !3 2 x? f is defined for 3 2 x $ 0 or x # 3. Therefore, the domain of f and the range of f 21 is the set of all x # 3. The range of f is the set of all x $ 0. So, the domain of f 21 is the set of all x $ 0.
f
6 5 4 3 2 1
23 22 21 O
Exercises
y
x 1 2 3
Name the domain and range of the inverse of the function. 1 19. y 5 2x 2 1 20. y 5 2 2 x The domain and the range is domain: x u 2; the set of all real numbers. range: y u 0
21. y 5 !x 1 5 domain: x L 0; range: y L 25
22. y 5 !2x 1 8 domain: x L 8; range: y K 0
23. y 5 3 !x 1 2 domain: x L 2; range: y L 0
24. y 5 (x 2 6)2 domain: x L 0; range: all real numbers
25. y 5 x2 2 6
1 26. y 5 x 1 4
27. y 5
domain: x L 26; range: all real numbers
domain: x u 0; range: y u 24
1 (x 1 4)2 domain: x S 0; range: y u 24
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
70
Name
6-8
Class
Date
Additional Vocabulary Graphing Radical Functions
1. Circle the radical functions in the group below.
y 5 2(x 1 5) 2 3
y 5 22 !x 2 4
y5x24
3 y5 ! x18
2. Circle the square root functions in the group below. 3 y5 ! x22
y 5 !x 1 4
y 5 2 !x 2 3
y 5 3(x 1 6)
For Exercises 3−8, draw a line from each word or phrase in Column A to its matching item in Column B. Column A
Column B
3. parent function
A. y 5 !x 2 k
4. translate k units downward
B. y 5 2!x
5. stretch vertically by the factor k (k . 1)
C. y 5 !x 2 k
6. translate k units upward
D. y 5 !x
7. reflection in x-axis
E. y 5 k !x
8. translate k units to the right
F. y 5 !x 1 k
Identify the meaning of the following in the function y 5 2!x 2 4 1 5. 9. 2:
Stretch vertically by a factor of 2
.
10. 4:
Translate 4 units to the right
.
11. 5:
Translate 5 units upward
.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
71
Name
6-8
Class
Date
Think About a Plan Graphing Radical Functions
Electronics The size of a computer monitor is given as the length of the screen’s 5 diagonal d in inches. The equation d 5 6 !3A models the length of a diagonal of a monitor screen with area A in square inches.
a. Graph the equation on your calculator.
b. Suppose you want to buy a new monitor that has twice the area of your old
monitor. Your old monitor has a diagonal of 15 inches. What will be the diagonal of your new monitor?
1. How can you use a graph to approximate the area of the old monitor? Graph the equation and graph y 5 15. The x-coordinate of their intersection will be the area of the old monitor
.
2. Graph the equation on your calculator. Make a sketch of the
graph.
d 40 30
3. What is the area of the old monitor? 108 in.2
4. How can you check your answer algebraically?
20 10 0
0
100 200 300 400
Substitute 15 for d and solve the equation for A
A
.
5. Show that your answer checks. 15 5 56"3A, 15 Q 65 R 5 "3A, 18 5 "3A, 182 5 3A, 324 5 3A, A 5 108 6. How can you find the diagonal of a new monitor with twice the area of the old
monitor? Substitute 2 times the area of the old monitor for A in the equation
7. Use your method to find the diagonal of your new monitor. d55 "3A 5 56"3 ? 2 ? 108 5 56"648 N 21.2 in. 6 8. What will be the diagonal of your new monitor? about 21.2 in.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
72
.
Name
Class
Date
Practice
6-8
Form G
Graphing Radical Functions
Graph each function. 1. y 5 !x 1 3
2. y 5 !x 2 1
8 y 6 4 2
6 y
4
4
2 x
O
2
4
6
4. y 5 !x 2 3
O ⫺2 ⫺6 ⫺4 ⫺8
2
x 4 6 8
2
4 6
2
2
1 6. y 5 4 !x 2 1 1 5
y
4
x
⫺4 ⫺2 O ⫺2
5. y 5 22 !x 2 2
6 y
O
1
x 2 4 6 8
O ⫺2
8
3. y 5 !x 1 5
6 y
8 6 4 2
x
y
O
x 2 4 6 8
Solve each square root equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 7. !x 1 6 5 9 75
no solution; 32 9. !3x 2 5 5 !1 2 x is extraneous
8. !4x 2 3 5 5 7
r
A 10. If you know the area A of a circle, you can use the equation r 5 to find Äp the radius r. a. Graph the equation. b. What is the radius of a circle with an area of 350 ft2? about 10.6 ft
12 8 4 A
Graph each function. 3
3
y
O ⫺2
13. y 5 !x 1 3 2 1
2 2
x
⫺2
O
2 2
x
⫺4
⫺2
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
73
100
y
y
2 ⫺2
3
12. y 5 2 !x 2 3
11. y 5 2!x 1 2
O
⫺2
O ⫺2
2 x
200
300
Name
6-8
Class
Date
Practice (continued)
Form G
Graphing Radical Functions
Rewrite each function to make it easy to graph using transformations of its parent function. Describe the graph. 14. y 5 !81x 1 162
15. y 5 2!4x 1 20
y 5 9 !x 1 2; graph of y 5 9 !x shifted left 2 units 17. y 5 2!64x 1 192
y 5 22 !x 1 5; graph of y 5 22 !x shifted left 5 units 3
18. y 5 2!8x 2 56 1 4
y 5 28 !x 1 3; graph of y 5 28 !x shifted left 3 units 20. y 5 !0.25x 1 1
3
16. y 5 !125x 2 250 3 y 5 5 !x 2 2; graph of 3 y 5 5 !x shifted right 2 units
19. y 5 !25x 1 75 2 1
y 5 5 !x 1 3 2 1 ; graph of y 5 5 !x shifted left 3 units
3
y 5 22 !x32 7 1 4 ; graph of y 5 22 !x shifted right 7 units and up 4 units 21. y 5 5 2 !4x 1 2
y 5 0.5 !x 1 4; graph of y 5 0.5 !x shifted left 4 units
y 5 5 2 2"x 1 12; graph of y 5 22 !x shifted left 12 unit and up 5 units
and down 1 unit 3
22. y 5 !27x 2 54 3 y 5 3 !x 2 2; graph of 3 y 5 3 !x shifted right 2 units
3 3V 23. To find the radius r of a sphere of volume V, use the equation r 5 Å 4p . a. Graph the equation. b. A balloon used for advertising special events has a volume of 225 ft3. What is the radius of the balloon? 3.77 ft
24. An exercise specialist has studied your exercise routine and says the
formula t 5 1.85 !c 1 10 expresses the amount of time t, in minutes, it takes you to burn c calories (cal) while exercising. a. Graph the equation. b. According to this formula, how long should it take you to burn 100 cal? 200 cal? 300 cal? 19.4 min, 26.8 min, 32.6 min 25. You can use the equation t 5
1 4 !d
to find the time t, in seconds, it takes an object to fall d feet after being dropped. a. Graph the equation. b. How long does it take the object to fall 400 feet? 5 s
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
74
5 4 3 2 1
r
V O 100 300 500 50 40 30 20 10
t
O 100 10 t 8 6 4 2 O 200
c 400
d 800
Name
Class
Date
Practice
6-8
Form K
Graphing Radical Functions
Graph each function. 1. y 5 !x 1 3 6
2. y 5 !x 2 4
y
6
4
3. y 5 !x 2 7
y
y O ⫺2
4
2
2
x
O
2
4
x
O
6
2
4
6
x 2
4
6
⫺4 ⫺6
Graph each function. 4. y 5 4 !x 6
5. y 5 22 !x 1 1
y
y
4
O ⫺2
2
⫺4
x
O
2
4
x 2
4
6
4 y 2 O ⫺2
⫺6
6
6. y 5 5 !x 2 4
x 2
4
6
⫺4
Solve each square root equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 7. !x 1 2 5 7 47 8 6 4 2 O
y
8. !4x 1 1 5 5 6 6
9. 3 !3 2 x 5 10 28.11 y
y 9
4 x 10 20 30 40
6
2 O
x 2
4
6
3
10. A periscope on a submarine is at a height h, in feet, above the surface of the water. The
greatest distance d, in miles, that can be seen from the periscope on a clear day is given 3h
by d 5 Å 2 . a. If a ship is 3 miles from the submarine, at what height above the water would the submarine have to raise its periscope in order to see the ship? 6 ft b. If a ship is 1.5 miles from the submarine, to what height would it have to be raised? 1.5 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
75
Name
Class
Date
Practice (continued)
6-8
Form K
Graphing Radical Functions
3 Graph each function. To start, graph the parent function, y 5 ! x. 3
1 3 13. y 5 2 !x 2 1 1 3
3
12. y 5 3 2 !x 1 1
y
y 6
y 6
4
4
11. y 5 !x 2 4 ⫺2 ⫺2
x
2
⫺4 ⫺6
⫺2
2
x
⫺2
x
2
14. A center-pivot irrigation system can water from 1 to 130 acres of crop land.
The length l in feet of rotating pipe needed to irrigate A acres is given by the function l 5 117.75!A. a. Graph the equation on your calculator. Make a sketch of the graph. b. What length of pipe is needed to irrigate 40, 80, and 130 acres? 744.7 ft, 1053.2 ft, 1342.6 ft
300
y
200 100 ⫺4 ⫺2 O
Graph each function. Find the domain and range. 3
3
15. y 5 2 !x 2 4
16. y 5 2!8x 1 5 y
4 y 2 O
12 8 4
x 2
4
6
⫺2 O ⫺8
2
x
domain: all real numbers; range: all real numbers
domain: all real numbers; range: all real numbers
17. y 5 23 !x 2 4 2 3 y 4 2 O 4 ⫺2 2 ⫺4 ⫺6 ⫺8
x 6 8
domain: x L 4; range: y K 23
18. Open Ended Write a cube root function in which the vertical translation of 3 y5 ! x is twice the horizontal translation. Answers may vary. Any cube root 3
function in the form y 5 a !x 2 h 1 k where k 5 2h.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
76
x 2
4
Name
Class
Date
Standardized Test Prep
6-8
Graphing Radical Functions
Multiple Choice For Exercises 1−4, choose the correct letter. 1. What is the graph of y 5 !x 1 4? C 8 6 4
y
x ⫺4⫺2 O
2 4
8 6 4 2 O
y
x 2 4 6 8
8 6 4 2
y
8 6 4
y
x
x ⫺4⫺2 O
2 4 6 8
O
2 4
2. What is the graph of y 5 !x 2 3 2 2? F y
y 4 2
1 O
8x
2 4
⫺2 ⫺3
⫺4
2 4 x
⫺2 ⫺4
6 4 2 O
y x 2 4 6 8
⫺4
8 6 4 2 O
y
x 2 4 6 8
3 3. What is the graph of y 5 1 2 !x 1 3? D
4 ⫺6⫺4⫺2 ⫺2 ⫺4
y x O
4 2 ⫺4⫺2 ⫺2 ⫺4
y x 2 4
4 2
y
⫺8⫺6⫺4⫺2 O x ⫺4
y
4 2
x
⫺6⫺4⫺2 ⫺2 ⫺4
2
4. What is the description of y 5 !9x 2 3 to make it easy to graph using transformations of its parent function? G
the graph of y 5 3 !x, shifted right 3 units the graph of y 5 3 !x, shifted right 13 unit the graph of y 5 !x, shifted right 3 units and up 9 units the graph of y 5 !x, shifted right 13 unit and up 9 units
6 y 4
Short Response
2
5. What is the graph of y 5 2 !x 2 1 1 3?
O
[2] The graph is correct. [1] One of the transformations (horizontal, vertical, or stretch) is incorrect. [0] no answer given Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
77
x 2
4
6
Name
Class
Date
Enrichment
6-8
Graphing Radical Functions
Transformations of Other Functions You can obtain the graph of any function of the form y 5 a ? f(x 2 h) 1 k by using the shifting rules similar to those used to obtain the graph of y 5 a!x 2 h 1 k. Note that the second function is a special case of the first when f(x) 5 !x. To obtain the graph of y 5 a ? f(x 2 h) 1 k, given the graph of y 5 f(x), use the following general rules: • If a , 0, reflect the graph of y 5 f(x) across the x-axis. • If ua u . 1, the graph of y 5 f(x) is stretched by a factor of a. • If 0 , ua u , 1, the graph of y 5 f(x) is compressed by a factor of a. • The graph of y 5 f(x) is shifted right h units if h . 0 and left h units if h , 0. • The graph of y 5 f(x) is shifted up k units if k . 0 and down k units if k , 0. 1. Use the general rules to describe how the graph of y 5 23(x 2 5)2 1 7 can
be obtained from the graph of f(x) 5 x2 . reflect across the x-axis, stretch by a factor of 3, shift right 5 units and shift up 7 units 3
2. Write the equation for the graph that looks like y 5 !x but that is shifted
right four units, reflected across the x-axis, and shifted down six units. 3
y 5 2!x 2 4 2 6 3. Use the graph of y 5 f(x) given below to sketch the graph of y 5 f(x 1 2) 2 1. y
6 4 2
y ⴝ f (x)
4
x ⫺4
O
4
⫺6 ⫺4 ⫺2 O
⫺4
y
y 4 x 2 4 6
⫺4 ⫺6
x O
⫺4
4
⫺4
4. The graph of y 5 f(x) and y 5 g(x) is given below. The graph of g is a transformation of the graph of f. Write the equation for the graph of g in of f. g(x) 5 f(x 1 1) 23 y f
2
x
O ⫺2
2 ⫺2 g
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
78
Name
Class
6-8
Date
Reteaching Graphing Radical Functions
The graph of y 5 a!x 2 h 1 k is a translation h units horizontally and k units vertically of y 5 a!x. The value of a determines a vertical stretch or compression of y 5 !x. Problem 6
What is the graph of y 5 2 !x 2 5 1 3?
y
4
y 5 2 !x 2 5 1 3
2 x
a52
O
h55 k53
2
4
6
Translate the graph of y 5 2 !x right five units and up three units. The graph of y 5 2 !x looks like the graph of y 5 !x with a vertical stretch by a factor of 2.
Exercises Graph each function. 1. y 5 !x 2 4 1 1 4 y
2. y 5 !x 2 4
2 O
2
3. y 5 !x 1 1
5. y 5 2 !x 2 1
7. y 5 2!x 1 1
6. y 5 22 !x 1 3 1 4
y 2
2
2 y
8. y 5 !x 1 3 2 4
x
y ⫺4 ⫺2 O ⫺2
4
⫺4
⫺4 6 y
10. y 5 2!x 2 2
4 2 O
x
⫺4 ⫺2 O
O ⫺2
9. y 5 3 !x 1 2
6 y 4
x
⫺2 O ⫺2
2
4
x
⫺4 ⫺2 O ⫺2
2
2
y
4. y 5 2!x 1 2 2 3 x
⫺2 O ⫺2
2
⫺4
y
2
x
⫺2 O ⫺2
x 6
4
y
x
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
79
x
Name
6-8
Class
Date
Reteaching (continued) Graphing Radical Functions
Graphs can be used to find solutions of equations containing radical expressions. Problem
What is the minimum braking distance of a bicycle with a speed of 22 mph? You can find the minimum braking distance d, in feet, of a bicycle travelling s miles per hour using the equation s 5 5.5 !d 1 0.002 . We want to find the value of d when s 5 22. In other words, solve the equation 5.5 !d 1 0.002 5 22. Graph Y1=5.5√(X+0.002) and Y2=22. Try different values until you find an appropriate window. Then use the intersect feature to find the coordinates of the point of intersection.
Intersection x ⫽ 15.998 Y ⫽ 22
The minimum braking distance will be about 16 ft.
Exercises Solve the equation by graphing. Round the answer to the nearest hundredth, if necessary. If there is no solution, explain why. 11. !3x 1 1 5 5 8
12. !4x 1 1 5 9 20
13. !2 2 5x 5 4 22.8
14. !3x 1 5 5 7 14.67
15. !7x 1 2 5 11 17
16. !2x 2 1 5 !1 2 2x 0.5
17. !x 2 2 5 !2 2 3x no solution; x 5 1 is extraneous
18. 7!x 2 3 5 2!2x 1 1 3.68
19. !2x 2 5 5 !4 2 x 3
20. !2x 1 7 5 3!5x 1 2 20.26
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
80
Name
Class
Date
Chapter 6 Quiz 1
Form G
Lessons 6-1 through 6-4 Do you know HOW? Find all the real roots. 1. !36 26, 6
8 4. 3 2 Å 125
3
2. !0.25 20.5, 0.5
3. !264 24
225
Simplify each radical expression. Use absolute value symbols when needed. 2 6. "49x4 7x
5. "25y2 5|y|
2 3 8. " 20.125y6 –0.5y
3 3 7. " 28x9 22x
Find the two real solutions of each equation. 2 2 9. 9x2 2 4 5 0 23, 3
10. x4 5 0.0016 20.2, 0.2
Multiply or divide and simplify. Assume that all variables are positive. 11. 2 !2x ?
3 " 4xy7
"18xy2 12xy
12. 3 "32x4y4
y 2x
Simplify. Rationalize all denominators. 13. 3 !180 1 !45 2 8 !20 5 !5
14.
5 1 !3 2 2 !3
13 1 7 !3
Simplify each expression. 2
15. (2125)3 25
3
17. 320.6 8
16. 814 27
18. 491.5 343
Do you UNDERSTAND? 19. Geometry What is the perimeter of the triangle at the right? 27 2 !2 7
2
2
3 V2
3 V2
20. Reasoning Solve. !75 1 !3x 5 12 !3 49
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
81
5 3 V2
Name
Class
Date
Chapter 6 Quiz 2
Form G
Lessons 6-5 through 6-8 Do you know HOW? Solve. Check for extraneous solutions. 1. !x 2 2 5 x 2 8 11
2. !x 1 4 5 !3x 2 2 3
Let f (x) 5 x2 2 x 2 12 and g (x) 5 x 2 4. Perform each function operation and then find the domain. 3. f (x) 2 2g(x) x2 2 3x 2 4; all real numbers 4. f (x) ? g (x) x3 2 5x2 2 8x 1 48; all real numbers f (x) g (x) 1 x 1 3; x u 4 5. 6. g (x) f (x) x 1 3; x u 4 and x u 23
Let f (x) 5 2x 2 5 and g (x) 5 x2 . Find each composition. 7. ( f + g)(x) 2x2 2 5
8. (g + f )(x) 4x2 2 20x 1 25
Find the inverse of each function. Is the inverse a function? x 3 9. g(x) 5 "2 2 3 g21(x) 5 2x2 1 6, x L 6; 10. h(x) 5 5 2 x3 h21(x) 5 ! 5 2 x; yes yes
Graph. Find the domain and range of each function. 11. y 5 2 2 !x
12. y 5 !x 2 1 1 1
6 y 4
domain: x L 0, range: y K 2
2 O
4
4
domain: x L 1, range: y L 1
x 2
6 y 2 O
6
x 2
4
Do you UNDERSTAND? 13. Writing Explain why it is not true that !22 ? !22 5 !4, even though
(22) ? (22) 5 4. Answers may vary. Sample: !22 ? !22 5 i!2 ? i!2 5 i2(!2)2 5 (21)(2) 5 22 u !4 14. Reasoning Suppose the cost of an item is x dollars. It is marked up by n% and,
later, that new cost is reduced by n%. Is the final cost equal to x dollars? Use a composition of functions to justify your answer. No; answers will vary. Sample: Let n 5 20, then f(x) 5 1.2x and g(x) 5 0.8x and (g f)(x) 5 0.8(1.2x) 5 0.96x.
°
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
82
6
Name
Class
Date
Chapter 6 Test
Form G
Do you know HOW? Simplify each radical expression. Use absolute value symbols when needed. 1. "400x2y6 20»xy3… 3
3
4. " 64a6b2
4a2 "b2
3
4
2. " 2125a9 25a3
4 3. " 81x5y9 3»x…y2 "xy
5. "50s2t4 5»s…t2 !2
6. "256x16y28 16x8y14
Simplify each expression. Rationalize all denominators. Assume that all variables are positive. 7.
"200x3y "2xy5
8. Q 8 2 3 !2 R Q 8 1 3 !2 R 46
10x y2
10. "8x3 ? "2x5 4x4 13.
2 22 1 2 !2 1 1 !2
9.
1 !3 1 5
5 2 !3 22
3
3 3 !2 1 1 !4 1 !2 11. !63 1 2 !28 2 5 !7 2 !7 12. 3 2 !4
4
4 !5 !20 14. 4 2 !4
15. !15 Q 1 2 !45 R !15 2 15 !3
Simplify each expression. Assume that all variables are positive. 16.
16x5y10
Q 81xy2 R
19. Q 4x22y4 R
3 4
2
8x3y6 27 1
22
2
1
17. (264)23 16
x 2y2
20. Q 8ab2 R
1
22
1
7
18. a3 ? a2 a6 1
Q 8ab2 R 2 1
2 1
1 1
9 5
21. Q s5 t3 R Q s2 t2 R s10t6
Solve each equation. Check for extraneous solutions. 3
22. !x 2 3 5 1 4 1
25. (2x 1 1)3 5 3 13
23. !x 1 7 5 x 1 1 2
24. !3x 2 8 5 2 4
26. "x2 2 5 5 4 w"21
27. 3(x 1 1)3 5 48 29, 7
4
Let f(x) 5 x2 1 5 and g(x) 5 x 2 7. Perform each function operation and then find the domain. 2 f (x) x 1 5 ; all real x 27 28. g (x) numbers except 7
29. f (x) 2 2g (x) x2 2 2x 1 19; 30. f (x) ? g(x) all real numbers x3 2 7x2 1 5x 2 35; all real numbers For each pair of functions, find (f + g)(x) and (g + f )(x). 31. f(x) 5 3x 1 5, g(x) 5 x2 1 1
32. f(x) 5 x2 2 5x 1 2, g(x) 5 2x
3x2 1 8; 9x2 1 30x 1 26
4x2 2 10x 1 2; 2x2 2 10x 1 4
33. f(x) 5 !2x 2 1, g(x) 5 5x 1 3 !10x 1 5; 5 !2x 2 1 1 3
34. f(x) 5 22x2, g(x) 5 x 1 4 22x2 2 16x 2 32; 22x2 1 4
Let f(x) 5 5x 2 4 and g(x) 5 x2 2 1. Find each value. 35. (g + f )(21) 80
36. (f + g)(2) 11
37. (g + f )(0) 15
38. f(g(!6)) 21
39. f(g(0)) 29
4 40. g Q f Q 5 R R 21
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
83
Name
Class
Date
Chapter 6 Test (continued)
Form G
Find the inverse of each function. Is the inverse a function? 43. f(x) 5 !x 1 4 f21(x) 5 x2 2 4, x L 24; yes
41. f(x) 5 (x 1 2)2 2 4 42. f(x) 5 4x3 2 1 21 3 1 f (x) 5 w!x 1 4 2 2; no f21(x) 5 %x 1 4 ; yes 2 44. f(x) 5 3x 1 2 45. f(x) 5 x 2 5 2 f21(x) 5 x 2 3 ; yes
3
46. f(x) 5 !x 1 2 f21(x) 5 x3 2 2; yes
f21(x) 5 w!x 1 5; no
Graph. Find the domain and range of each function. 1 47. y 5 !x 2 1 1 2 48. y 5 2!x 1 3 2 1 49. y 5 2 !x 1 3 50. y 5 2!x 1 4 2 1 domain: x L 24; domain: x L 1; domain: x L 23; domain: x L 0; range: y K 21 range: y L 2 range: y K 21 range: y L 3 4
y
y
2 O
4
4 2 O 2
x 2
x
2
4
4
yx
y
O
x 2
4
4 2 O 2 4
Rewrite each function to make it easy to graph using transformations. Describe the graph. 3
51. y 5 !9x 2 63 1 4 y 5 3 !x 2 7 1 4; graph of y 5 3 !x shifted right 7 units and up 4 units
52. y 5 !8x 2 64 2 5 3
3
53. y 5 !227x 2 27 1 4 3
3
y 5 2 !x 2 8 2 5; graph of y 5 2 !x shifted right 8 units and down 5 units 54. y 5 !16x 2 32 y 5 4 !x 2 2; graph of y 5 !x shifted right 2 units
3
y 5 23 !x 1 1 1 4; graph of y 5 23 !x shifted left 1 units and up 4 units
55. The children’s park has become very popular since your club built new play equipment. Use the equation f 5 4!A to calculate the amount of fence f you
need to buy based on the area A of the playground. a. The park currently has an area of 8100 ft2. How many feet of fencing currently encloses the park? 360 ft b. Suppose you want to increase the fenced play area to four times its current area. If you can reuse the fencing already at the park, how much new fencing do you need to buy? 360 ft
Do you UNDERSTAND? 1
1
56. Writing Explain under what circumstances 2xn 5 (2x)n and provide an 1 1 example to justify your answer. n is an odd integer; answers may vary. Sample: 283 5 22 5 (28)3 3
57. Reasoning Graph y 5 !x and y 5 !x on the same coordinate grid. Notice 3 that for 0 , x , 1, the graph of y 5 !x lies below the graph of y 5 ! x but the opposite is true for x . 1. Explain why this is the case. Give an example. 1
Answers may vary. Sample: xn grows more rapidly (that is, as n increases) for 1 1 x R 1 and grows more slowly for x S 1; for example, Å64 5 18 R 14 5 3Å64 but 3
!64 5 8 S 4 5 !64.
Prentice Hall Gold Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
84
Name
Class
Date
Chapter 6 Quiz 1
Form K
Lessons 6–1 through 6–4 Do you know HOW? Find each real root. 1. !49 7
3
2. !0.36 0.6
3. !2125 –5
Simplify. Assume that all variables are positive. 3
4. "600x6y3 10x3y !6y
4
5. " 54xy5
6. " 64x4y8 4 2xy2 !4
3
3y "2xy2
Divide and simplify. 7.
3
"20x3 "5x 2x
8.
"56x4y
9.
3
"7x3y 3
2 !x
"32a7b2 "2a3b 4a2 !b
Simplify. 10. !7 1 3 !7 4 !7
11. !18 1 !32 7 !2
3
3
12. 2 !24 2 !81 3
!3
Write each expression in radical form. 3
1
13. x3
15. x1.5
14. x4 4
3
x"x
"x 3
!x
Write each expression in exponential form. 3
16. " 4x2 Q4x2R
18. "65x4y
17. !5ab
1 3
1 (5ab) 2
1
x 2(65y) 2
Do you UNDERSTAND? 19. Writing Explain when absolute value symbols are needed when you are n simplifying radical expressions. For radicals in the form "a m , if the index is even, use absolute value symbols. If the index is odd, you don’t need absolute value symbols for any . 20. An object is moving at a speed of A5 2 !3B mi/h. How long will it take the
object to travel 35 mi? 175 1 35 !3 22
h Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
85
Name
Class
Date
Chapter 6 Quiz 2
Form K
Lessons 6–5 through 6–8 Do you know HOW? Solve. Check for extraneous solutions. 1. 4 !x 2 2 5 2 x 5 1
2. !x 1 5 5 4 x 5 11
3. !5x 2 1 1 3 5 x x 5 10
4. !2 2 x 2 x 5 4 x 5 22
Let f (x) 5 x2 2 x and g (x) 5 2x 2 2 . Perform each function operation and then find the domain of the result. f f x 5. (f 1 g)(x) (f 1 g)(x) 5 x2 2 x 2 2; 6. a g b (x) a g b (x)5 2 ; all real numbers except x 5 21
all real numbers
Find the inverse of each function. Is the inverse a function? 3
8. y 5 (x 2 2)3 1 1 y 5 !x 2 1 1 2; yes
7. y 5 x2 2 3 y 5 6 "x 1 3 ; no
Graph each function. 2 9. y 5 3 !x
6
y
4 2 O
domain: x L 0 range: y L 0
3
10. y 5 2!8x 1 5
6
y
4 2
x
2 4 6
2 O
x
2
domain: all real numbers range: all real numbers
Do you UNDERSTAND? 11. Multiple Choice The graph of y 5 2!x is shifted 4 units up and 3 units right. Which equation represents the new graph? B
y 5 2!x 2 4 1 3
y 5 2!x 1 3 1 4
y 5 2!x 2 3 1 4
y 5 2!x 1 4 1 3
12. Writing Explain the relationship between the domain of a function and the range of the function’s inverse. They are equal
13. A spherical water tank holds 6000 ft3 of water. What is the diameter of the tank p to the nearest tenth of a foot? (Hint: V 5 6 d3 ) 22.5 ft
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
86
Name
Class
Date
Chapter 6 Test
Form K
Do you know HOW? Simplify each radical expression. Use absolute value symbols when needed. 3
1. "49x2y10 7»xy5…
5
2. " 264y9 24y3
3. " 243x15 3x3
5. "7x3 ? "14x 7x2 !2
6. 3" 4x3 ? " 8xy5
Multiply and simplify. 3
3
4. " 15 3 " 18 3
3 !10
Rationalize each denominator. Simplify your answer. !x !5x 1 !3 7. 8. 5 !3 3 !5
4
4
4
6xy !2y
3 ! 4 !2x
3
!2x2 x
9. 3
Multiply. 10. (7 1 !5)(1 1 !5) 12 1 8"5
11. (6 1 !10)2 46 1 2"10
12. (5 1 !3)(2 2 !3) 7 2 3 !3
Simplify each number. 2
3
14. 251.5 125
13. 273 9
15. 2 4
4
!8
Write each expression in simplest form. 3
16. ax2 b
22
1 x3
4
3 3
17. Q x 4 R
3 1 16 y 4
x
18. Q x 2 8y 4 R
x6
Solve. 19. !2x 1 1 5 5
x 5 12
1
3
20. (x 1 6) 4 5 8
x 5 10
21. Ax2 1 13B 2 5 7 x 5 6 and x 5 26
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
87
Name
Class
Date
Chapter 6 Test (continued)
Form K
Let f (x) 5 "x 1 3 and g (x) 5 4 2 "x. Perform each function operation and then find the domain. 22. ( f 2g) (x) (f 2 g)( x) 5 2"x 2 1;
23. ( f ? g)(x) (f ? g)( x) 5 "x 2 x 1 12; all real numbers L 0
all real numbers L 0
Let f (x) 5 3x 1 1 and g (x) 5 x2 1 2. Find each value or expression. 24. ( f + g)(2) 19
25. (g + f )(23) 66
Graph each relation and its inverse. 26. y 5 x 1 4
4 2 4 2 O 2
27. y 5 x2 2 2
y
yx4
4 2
yx4
4x
2
y
y x2 2
4 2 O 2
x 2
4
4 y 兹x 2
4
Rewrite each function to make it easy to graph using transformations of its parent function. Describe the graph. 3
28. y 5 "16x 2 32 y 5 4"x 2 2 ;
29. y 5 "8x 1 3
3
y 5 2" x 1 3; 3
vertical stretch of y 5 "x by a factor of
vertical stretch of y 5 " x by a factor of
4 and translation 2 units right
3 and translation 3 units up
Do you UNDERSTAND? 30. Error Analysis Explain the error in this simplification of radical expressions. 3 What is the correct simplification? !2 ? ! 8 5 !2(8) 5 !16 5 4
The product property does not apply to different indexes; 2 !2
6
6
31. Reasoning Show that " x3 5 !x by rewriting " x3 in exponential form. 6
"x 3 5
3 x6
5
1 x2
5 !x
32. A store is having a sale with a 15% discount on all items. In addition, employees get a
$20 discount on purchases of $100 or greater. Will an employee get a better deal if the $20 discount is applied first or if the 15% discount is applied first to their purchase of $100? The employee will pay less if the 15% discount is applied first.
Prentice Hall Foundations Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
88
Name
Class
Date
Chapter 6 Performance Tasks
Give complete answers. Task 1 a. Write a product of two square roots so that the answer, when simplified
is 12x3y2. Show how your product simplifies to give the correct answer. b. Write a quotient of two cube roots so that the answer, when simplified, is
Show how your quotient simplifies to give the correct answer.
3a2 . 4b3
c. Write a product of the form Q a 1 !b R Q a 2 !b R so that the answer, when
simplified, is 59. Show how your product simplifies to give the correct answer. [4] Check students’ work. All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found products and quotient correctly but followed through the process incorrectly using incorrect simplification. [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student understood that squaring, cubing or multiplying was involved but was unable to correctly find the products or quotient, or to simplify them. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown
Task 2 a. Find a radical equation of the form !ax 1 b 5 x 1 c so that one solution is
extraneous. Show the steps in solving the equation. b. Is there a value for h that makes it possible for the equation !x 1 h 1 5 5 0
to have any real number solutions? Explain. c. Explain the relationship between the solutions to the equation
!x 2 3 2 2 5 0 and the graph of the function y 5 !x 2 3 2 2. [4] Check students’ work. All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found parts (a) and (b) correctly but could not explain (c) OR could not show steps in (a) OR could not explain (b). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student know to square each side of the equation, but could not complete the solution. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
89
Name
Class
Date
Chapter 6 Performance Tasks (continued)
Let f (x) 5 x2 1 x 2 12 and g(x) 5 x 2 2. Answer each of the following questions. Task 3 g(x)
x22 ; all real numbers a. Find f(x) and its domain. Explain how you determined the domain. 2 x 1 x 2 12 except 3 and 24 b. Find (g + f)(x) and (f + g)(x). Are they equal? x2 1 x 2 14; x2 2 3x 2 10; no
c. For what types of functions will (g + f)(x) and (f + g)(x) both equal x? Explain. when f and g are [4] All parts of Task completed correctly with work shown OR used correct inverses process with minor computational errors. [3] Student found all parts correctly but could not explain (a) OR could not explain (c) OR could not correctly find the domain for (a). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student found part (a) but could not compose functions for parts (b) and (c). [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Give complete answers. Task 4 a. Find the inverse of f(x) 5 !x 2 2 1 5. Show all steps in the process. What
is the domain of
f21 ? f 21(x) 5 (x 2 5)2 + 2; domain: x L 5
b. Choose a value for a and use the inverse to find Q f + f21 R (a) and
Q f21 + f R (a) for the value you chose. What can you conclude about Q f + f21 R (a) and Q f21 + f R (a)? (f ° f21)(a) 5 (f 21 ° f)(a) 5 a c. Graph f and
6
y
4
x O
on the same axes. What relationships do you see between the two graphs? The graphs are a reflection of each other across the line y 5 x.
[4] All parts of Task completed correctly with work shown OR used correct process with minor computational errors. [3] Student found parts (a) and (b) correctly but could not describe the relationships between the graphs OR could not draw conclusions in part (b). [2] Correct answer with no work shown OR student only able to complete part of Task. [1] Student found the inverse of f(x) but could not draw conclusions in part (b) and could not graph the functions. [0] No attempt was made to solve this problem OR answer is incorrect with no work shown.
Prentice Hall Algebra 2 • Teaching Resources
90
f1
2
f21
Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
f
2
4
6
Name
Class
Date
Chapter 6 Cumulative Review
Multiple Choice For Exercises 1−12, choose the correct letter. 1. What is an equation for this graph? B
y 5 (x 1 3)2 1 1
y 5 (x 2 1)2 2 3
y 5 (x 2 3)2 1 1
y 5 (x 2 1)2 1 3
7 6 5 4 3 2 1
y
x
O 1 2 3 4 5 6 7
2. Simplify
3 42
. I 3 2
24 3. Solve the system. e
6
8
y 5 x2 2 3x 2 8 C y5x14
(22, 2), (2, 210)
(22, 2), (6, 10)
(21, 24), (1, 5)
(2, 6), (6, 10)
4. Which of the following polynomials has roots 0, 1, and 2? G
p(x) 5 x2 1 x 1 2
p(x) 5 x3 2 2x 1 1
p(x) 5 x3 2 3x2 1 2x
p(x) 5 x2 1 2x
5. Complete the square. 3x2 2 2x 1
1 9
uB
1 3
1
3
6. Let f(t) 5 t2 1 5t 2 2 and h(t) 5 t2 2 2t 2 6. What is the function for h(t) 1 f(t)? F
2t2 1 3t 2 8
4t2 1 t 2 8
22t2 1 3t 2 2
2t2 1 t 2 8
213 1 11i
215 2 2i
5 4 i !29 2
25 4 i !21 2
7. Simplify. (25 1 2i)(3 2 i) C
22 1 i
217 1 i
8. What is the solution to x2 2 5x 1 1 5 0? F
5 4 !21 2
25 4 !29 2
9. If h(x) 5 2x2 1 x 2 5 and g(x) 5 24x 2 1, what is the value of h(1) 2 g(3)? C -15
-11
11
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
91
15
Name
Class
Date
Chapter 6 Cumulative Review (continued)
10. Solve the system. e
y 5 2x2 1 x 1 12 G y 5 x2 1 3x
(24, 4), (0, 12)
(23, 0), (0, 12)
(23, 0), (2, 10)
(21, 22), (0, 12)
11. Which of the following relations defines y as a function of x? C
x2 1 y2 5 6 6 2 2i 12. Simplify. 1 1 3i F
22i
y 5 4 !4 2 x
y 5 x2 2 3
x 5 y2
6 2 23i
6 8 5 1 5i
6 8 5 2 5i
Short Response For Exercises 13 and 14, let f(x) 5 x2 1 2x 2 3 and g(x) 5 4x 2 1. 13. Simplify each expression. a. g(x 1 2) 4x 1 7
b. f(x 1 2) x2 1 6x 1 5 6
14. Find each value. a. (g + f )(0) 213
b. (f + g)(0) 24
2 O
y
x 6
10
2x2
y, 2 2x 1 3 15. Solve by graphing. e 2 y . x 2 x 2 12 16. To find the time t, in seconds, it takes an object to fall h meters, use the h equation t 5 Å4.9 . A croissant dropped from the top of the Eiffel Tower takes 8.13 s to reach the ground. How tall is the Eiffel Tower? 324 m
Simplify each expression. Assume that all variables are positive. 4
125a15b7 3 625a16b4 17. a b 16 28a3b4
18. Q 4 2 5 !3 R Q 4 1 5 !3 R
259
Extended Response 19. Writing Explain how you can obtain the solutions to a system of equations by graphing. 19. [4] Answers may vary. Sample: Graph both equations on the same grid. If the graphs do not intersect, then the system has no solution. If the graphs intersect in one or more points, then the intersection point(s) are the solution(s) of the system. [3] Explanation shows understanding of the concepts with some minor errors. [2] Explanation contains minor errors. [1] Explanation contains major errors and lacks detail. [0] Explanation is missing. 20. Open-Ended Write the equation of a parabola with vertex at (22, 3). 20. [4] Answers may vary. Sample: f(x) 5 (x 1 2)2 1 3. [3] Equation has minor errors. [2] Equation has major errors. [1] Equation is incomplete and the given answer has errors. [0] Equation is missing. Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
92
TEACHER INSTRUCTIONS
Chapter 6 Project Teacher Notes: Swing Time
About the Project The Chapter Project gives students an opportunity to conduct experiments involving a real-world application of physics and mathematics. Students solve a formula for a given variable to write the formula in a more useful form, then use the formula to determine the periods of pendulums.
Introducing the Project • Ask students if they have ever used a pendulum, or a swing-like motion. Remind them that the motion of a playground swing is similar to a pendulum’s motion. • Have students speculate as to whether a homemade pendulum could continue to swing forever, or if it would eventually stop swinging. Encourage them to discuss what might cause a pendulum to stop swinging.
Activity 1: Constructing Students use strings, coins, and binder clips to construct simple pendulums.
Activity 2: Investigating Students perform experiments to time the swings of their pendulums and record their observations in charts.
Activity 3: Analyzing Students solve a formula for a given variable, then use the formula to find the theoretical periods of their pendulums. They analyze their data and determine why their experimental results might differ from their theoretical results.
Finishing the Project You may wish to plan a project day on which students share their completed projects. Encourage students to explain their processes as well as their results. • Have students review their data and their calculations of the periods. • Ask groups to share their insights that resulted from completing the project, such as any shortcuts they found for using the formula or calculating the periods. SOURCES: Basic Physics: A Self-Teaching Guide, Second edition, p. 104, by Karl F. Kahn, 1996, John Wiley & Sons, Inc.; Physics, p. 242, by John D. Cutnell and Kenneth W. Johnson, 1989, John Wiley & Sons, Inc.
Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
93
Name
Class
Date
Chapter 6 Project: Swing Time
Beginning the Chapter Project Galileo observed a swinging lantern and made an important discovery about the timing of a pendulum’s swing. A Dutch man named Christiaan Huygens discovered the relationship between the length of a pendulum and the time it takes to make a complete swing, which led to the use of pendulums in clock making. You will construct pendulums using strings and weights and use your pendulums to investigate whether the length of the string or the amount of weight attached to a pendulum affects the time it takes the pendulum to make one full swing.
List of Materials • Calculator
• Metric ruler or measuring tape
• Thread or thin string
• Binder clips (2 medium)
• Coins (3 quarters, 3 nickels, or 3 pennies)
• Stopwatch
Activities Activity 1: Constructing To construct a simple pendulum, tie a medium binder clip to the end of a piece of string. The binder clip will be used to hold one or more coins for the experiments in Activity 2. The weight on the end of the string, which includes the binder clip and the coin(s) it holds, is called the pendulum bob. The period of a pendulum is the time it takes for the pendulum to complete one full swing (back and forth). Activity 2: Investigating Experiment 1 Tie the free end of the string of the pendulum to a stable object. Do this in such a way that neither the string nor the bob touch another object when the pendulum is swung. Insert one coin in the binder clip. Measure the length of the string (in centimeters) from the point where it is attached to the stable object to the center of the bob. Record this length. Three times, pull the pendulum back to an angle of about 20° and let it go. For each trial, use a stopwatch to record the number of seconds it takes for the pendulum to complete 10 full swings. Record each time in the first column of the table provided on the next page. Next, find and record the average of the three times you listed. Finally, divide the average time by 10 to determine the period of the pendulum. Repeat the procedure using two coins, then using three coins, recording the data in the second and third columns, respectively. Does it appear that the weight of the bob affected the period of the pendulum? What factors other than the weight might affect the period of the pendulum? Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
94
Name
Class
Date
Chapter 6 Project: Swing Time (continued)
1 coin
2 coins
3 coins
Trial 1 Trial 2 Trial 3 Average time to complete 10 full swings Period of pendulum
Experiment 2 Cut a second string that is half the length of the original string. Repeat Experiment 1. Record data in a table. Does it appear that the pendulum string length affects its period? Explain. Activity 3: Analyzing 2
The formula / 5 980t2 represents the length O (in centimeters) of a simple 4p pendulum with a period of t seconds. (In this formula, the acceleration due to gravity is given as 980 cm/s2.) • Solve for t. According to the formula, how does changing the weight of the bob affect the period of a pendulum? • Use the formula to find the theoretical period for each pendulum. Record your experimental and theoretical periods for each. Length of Pendulum
Experimental Period
Theoretical Period
Experiment 1 Experiment 2
Do your experimental results give the same period as the theretical models? What factors do you think would for any differences? Explain your observations.
Finishing the Project Prepare a presentation for the class describing your results. Your presentation should include a chart showing your experimental and theoretical results.
Reflect and Revise When you are sure your data are accurate, decide if your presentation is complete, clear, and convincing. If needed, make changes to improve your presentation.
Extending the Project Research the use of clock pendulums. Find out how a pendulum keeps time. Research periods of the pendulums used in different clock types. Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
95
Name
Class
Date
Chapter 6 Project Manager: Swing Time
Getting Started Read the project. As you work on the project, you will need a calculator and materials on which you can record your results and make calculations. Keep all of your work for the project in a folder, along with this Project Manager. Checklist
Suggestions
☐ Activity 1: constructing a pendulum
☐ Use the lightest thread or string possible.
☐ Activity 2: determining the period
☐ Have one student swing the pendulum while another student keeps time.
☐ Activity 3: comparing experimental and theoretical periods
☐ Isolate t, then take the square root of each side of the equation. Substitute the string lengths into the new equation.
☐ pendulum experiment
☐ How would your results change if your pendulum were not able to swing freely, that is without with any other object? How would your results change if you pulled the pendulum back to an angle of 60°? What other changes would affect your results?
Scoring Rubric 4
Your experimental results are reasonable. Calculations are correct. Explanations are thorough and well thought out. Data, calculations, and conclusions are neatly presented.
3
Your experimental results are reasonable. Calculations are mostly correct with some minor errors. Explanations lack detail and accuracy. Data, calculations, and conclusions are not well organized.
2
Your experimental results are not reasonable. Calculations and explanations contain errors. Data, calculations, and conclusions are unorganized and lack detail.
1
Major concepts are misunderstood. Project satisfies few of the requirements and shows poor organization and effort.
0
Major elements of the project are incomplete or missing.
Your Evaluation of Project Evaluate your work, based on the Scoring Rubric.
Teacher’s Evaluation of Project Prentice Hall Algebra 2 • Teaching Resources Copyright © by Pearson Education, Inc., or its s. All Rights Reserved.
96